什么是递归

原创已于 2024-09-26 01:25:37 修改 · 2.1k 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#golang #leetcode

于 2024-09-21 14:05:49 首次发布

二叉树专栏收录该内容

34 篇文章

订阅专栏

文章目录

生活中的递归小例子
递归递归，先有递再有归
递归经典示例一：阶乘
递归经典示例二：青蛙跳台阶问题
重要提示（青蛙跳台阶类别二叉树遍历左右子树）
总结

生活中的递归小例子

递归就像我们查字典的时候，当查找一个词时，发现它的解释中某个词仍然不懂，于是开始查找第二个词
在这里插入图片描述

像千钧一发这个词的解释中 千钧一词不懂，于是开始查找千钧的意思。在千钧的解释中一石(dan)为四钧 ，一石这个词还是不懂，于是继续查找 一石，到这里我们明白了一石指的是120斤

就像这样我们一直查找，直到有一个词的解释完全明白为止

那么我们就可以开始后退，一石指120斤，那么4钧为1石，则1钧为30斤
则千钧为3万斤

到此我们就彻底明白了千钧一发的意思

递归递归，先有递再有归

递的意思就是将问题拆解成子问题来解决，子问题再拆解为子问题，直到被拆解的问题无需再拆解为更细的子问题为止

就像在字典中一直查找不明白的词语的情况

归的意思是最小的子问题得到解决了，那么它的上一层也会有由于它的解决而被解决，上一层的子问题解决了，那么上上层的问题自然也就解决了，一直到开始的问题被解决

在编程中，递归简单来说，就是如果在函数中存在着调用函数本身的情况，这种就可以称为递归

递归经典示例一：阶乘

可以看到在 factorial 函数中，存在着一个 factorial 函数的调用，所以这个函数就是递归函数，factorial 函数我们简写下，改为f，（C语言版）
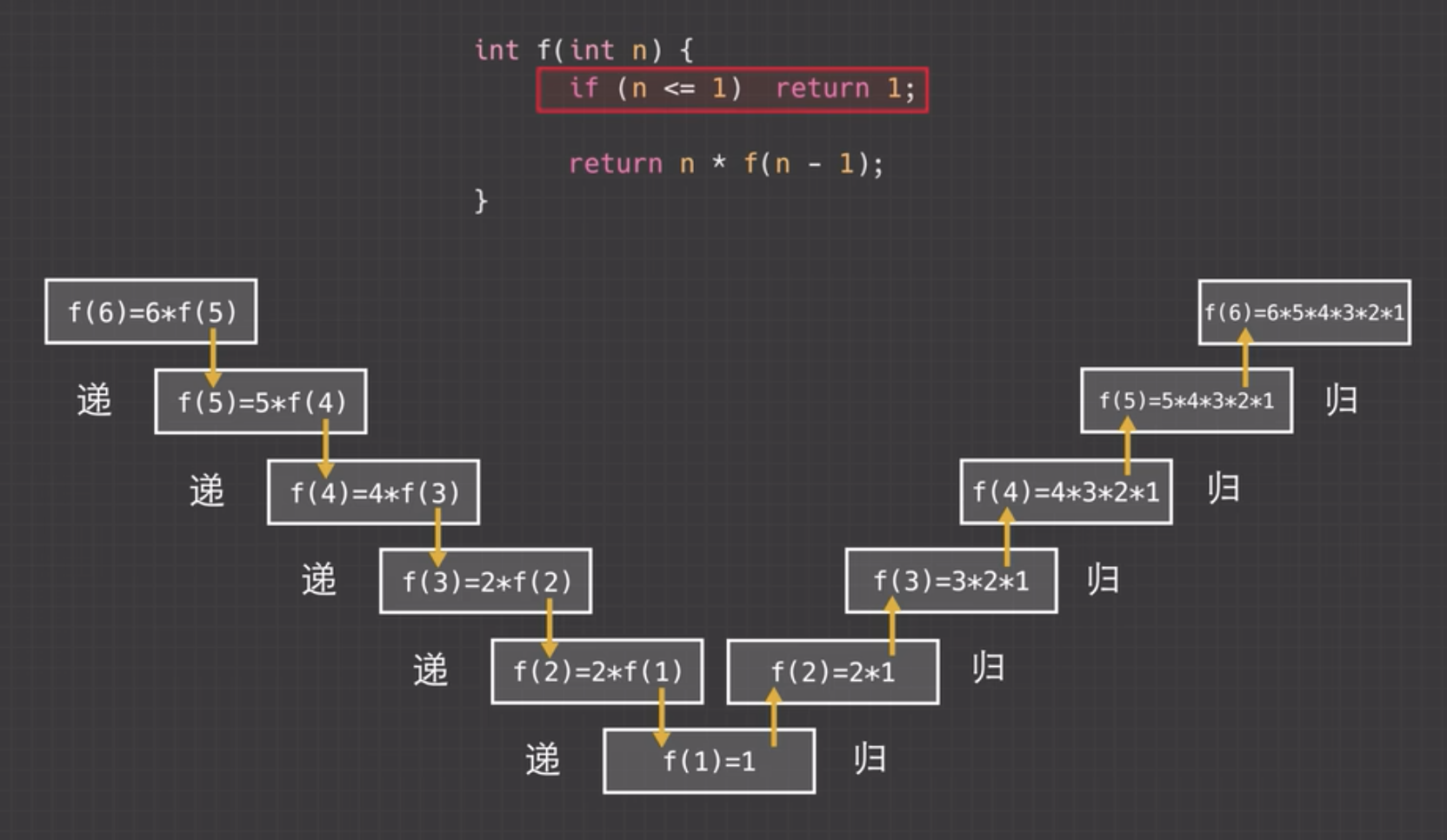
在这里插入图片描述

我们以阶层f(6) 为例，看下它的递和归

进行递

求解问题f(6），n为6，n大于1，则return n * f(n-1)，当前n为6，则 f(6) = 6 * f(5)

所以 f(6) 被拆解为 f(5) 的子问题

同理 f(5) = 5 * f(4) 也需要进一步拆解
f(4) = 4 * f(3)
f(3) = 3 * f(2)
f(2) = 2 * f(1)

当n等于1时f(1) = 1，到这时 f(1) 的问题解决了，无法继续往下递了

进行归
既然f(1)解决了，那么 f(2) 只依赖于f(1) 所以f(2)问题也可以解决了

f(3) 依赖 f(2)的结果，f(2)解决了那么f(3)也可以解决了

同理 f(4)、f(5)、f(6)都可以解决

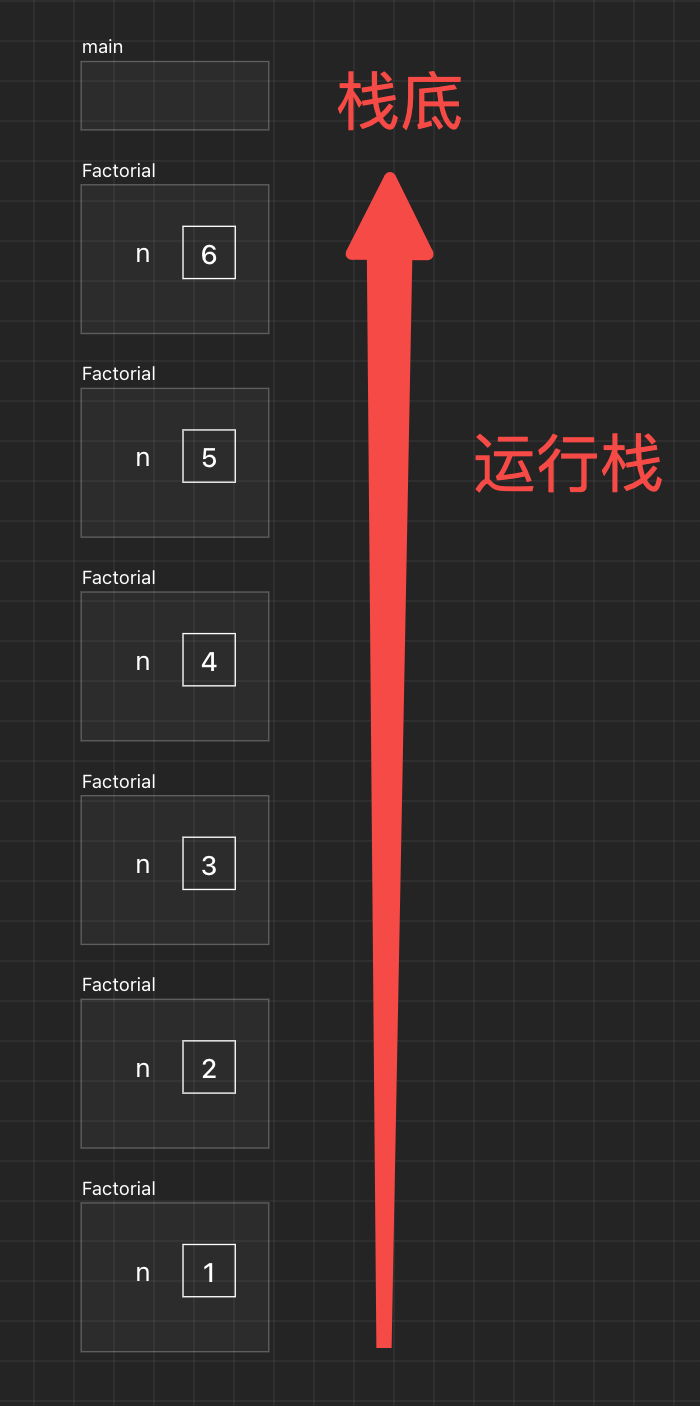
在这里插入图片描述

系统运行栈如下：

递就是不断的入栈，归则是不断的出栈
在这里插入图片描述

所以递归的本质就是把问题拆分成具有相同解决思路的子问题，直到最后被拆解的子问题再也不能拆分，解决了最小粒度可求解的子问题后，在归的过程中自然而然地就解决了最开始的问题

递归经典示例二：青蛙跳台阶问题

一只青蛙可以一次跳1级台阶或者一次跳2级台阶，跳上第1级台阶只有1种跳法，直接跳1级即可，跳上第2级台阶有两种跳法，每次跳1级，跳两次；或者1次就跳两级

问：要跳上第n级台阶有多少种跳法呢？

仔细看题目，一只青蛙一次只能跳1级或者2级台阶

自上而下的思考，也就是说如果要跳到n级台阶只能从n-1或 n-2级开始跳

所以问题就转化为跳上 n-1 和n-2级台阶的跳法了，如果f(n) 代表跳到第n级台阶的跳法，那么从以上分析可得 f(n)的函数为 f(n) = f(n -1) + f(n -2)

显然这就是我们要找的问题和子问题的关系

进行递操作

而显然当 n = 1和n = 2时，即跳到1， 2 阶台阶时是问题的最终解(递归的终止条件），也是已知解，n=1时有一种跳法，n=2时有两种跳法

那么跳到第6层时有多少种跳法，可以看作求解问题 f(6)

在这里插入图片描述

n = 6时，返回f(5) + f(4)那么 f(6)被拆解为f(5)和f(4)的子问题

继续递下去，求解 f(5) 则需要知道 f(4)和f(3)

求解f(4)需要知道 f(3) 和 f(2)

求解 f(3) 需要知道 f(2) 和 f(1)

f(2)已知等于2

f(1)已知等于1

问题已经得到最小化，无法继续递下去了

进行归操作

f(3) = f(2) + f(1)，f(2)有2种跳法f(1)有1种，所以 f(3) = 2 + 1 = 3
在这里插入图片描述

f(4)=f(3)+f(2)，f(3)有3种，f(2)有2种，所以f(4)有5种跳法

在这里插入图片描述

f(5)=f(4)+f(3)，f(4)有5种，f(3)有3种，所以f(5)有8种跳法

在这里插入图片描述

f(6)=f(5)+f(4)，f(5)有8种，f(4)有5种，所以f(6)有13种。也就是说青蛙跳上第6阶有13种不同跳法

在这里插入图片描述

注意：代码实际执行f(6)=f(5)+f(4)的时候，不是同时将f(5)和f(4)计算出来的，而是先计算出f(5) = 8,回归到f(6)那层时，得到f(6) = 8 + f(4)，此时才会去计算该表达式中的f(4)，最终得到f(6)=8+5=13。可以发现计算f(6)=f(5)+f(4)表达式时，f(4)其实计算了两次，一次是得出f(5)时，f(5)=f(4)+f(3)，第二次是f(6)=f(5)+f(4)中的f(4)。而f(3)实际则是被计算过三次的（一次是为了回归出f(6)=f(5)+f(4)表达式中的f(5), 一次是为了回归出f(5)=f(4)+f(3)，一次是为了回归出f(6)=f(5)+f(4)表达式中的f(4))，如下图：
在这里插入图片描述

对应到二叉树就是下图：
在这里插入图片描述

总结：写递归代码的关键就是找到如何将大问题分解为小问题的规律，然后再推敲终止条件，有了递归终止条件和子问题，至于子问题的解，让它自己去套娃从更小的子问题得出解，它总会走到递归终止条件处找到答案再一步一步回归回来的

重要提示（青蛙跳台阶类别二叉树遍历左右子树）

我想这里的青蛙跳台阶问题，大家可能一看就懂了，但面对二叉树的时候又懵了，比如二叉树求最大深度和最小深度的题目

104. 二叉树的最大深度(包括N叉树的最大深度）

111. 二叉树的最小深度

其中就会出现这样的代码

最大深度

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    // 这里实际是后续遍历（左右根），不过用一行写了
    return max(maxDepth(root.Left),maxDepth(root.Right)) + 1
}

func max(a,b int) int {
    if a > b {
        return a
    }

    return b
}

对于 return max(maxDepth(root.Left),maxDepth(root.Right)) + 1这一行代码，很多同学都是一看就懂，一写就废，原因就是没有深入理解这行代码具体的执行流程是怎么样的。

实际这行代码和青蛙跳台阶的思路几乎是一致的，青蛙跳台阶是递归求f(n-1)和f(n-2)，然后两个递归的结果相加，而二叉树则是递归左子树maxDepth(root.Left)和右子树maxDepth(root.Right)，最后取较大的结果+1。

它们都是先一路递归下去，达到递归终止条件后，得到最小问题的解，然后回归回来，得到上层问题的解。当然，要注意，同层的递归栈中，是maxDepth(root.Left)全部递归并回归回来后，才继续去递归同层的maxDepth(root.Right)的，等maxDepth(root.Right)也回归到该层时，才执行当前层的 max(maxDepth(root.Left),maxDepth(root.Right)) + 1。每一层都是这个递归和回归逻辑。建议大家画画图深入理解一下，有助于做后续的二叉树和回溯专题题目。

总结

这个总结其实是自己写了不少二叉树题目后，返回来看这篇文章的时候写的。这里写下来是觉得写在这里比较合适，不过当看了不少二叉树题目的解法和思路后，再回头来看这个总结会更感同身受。

记得高中物理中有一个公式
$\begin{rcases} x = v_0t+1/2at^2 \\ v = v_0+at \end{rcases}⇒v²-v_0²=2ax$
通过前两个公式可以推出右边的公式，开始学习的时候是需要去理解去推导的，但是熟悉后，就直接使用，不用临时推导了，尤其是考试的时候，知道这个推导得到的公式一定是对的，难道在争分夺秒的考场上还去推导一番？
递归也是一样，深刻理解了底层递归，就可以直接写代码了，如爬楼梯很好理解，大家写完 $f (n) = f (n - 1) + f (n - 2)$ 后大部分同学都很自信他是对的，不会去细细的琢磨他是如何递归到最底层并将结果一步一步回归回来的。
二叉树左右子树道理其实是一样的，到达最底层得到最小解，然后一层一层再左右子树往上归，直到归到根节点拿到最终结果，心里有这个递和归的路径图就好，熟练之后，写题时在确定了递归终止条件后，可以大胆一点的直接一步递归左右子树，不必又去细致的考虑具体如何递以及如何归的（当然心里还是要有数，以及初学的时候可以画图大致模拟一下加深理解和验证是否思路正确）

二叉树递归的一些思路总结：

路径之类的都是从根节点开始，适合前序遍历。
如
226. 翻转二叉树之多种解法(递归法、深度优先（迭代法）、广度优先【层序遍历】）
257. 二叉树的所有路径（回溯详解）
112. 路径总和
需要递归左右子树，然后对左右子树的结果进行比较或相加等操作的，说明是递归到最深处，再把左右子树的结果层层回归到根节点得出整棵树的解，相当于最后才处理根节点，这种后续遍历。
如：
104. 二叉树的最大深度(包括N叉树的最大深度）
110. 平衡二叉树
 222. 完全二叉树的节点个数
 101. 对称二叉树(共含三道leetcode题）

再举一个例子，大家看下面对二叉树的前序遍历代码，估计大家都会觉得非常好理解，毕竟是最基本的遍历，学习二叉树的最开始就会学习这个遍历，递归的遍历收集每一个节点的值罢了。既然如此，大家为啥面对其他二叉树递归的题目时，却好像显得无从下手，或者觉得那些递归难以理解呢？

实际上类比一下就好啦，那些二叉树的题目大部分就是把节点的处理逻辑和递归终止逻辑变了而已。比如下面的前序遍历代码，我们要求只有节点的Val为偶数时才收集，是不是立马就可以修改一下代码得出符合要求的代码，因为就是改下节点的处理逻辑【收集结果时加个是否为偶数的条件】罢了。再或者我们要求只收集所有非叶子节点的Val，是不是也很容易就想到了，改下递归终止条件，当前节点的左右孩子为空就可以return了，因为他是叶子节点，不需要继续往后遍历了。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func preorderTraversal(root *TreeNode) []int {
    if root == nil {
        return []int{}
    }

    res := make([]int,0)
    // 注意res传的是指针，因为函数内部res可能扩容，所以用指针保证还能拿到原切片
    traversal(root,&res)

    return res
}

func traversal(root *TreeNode,res *[]int){
    if root == nil {
        return 
    }

    *res = append(*res,root.Val)
    traversal(root.Left,res)
    traversal(root.Right,res)
}