通过两道题深入理解二叉树递归-优快云博客

文章目录

注：递归和回溯相辅相成

当递归一进来就是做某个操作，比如改变结果列表，或者变更遍历路径上的结果时，此时一般使用前序遍历模式，因为前序才是一进来就可以访问根节点（根左右）。且此时的递归模式和回溯法的原理是完全一样的，即一层一层寻找进去，将上层临时结果带到下层，然后在一层一层回溯回来，回归到上层前，临时结果也回退回上层的结果，而每一层都可能有多个选择【当然，二叉树一层就两个选择，左或者右】，此时继续选择另一路径，如开始选的左，那此时回溯到此层时将选右，左右都选过执行完后，就回到上层去了。
当递归一进来就是开始递归，如遍历左孩子，那么一般是遍历左边到头了，再回溯回来，如最基础的中序遍历和后序遍历，其中后序遍历一般用于最后才处理根节点的情况，如力扣104. 二叉树的最大深度，最大深度就是先得到左子树与右子树的最大深度，根节点的最大深度则为左子树或右子树的最大深度+1（即加上根节点那层），就是根节点到叶子节点的最大深度。

剑指 Offer 34. 二叉树中和为某一值的路径

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

示例:
给定如下二叉树，以及目标和 sum = 22，

			  5
             / \
            4   8
           /   / \
          11  13  4
         /  \    / \
        7    2  5   1

[
   [5,4,11,2],
   [5,8,4,5]
]

提示：

节点总数 <= 10000

注意：本题与主站 113 题相同：113. 路径总和 II

解题思路

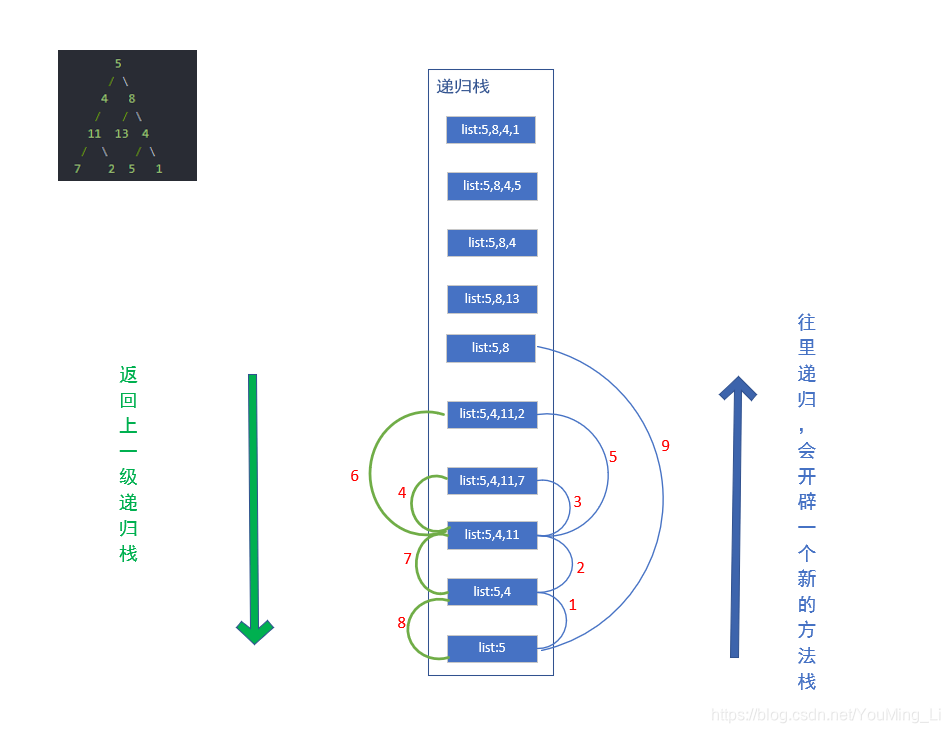
题中所指的路径是从根节点出发到叶节点，也就是说路径总是以根节点为起始点，以叶子节点为终点，因此我们首先要遍历根节点。纵观树的前、中、后序三种遍历方式中，只有前序遍历是首先访问根节点的，所以我们应选择前序遍历。

当用前序遍历的方式访问到某一节点时，我们把该节点添加到路径list中，并更新sum的值，如果该节点是叶子节点，且sum此时为0了，说明当前的路径符合要求，我们当前路径加入到res中。如果当前节点不是叶节点，则继续访问他的子节点。当前节点访问结束后，递归函数会自动回到他的父节点（而不要使用return返回，代码中有注释详解说明原因）。我们需要进行现场恢复。

递归简要流程如下:对应着前序遍历
在这里插入图片描述

Java代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
	//设置成成员变量，避免每次递归的参数传递
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        //深度优先遍历
        if(root == null) return res;
        dfs(root,sum,new ArrayList<>());
        return res;
    }

    public void dfs(TreeNode root,int sum,List<Integer> list){
         list.add(root.val);
         sum -= root.val;
        if(root.left == null && root.right == null && sum == 0){
            res.add(new ArrayList<>(list));//一定要注意这里加的是副本
            //return ;//此处不能写return 因为还需要执行后面的两个dfs和list.remove语句，
            //这样才能执行到list.remove,把叶子节点删掉，从而还原回上一级栈的list
        }
       
        if(root.left != null) dfs(root.left,sum,list);
        if(root.right != null) dfs(root.right,sum,list);
        list.remove(list.size()-1);//回溯时还原为上级运行栈的list
        //sum无需还原，因为sum是值传递，实参本身就没变，变的是形参
    }
}

在这里插入图片描述

Go代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func pathSum(root *TreeNode, targetSum int) [][]int {
    if root == nil {
        return [][]int{}
    }

    //深度优先遍历
    res := make([][]int,0)
    curList := make([]int,0)
    dfs(root,&res,&curList,targetSum)
    
    return res
}

func dfs(root *TreeNode,res *[][]int,curList *[]int,targetSum int) {
    *curList = append(*curList,root.Val)
    targetSum -= root.Val
    if root.Left == nil && root.Right == nil && targetSum == 0 {
        // 一定要注意这里加的是副本 以及 学习这里添加列表副本的技巧
        *res = append(*res,append([]int(nil),*curList...))
        //return //此处不能写return 因为还需要执行后面的两个dfs和还原语句，
        //这样才能执行到*curList = (*curList)[0:len(*curList) - 1],把叶子节点删掉
        // 从而还原回上一级栈的curList
    }

    if root.Left != nil {
        dfs(root.Left,res,curList,targetSum)
    }
    if root.Right != nil {
        dfs(root.Right,res,curList,targetSum)
    }

    //回溯时还原为上级运行栈的curList
    //targetSum无需还原，因为targetSum是值传递，实参本身就没变，变的是形参
    *curList = (*curList)[0:len(*curList) - 1]
}

在这里插入图片描述

LeetCode 257. 二叉树的所有路径

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例:

输入:

输出: ["1->2->5", "1->3"]

解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3

解题思路

与上同。唯一要注意的就是本段代码中的最后那两行注释。事实上，即使那里写了s = s.substring(0,s.length() - 1),代码完全正确，道理还是那两行注释。
记住一句话，当我们觉得一个String对象被改变的时候，底层实际是生成了一个新的String对象。原始的String对象并没有被改变，只是变量改变了指向而已,即让变量指向了新建的String对象。

前序遍历以及回溯的过程如图：

回溯和递归中回归的区别：
回溯：因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。
回归：下层函数栈执行完成后，回归到上层函数栈来

实际上，回溯和回归都是伴随递归出现的，只是回溯比回归多了一个路径回退的操作。

在这里插入图片描述

Java代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    
    private List<String> res = new ArrayList<>();

    public List<String> binaryTreePaths(TreeNode root) {
            if(root == null) return res;
            dfs(root,"");
            return res;
    }

    private void dfs(TreeNode root,String s){
        s += root.val;
        if(root.left == null && root.right == null){
            res.add(s);
        }
        s += "->";
        if(root.left != null) dfs(root.left,s);
        if(root.right != null) dfs(root.right,s);
        //由于s的加法操作产生的是副本，即本级栈的s指向了生成的副本，但上级栈的s也即传进来的实参,并没有改变指向
        //故不会影响上一级运行栈中的s,因此此处无需还原s，它本身在这一级栈就没变,变的是这一级栈s的指向
    }
}

在这里插入图片描述

Go代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func binaryTreePaths(root *TreeNode) []string {
    if root == nil {
        return []string{}
    }

    res := make([]string,0)
    str := fmt.Sprintf("%d",root.Val)
    dfs(root,&res,str)

    return res
}

func dfs(root *TreeNode,res *[]string,str string) {
    
    if root.Left == nil && root.Right == nil {
        *res = append(*res,str)
    }

    if root.Left != nil {
        dfs(root.Left,res,str + "->" + fmt.Sprintf("%d",root.Left.Val))
    }

    if root.Right != nil {
        dfs(root.Right,res,str + "->" + fmt.Sprintf("%d",root.Right.Val))
    }
}

在这里插入图片描述