如何用Matlab将二维数据点绕Z轴即（0,0）旋转

在Matlab中键入以下代码：

clear 

clc

x=[0 1 1 0 0];

y=[0 0 1 1 0];

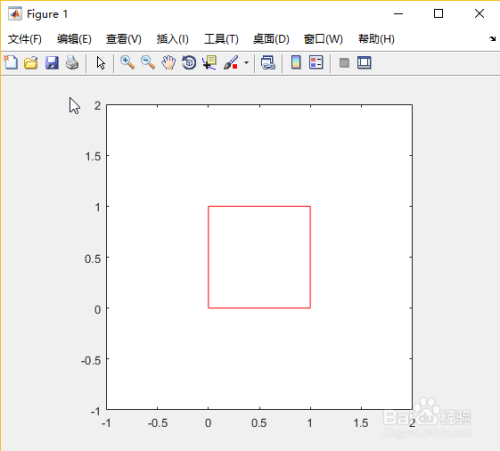
plot(x,y,'r');%绘制正方形

hold on

axis equal%将两坐标设为相等

axis([-1 2 -1 2])%设置显示范围

所得结果如图所示。

 

顺时针旋转图形，其旋转矩阵为M：

M=[cos(pi/6)   sin(pi/6);

   -sin(pi/6)   cos(pi/6);];

R1=[x;y;];

R2=M*R1;%旋转后坐标

plot(R2(1,:),R2(2,:),'b')%绘制旋转后图形

结果如图所示。