K-Means 聚类
学习目标
本课程将详细介绍K-Means聚类算法的工作原理、掌握数据预处理和探索性数据分析方法、应用 K-Means聚类算法、评估聚类结果以及理解数据可视化在聚类分析中的应用。
相关知识点
- K-Means 聚类
学习内容
1 K-Means 聚类
1.1 算法的工作原理
K-Means聚类算法通过迭代优化来产生最终结果。算法的输入是聚类的数量KΚK 和数据集。数据集是每个数据点的特征集合。算法从 KΚK个聚类中心的初始估计值开始,这些初始值可以是随机生成的,也可以是从数据集中随机选择的。然后,算法在两个步骤之间进行迭代:
数据分配步骤:每个聚类中心定义了一个聚类。在这个步骤中,每个数据点根据平方欧几里得距离被分配到最近的聚类中心。更正式地说,如果 cic_ici 是集合CCC 中的聚类中心集合,那么每个数据点 xxx将根据以下公式被分配到一个聚类中:
argminci∈C dist(ci,x)2\underset{c_i \in C}{\arg\min} \; dist(c_i,x)^2ci∈Cargmindist(ci,x)2
其中, dist( · ) 是标准的(L2L_2L2)欧几里得距离。设每个第 (i)(i)(i) 个聚类中心的数据点分配集合为 SiS_iSi。
聚类中心更新步骤:在这个步骤中,聚类中心会被重新计算。这是通过取分配给该聚类中心的所有数据点的均值来完成的:
ci=1∣Si∣∑xi∈Sixic_i=\frac{1}{|S_i|}\sum_{x_i \in S_i x_i}ci=∣Si∣1xi∈Sixi∑
算法会在步骤一和步骤二之间迭代,直到满足停止条件(例如,没有数据点改变聚类,距离之和最小化,或者达到某个最大迭代次数)。
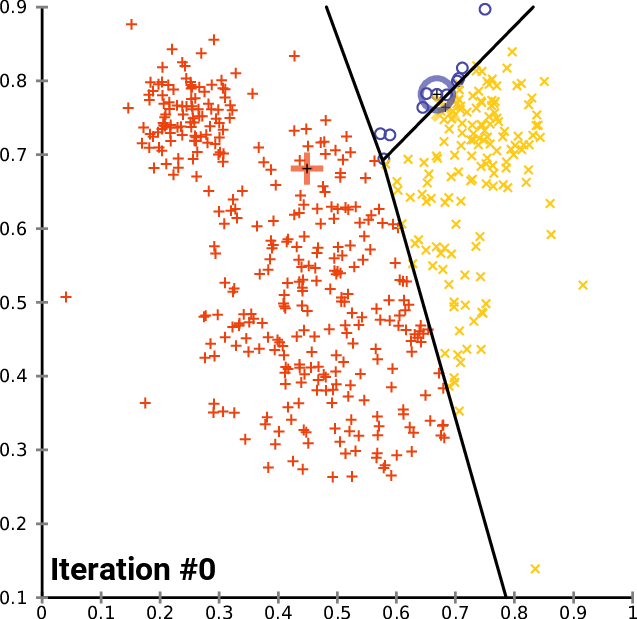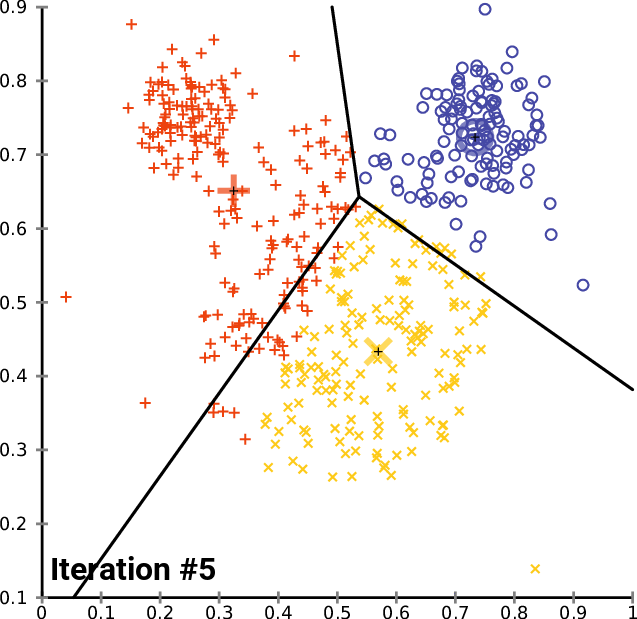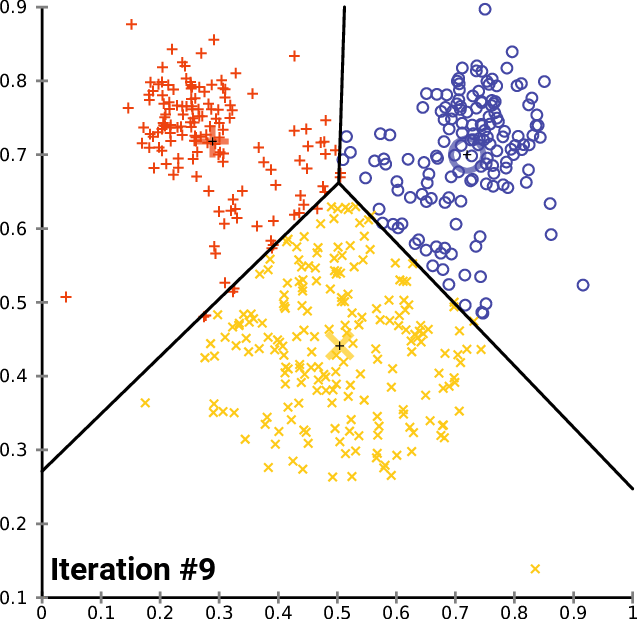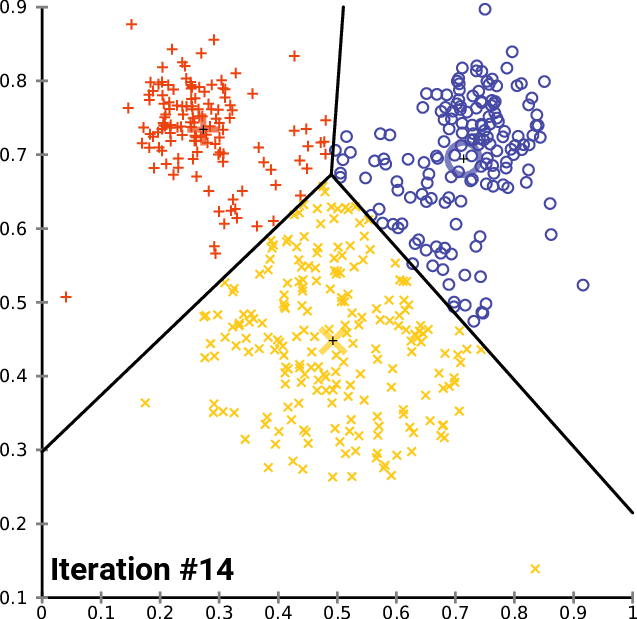
收敛性和随机初始化
该算法保证会收敛到一个结果。然而,这个结果可能是一个局部最优解(即不一定是最佳可能的结果),这意味着多次运行算法并随机选择初始聚类中心,可能会得到更好的结果。
优点
- 原理简单,容易理解和实现。
- 计算复杂度较低,在处理大规模数据时具有较高的效率。
- 对于处理具有球形分布的数据聚类效果较好。
缺点
- 需要事先指定聚类的数目 K,而 K 的选择往往具有一定的主观性,不同的 K 值可能会导致不同的聚类结果。
- 对初始聚类中心的选择较为敏感,不同的初始值可能会使算法收敛到不同的局部最优解。
- 对于非球形分布的数据或存在噪声的数据,聚类效果可能不理想。
1.2 实验前准备
对于这个实验,我们将尝试使用KMeans聚类将大学分为两组,私立和公立。我们将使用一个对以下18个变量进行777次观测的数据帧。
- Private A factor with levels No and Yes indicating private or public university
- Apps Number of applications received
- Accept Number of applications accepted
- Enroll Number of new students enrolled
- Top10perc Pct. new students from top 10% of H.S. class
- Top25perc Pct. new students from top 25% of H.S. class
- F.Undergrad Number of fulltime undergraduates
- P.Undergrad Number of parttime undergraduates
- Outstate Out-of-state tuition
- Room.Board Room and board costs
- Books Estimated book costs
- Personal Estimated personal spending
- PhD Pct. of faculty with Ph.D.’s
- Terminal Pct. of faculty with terminal degree
- S.F.Ratio Student/faculty ratio
- perc.alumni Pct. alumni who donate
- Expend Instructional expenditure per student
- Grad.Rate Graduation rate
获取数据
!wget --no-check-certificate https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_datasets/2693abae16b111f0a998fa163edcddae/College_Data.zip
!unzip College_Data.zip
环境准备
%pip install seaborn ipywidgets
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
使用read_csv读取College_Data文件。弄清楚如何将第一列设置为索引。
df = pd.read_csv('College_Data',index_col=0)
检查数据的头部
df.head()
检查数据上的info()和describee()方法。
df.info()
df.describe()
1.3 探索性分析
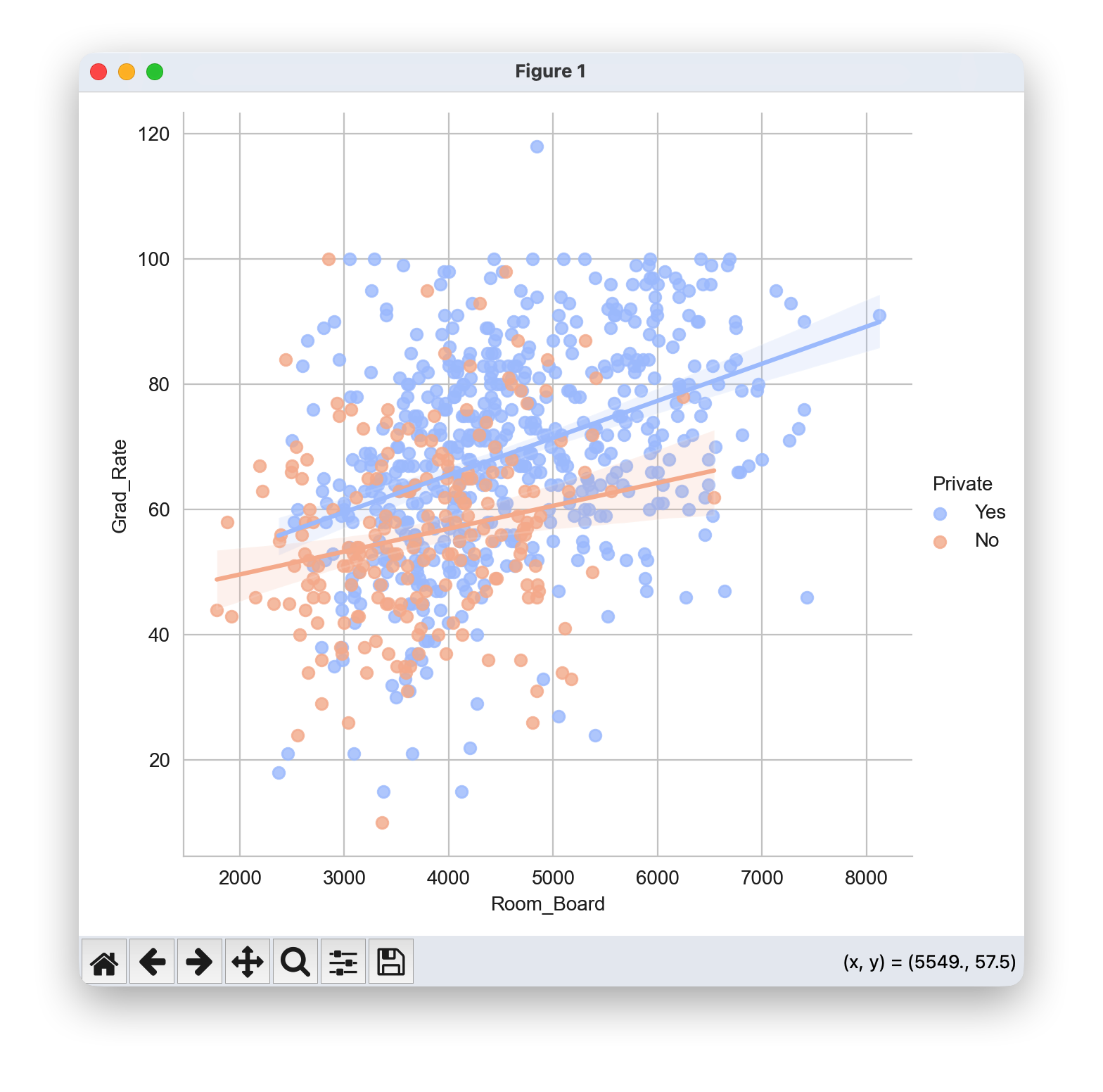
创建Grad散点图。价格与房间。板(及其线性拟合),其中点由Private列着色
# 设置绘图样式
sns.set_style('whitegrid')
# 正确调用方式
sns.lmplot(x='Room_Board', y='Grad_Rate', data=df, hue='Private', palette='coolwarm', height=6, aspect=1, fit_reg=True)
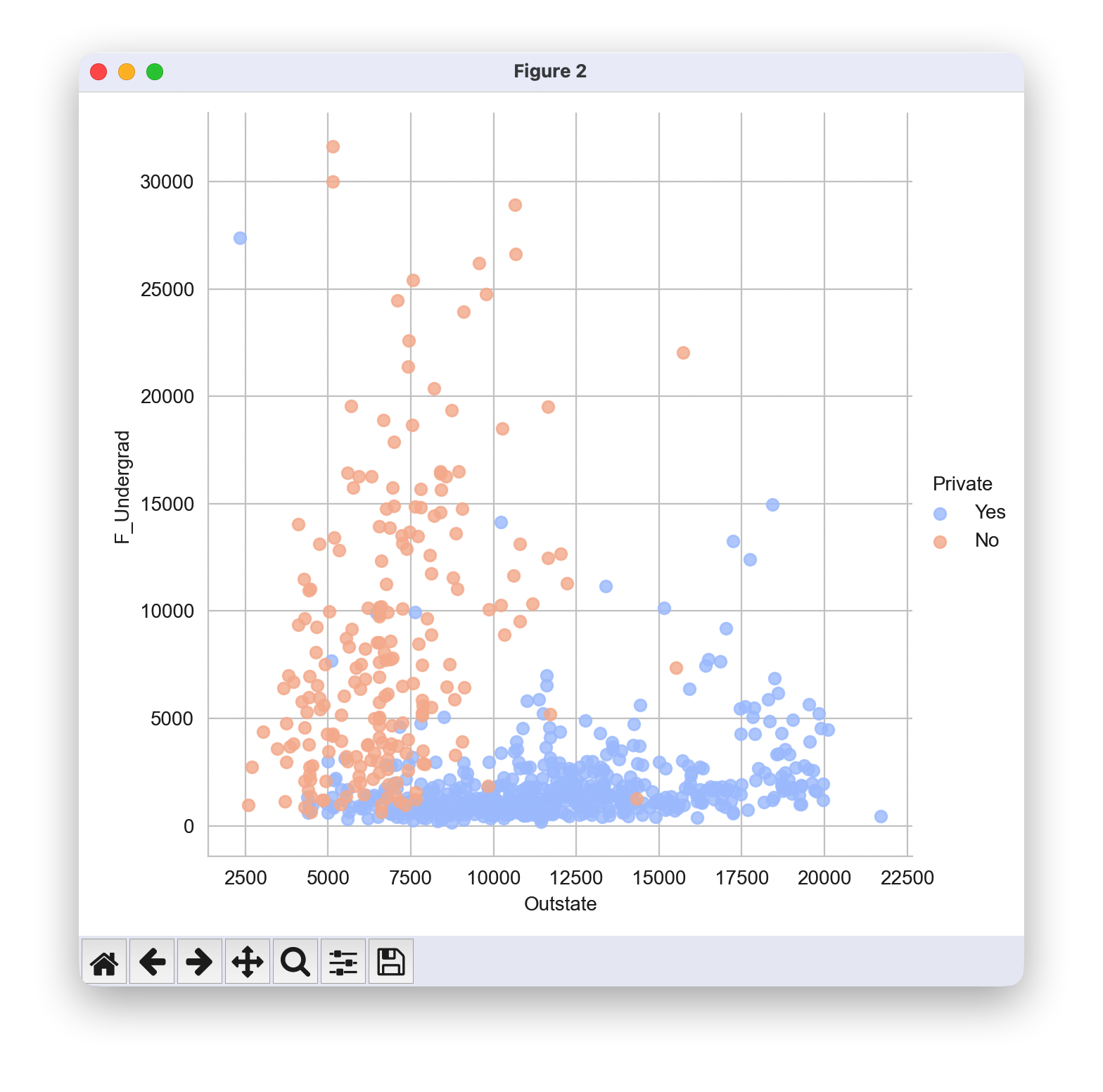
创建一个以 F.Undergrad 为横轴、Outstate 为纵轴的散点图,其中的点根据 Private 列进行着色。
该图表表明,这两个特征维度可以根据学院的类型进行区分。
# 设置绘图样式
sns.set_style('whitegrid')
# 绘制线性回归图,不拟合回归直线
sns.lmplot(x='Outstate', y='F_Undergrad', data=df, hue='Private',
palette='coolwarm', height=6, aspect=1, fit_reg=False)
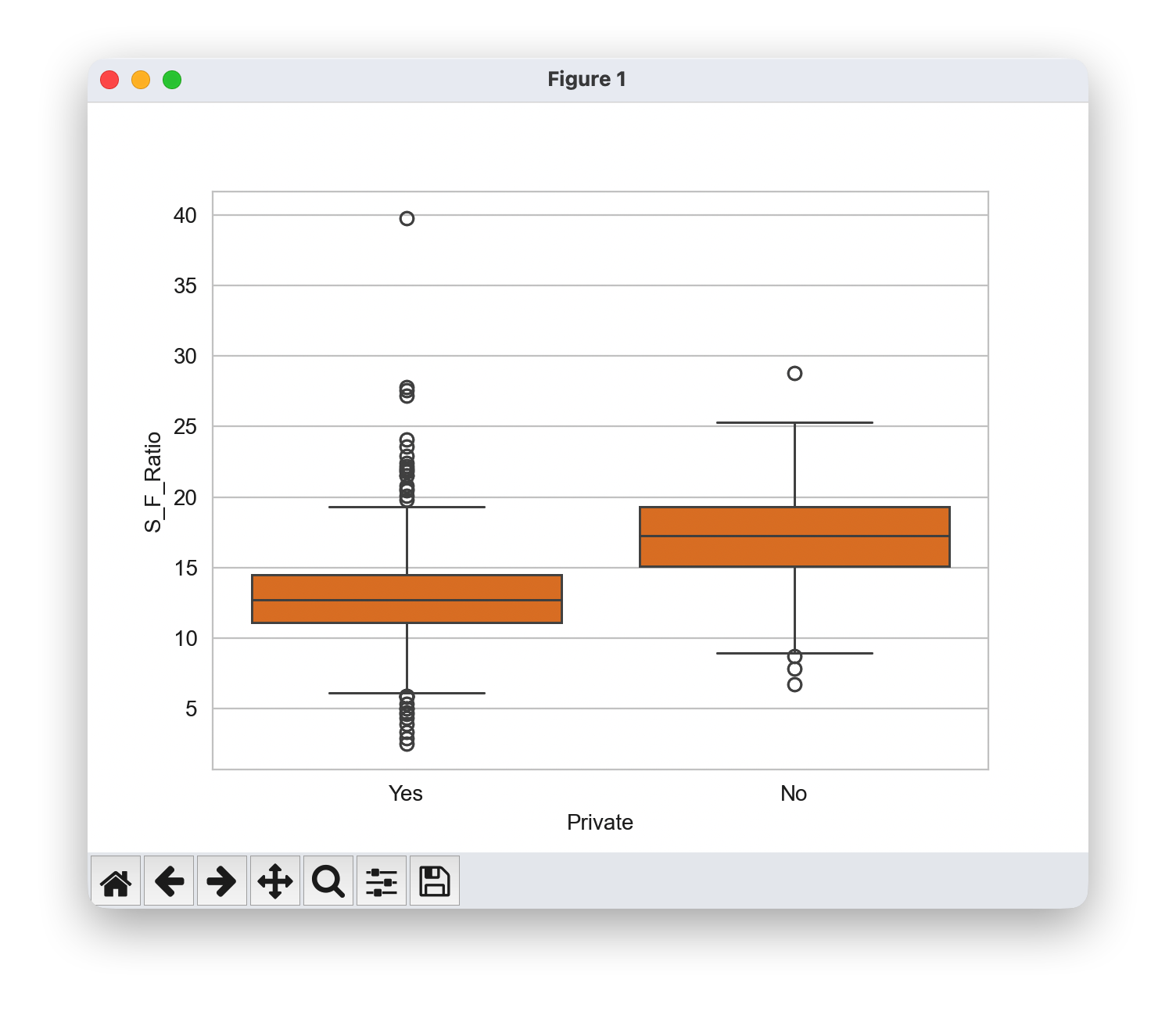
根据学院类型绘制学生与教师比例的箱线图
sns.boxplot(x='Private',y='S_F_Ratio',data=df)
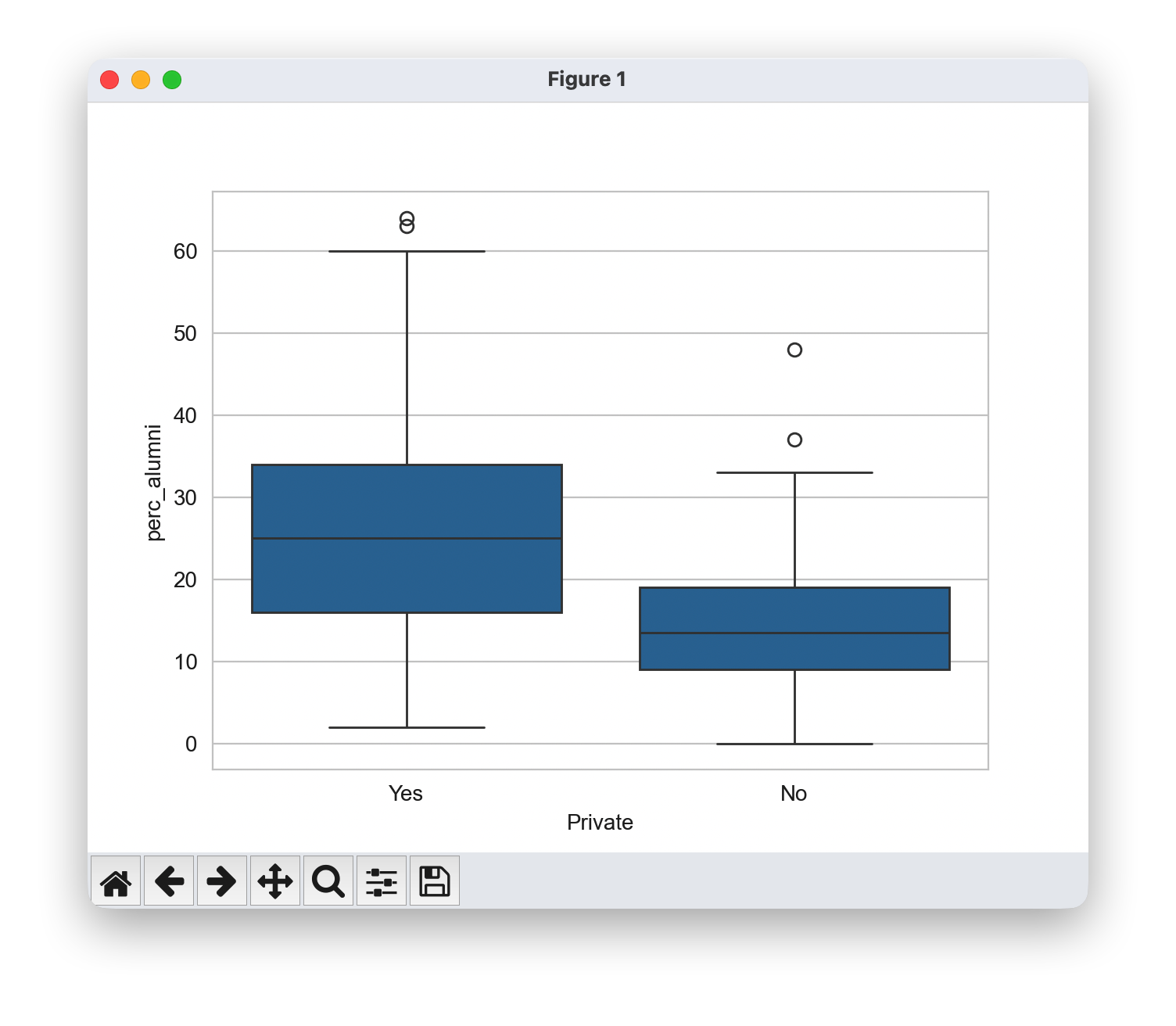
根据学院类型绘制校友捐赠比例的箱线图。
sns.boxplot(x='Private',y='perc_alumni',data=df)
根据“Private”列绘制“州外学费”(Out of State Tuition)的堆叠直方图。
# 设置绘图样式
sns.set_style('darkgrid')
#创建分面网格,使用 height 代替 size
g = sns.FacetGrid(df, hue="Private", palette='coolwarm', height=6, aspect=2)
# 在分面网格上绘制直方图
g = g.map(plt.hist,'Outstate',bins=20,alpha=0.7)
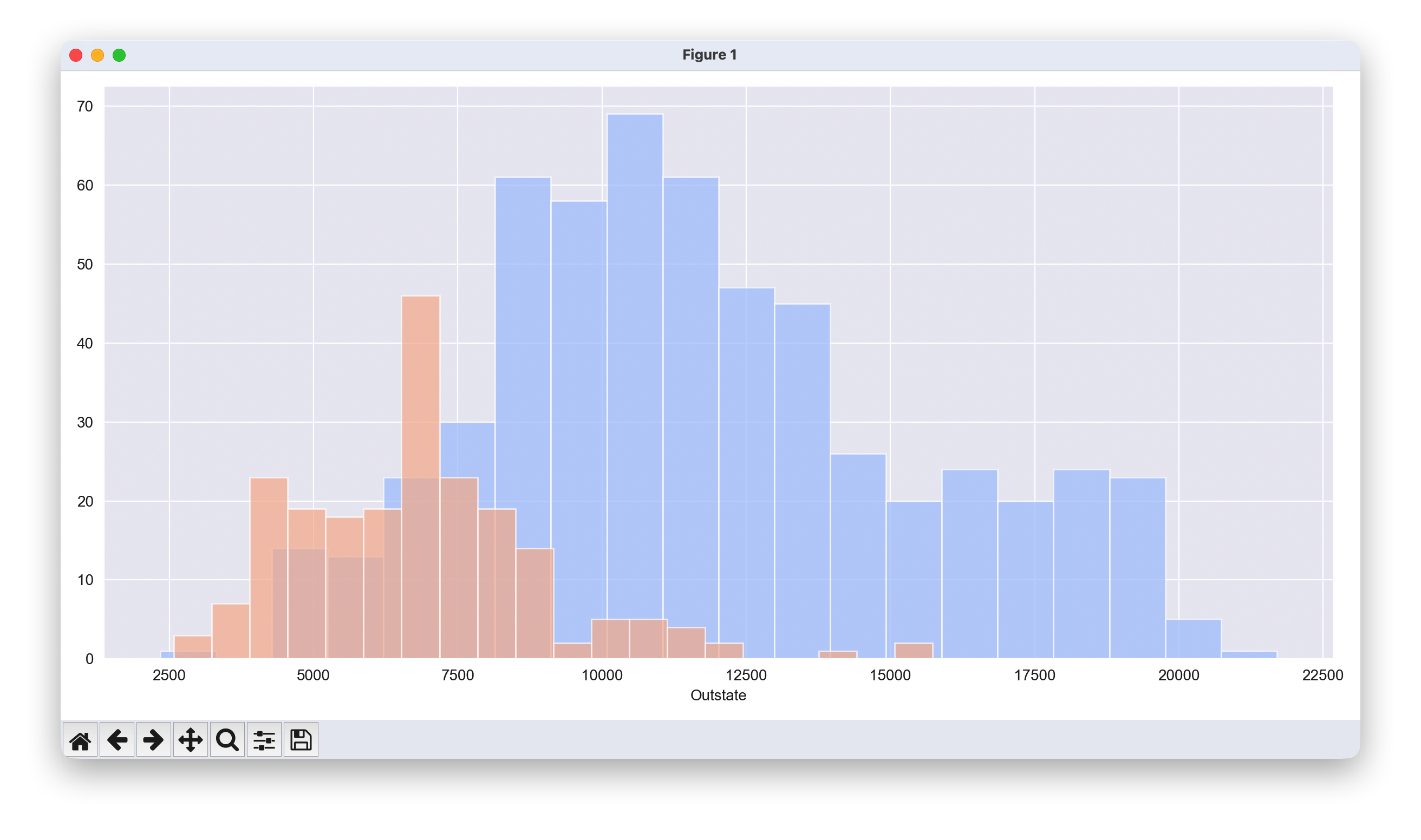
为 Grad.Rate 列创建一个类似的直方图。
# 设置绘图样式
sns.set_style('darkgrid')
# 创建分面网格
g = sns.FacetGrid(df, hue="Private", palette='coolwarm', height=6, aspect=2)
# 在分面网格上绘制直方图
g = g.map(plt.hist,'Grad_Rate',bins=20,alpha=0.7)
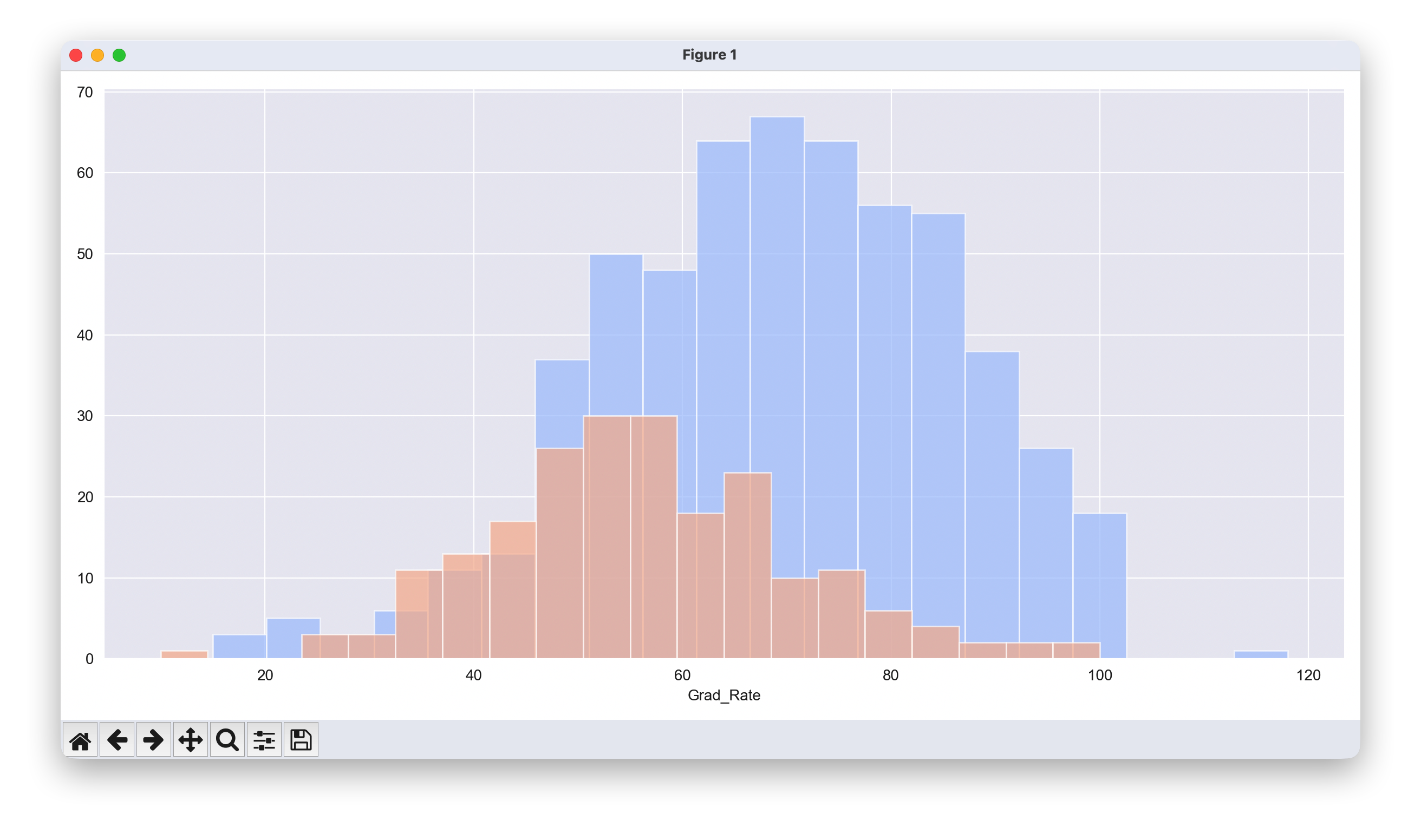
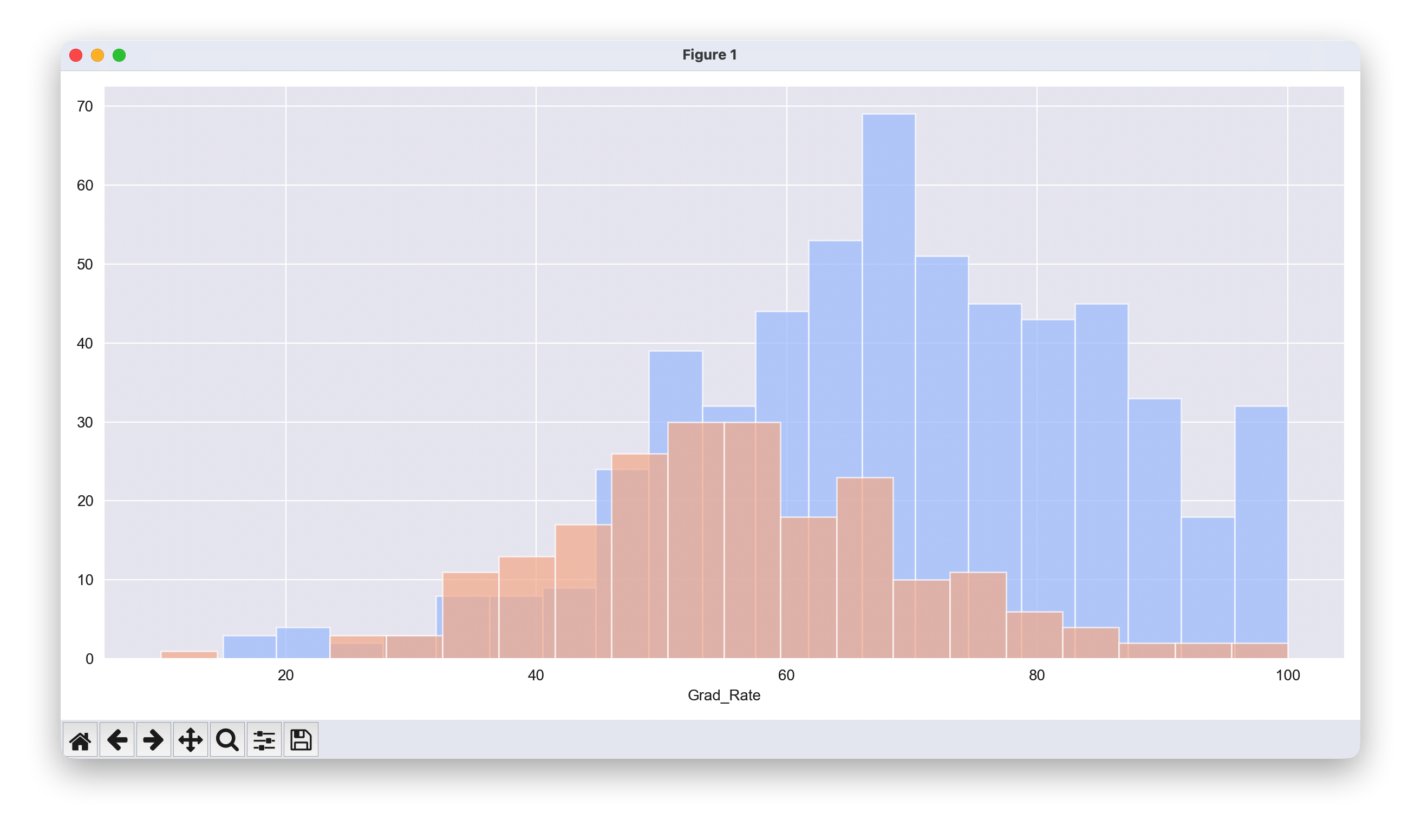
有一所私立学校的毕业率超过了100%。
df[df['Grad_Rate'] > 100]
df.loc["Grad_Rate", "Cazenovia College"]=100
# 设置绘图样式
sns.set_style('darkgrid')
# 创建分面网格,使用 height 替代 size
g = sns.FacetGrid(df, hue="Private", palette='coolwarm', height=6, aspect=2)
# 在分面网格上绘制直方图
g = g.map(plt.hist,'Grad_Rate',bins=20,alpha=0.7)
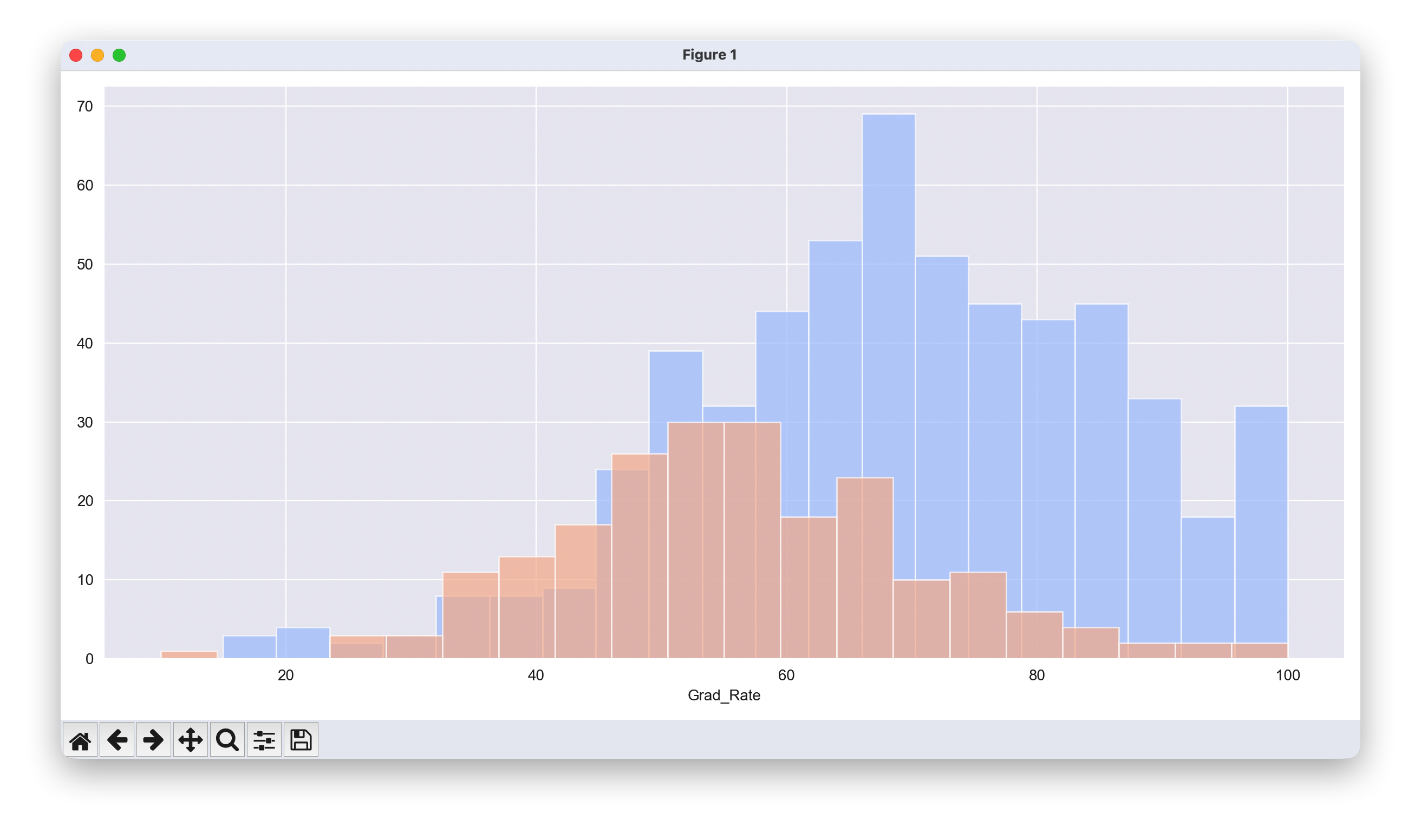
特征标准化的重要性分析
K-Means算法基于欧几里得距离进行聚类,这使得特征的尺度差异对算法结果产生决定性影响。当不同特征具有不同的数值范围时,数值较大的特征会在距离计算中占主导地位,从而扭曲聚类结果。
让我们首先分析当前数据集中各特征的尺度差异:
1.4 K-Means聚类的创建
从 SciKit Learn 中导入 KMeans。
from sklearn.cluster import KMeans
创建一个包含2个聚类的K均值模型实例。
kmeans = KMeans(n_clusters=2,verbose=0,tol=1e-3,max_iter=300,n_init=20)
将模型拟合到除“Private”标签之外的所有数据上。
kmeans.fit(df.drop('Private',axis=1))
聚类中心向量是什么?
clus_cent=kmeans.cluster_centers_
clus_cent
现在将这些聚类中心(针对所有维度/特征)与已知标记数据的平均值进行比较。
df[df['Private']=='Yes'].describe()
df[df['Private']=='No'].describe()
创建一个包含聚类中心的数据框,并从原始数据框中借用列名。
df_desc=pd.DataFrame(df.describe())
feat = list(df_desc.columns)
kmclus = pd.DataFrame(clus_cent,columns=feat)
kmclus
聚类标签
kmeans.labels_
K-Means算法工作原理的交互式可视化
K-Means算法的核心思想在于其迭代优化过程,但这个动态过程很难通过静态图表完全理解。算法的收敛路径、初始化的影响以及不同参数设置的效果,都需要通过动态交互来深入体会。
下面我们将创建交互式工具,让你能够实时观察K-Means算法的工作机制,理解其几何直觉和收敛特性。
try:
from ipywidgets import interact, IntSlider, FloatSlider, Dropdown, Checkbox, Button
import ipywidgets as widgets
print("交互式组件已准备就绪")
except ImportError:
print("请安装ipywidgets")
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
import numpy as np
# 准备用于可视化的2D数据
def prepare_2d_data():
"""选择最能区分公私立学校的两个特征进行2D可视化"""
# 使用标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(df.drop('Private', axis=1))
df_scaled = pd.DataFrame(X_scaled, columns=df.drop('Private', axis=1).columns, index=df.index)
# 选择区分度最高的两个特征
feature_x, feature_y = 'Outstate', 'F_Undergrad' # 基于之前EDA的观察
X_2d = df_scaled[[feature_x, feature_y]].values
labels_true = (df['Private'] == 'Yes').astype(int)
return X_2d, labels_true, feature_x, feature_y
X_2d, labels_true, feature_x, feature_y = prepare_2d_data()
def interactive_kmeans_visualization(k=2, init_method='random', max_iter=10, show_steps=False,
random_seed=42, show_true_labels=True):
"""
交互式K-Means可视化工具
参数:
- k: 聚类数量
- init_method: 初始化方法
- max_iter: 最大迭代次数
- show_steps: 是否显示迭代步骤
- random_seed: 随机种子
- show_true_labels: 是否显示真实标签
"""
# 设置随机种子确保可重现性
np.random.seed(random_seed)
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# 左图:真实标签分布(如果选择显示)
if show_true_labels:
colors_true = ['red', 'blue']
for i in range(2):
mask = labels_true == i
axes[0].scatter(X_2d[mask, 0], X_2d[mask, 1],
c=colors_true[i], alpha=0.6, s=50,
label=f"{'Private' if i==1 else 'Public'}")
axes[0].set_title('True Label Distribution\n(Public vs Private)', fontsize=12)
axes[0].set_xlabel(f'{feature_x} (Standardized)')
axes[0].set_ylabel(f'{feature_y} (Standardized)')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
else:
axes[0].scatter(X_2d[:, 0], X_2d[:, 1], c='gray', alpha=0.6, s=50)
axes[0].set_title('Raw Data Points\n(No Label Information)', fontsize=12)
axes[0].set_xlabel(f'{feature_x} (Standardized)')
axes[0].set_ylabel(f'{feature_y} (Standardized)')
axes[0].grid(True, alpha=0.3)
# 中图:K-Means聚类过程
if init_method == 'random':
init_centers = np.random.uniform(low=X_2d.min(axis=0), high=X_2d.max(axis=0), size=(k, 2))
elif init_method == 'k-means++':
kmeans_temp = KMeans(n_clusters=k, init='k-means++', n_init=1, random_state=random_seed)
kmeans_temp.fit(X_2d)
init_centers = kmeans_temp.cluster_centers_
else: # manual
# 手动设置一些初始中心点
init_centers = np.array([[-1, -1], [1, 1]])[:k]
# 执行K-Means算法
kmeans = KMeans(n_clusters=k, init=init_centers, n_init=1, max_iter=max_iter, random_state=random_seed)
labels_pred = kmeans.fit_predict(X_2d)
# 绘制聚类结果
colors_kmeans = ['red', 'blue', 'green', 'purple', 'orange'][:k]
for i in range(k):
mask = labels_pred == i
axes[1].scatter(X_2d[mask, 0], X_2d[mask, 1],
c=colors_kmeans[i], alpha=0.6, s=50,
label=f'Cluster {i}')
# 绘制最终聚类中心
axes[1].scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
c='black', marker='x', s=200, linewidths=3, label='Final Centers')
# 如果显示步骤,绘制初始中心
if show_steps:
axes[1].scatter(init_centers[:, 0], init_centers[:, 1],
c='red', marker='s', s=100, alpha=0.7, label='Initial Centers')
axes[1].set_title(f'K-Means Clustering Result\nK={k}, Iterations: {kmeans.n_iter_}', fontsize=12)
axes[1].set_xlabel(f'{feature_x} (Standardized)')
axes[1].set_ylabel(f'{feature_y} (Standardized)')
axes[1].legend()
axes[1].grid(True, alpha=0.3)
# 右图:性能指标对比
from sklearn.metrics import adjusted_rand_score, silhouette_score
# 计算各种评估指标
if show_true_labels:
ari = adjusted_rand_score(labels_true, labels_pred)
else:
ari = 0
if len(set(labels_pred)) > 1: # 确保至少有2个聚类
silhouette = silhouette_score(X_2d, labels_pred)
inertia = kmeans.inertia_
else:
silhouette = 0
inertia = 0
# 计算聚类内平均距离和聚类间距离
centers = kmeans.cluster_centers_
if len(centers) >= 2:
from scipy.spatial.distance import pdist
inter_cluster_dist = np.mean(pdist(centers))
else:
inter_cluster_dist = 0
metrics = ['Adjusted Rand\nIndex', 'Silhouette\nScore', 'Within-cluster\nSum of Squares\n(×1000)', 'Inter-cluster\nDistance']
values = [ari, silhouette, inertia/1000, inter_cluster_dist]
colors_metrics = ['lightblue', 'lightgreen', 'lightcoral', 'lightyellow']
bars = axes[2].bar(range(len(metrics)), values, color=colors_metrics, alpha=0.7)
axes[2].set_title('Clustering Performance Metrics', fontsize=12)
axes[2].set_xticks(range(len(metrics)))
axes[2].set_xticklabels(metrics, fontsize=9)
axes[2].set_ylabel('Metric Value')
axes[2].grid(axis='y', alpha=0.3)
# 添加数值标签
for bar, value in zip(bars, values):
height = bar.get_height()
axes[2].text(bar.get_x() + bar.get_width()/2., height + 0.01,
f'{value:.3f}', ha='center', va='bottom', fontsize=9)
plt.tight_layout()
plt.show()
# 输出详细分析结果
print("="*70)
print(f"K-Means聚类分析结果 (K={k})")
print("="*70)
print(f"算法收敛迭代次数: {kmeans.n_iter_}")
print(f"初始化方法: {init_method}")
if show_true_labels:
print(f"与真实标签一致性 (ARI): {ari:.3f}")
if ari > 0.5:
print(" - 聚类结果与真实标签高度一致")
elif ari > 0.2:
print(" - 聚类结果与真实标签中等一致")
else:
print(" - 聚类结果与真实标签一致性较低")
if silhouette > 0:
print(f"聚类质量 (轮廓系数): {silhouette:.3f}")
if silhouette > 0.5:
print(" - 聚类结构清晰,质量良好")
elif silhouette > 0.25:
print(" - 聚类结构中等,存在一定重叠")
else:
print(" - 聚类结构较弱,重叠较多")
print(f"类内平方和: {inertia:.0f}")
print(f"聚类中心间平均距离: {inter_cluster_dist:.3f}")
if k == 2:
print(f"\n关键观察:")
print(f"1. 该数据集在 {feature_x} 和 {feature_y} 两个维度上显示出一定的分离性")
print(f"2. K-Means试图在特征空间中找到最优的分割边界")
print(f"3. 不同初始化可能导致不同的局部最优解")
print("使用下面的交互控件探索K-Means算法的行为:")
print("-" * 60)
# 创建交互式可视化
interact(interactive_kmeans_visualization,
k=IntSlider(value=2, min=1, max=5, step=1,
description='聚类数量 K:', style={'description_width': 'initial'}),
init_method=Dropdown(options=['random', 'k-means++', 'manual'],
value='random', description='初始化方法:',
style={'description_width': 'initial'}),
max_iter=IntSlider(value=10, min=1, max=30, step=1,
description='最大迭代次数:', style={'description_width': 'initial'}),
show_steps=Checkbox(value=False, description='显示初始中心'),
random_seed=IntSlider(value=42, min=1, max=100, step=1,
description='随机种子:', style={'description_width': 'initial'}),
show_true_labels=Checkbox(value=True, description='显示真实标签'))
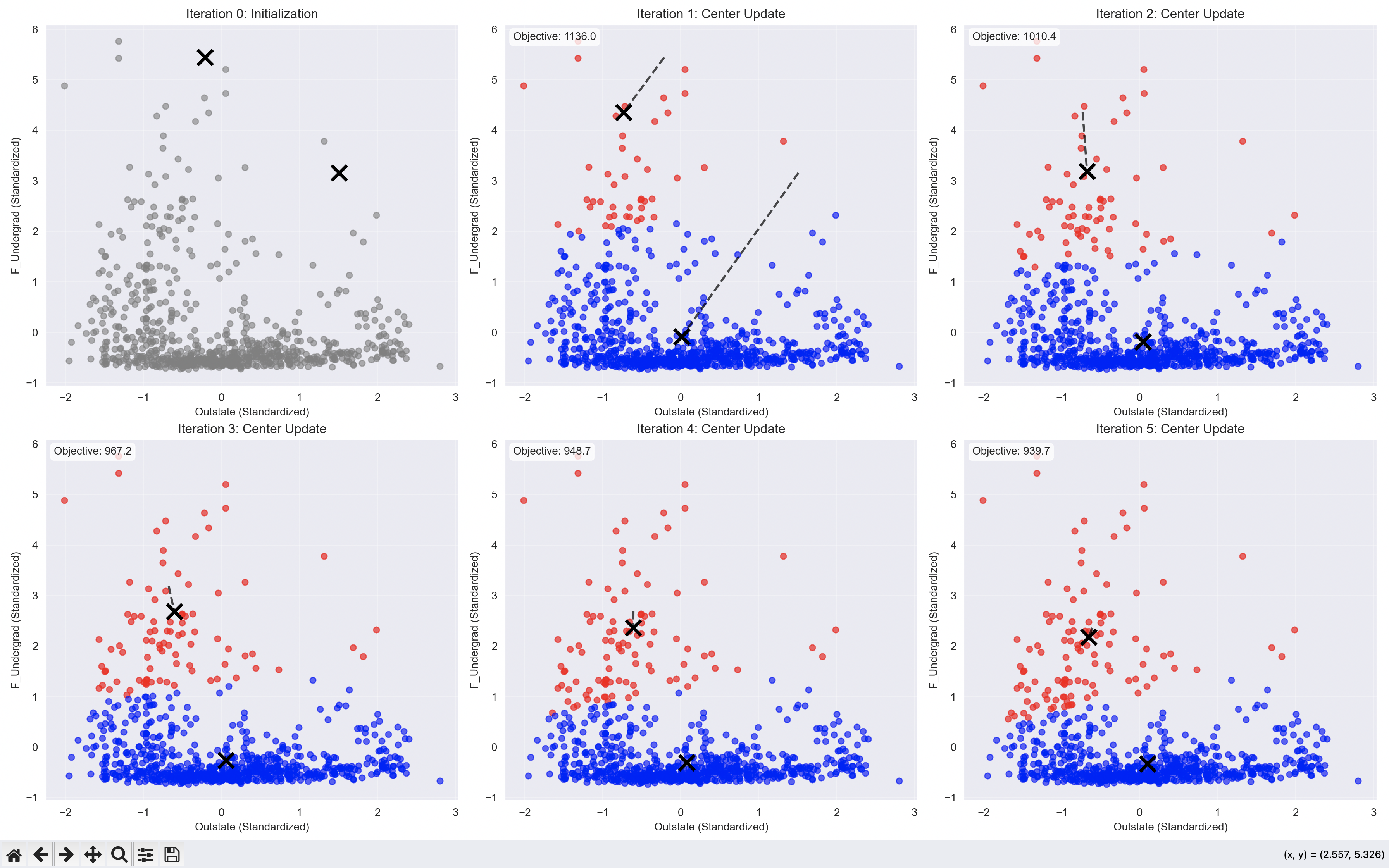
K-Means算法迭代过程动态展示
除了上述的交互式探索,我们还可以深入观察K-Means算法的逐步迭代过程,理解算法如何逐渐收敛到最优解:
def demonstrate_kmeans_convergence(n_clusters=2, random_state=42):
"""展示K-Means算法的逐步收敛过程"""
# 自定义K-Means实现以获取每一步的中心点
np.random.seed(random_state)
# 随机初始化聚类中心
centers = np.random.uniform(low=X_2d.min(axis=0), high=X_2d.max(axis=0),
size=(n_clusters, 2))
max_iters = 10
centers_history = [centers.copy()]
for iteration in range(max_iters):
# 分配步骤:计算每个点到各中心的距离,分配到最近的中心
distances = np.sqrt(((X_2d - centers[:, np.newaxis])**2).sum(axis=2))
labels = np.argmin(distances, axis=0)
# 更新步骤:计算新的聚类中心
new_centers = np.array([X_2d[labels == i].mean(axis=0) for i in range(n_clusters)])
# 检查收敛
if np.allclose(centers, new_centers, atol=1e-6):
print(f"算法在第 {iteration + 1} 次迭代后收敛")
break
centers = new_centers.copy()
centers_history.append(centers.copy())
# 可视化收敛过程
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
axes = axes.ravel()
colors = ['red', 'blue']
iterations_to_show = min(6, len(centers_history))
for i in range(iterations_to_show):
ax = axes[i]
current_centers = centers_history[i]
if i > 0:
# 计算当前迭代的标签
distances = np.sqrt(((X_2d - current_centers[:, np.newaxis])**2).sum(axis=2))
current_labels = np.argmin(distances, axis=0)
# 绘制数据点
for cluster_id in range(n_clusters):
mask = current_labels == cluster_id
ax.scatter(X_2d[mask, 0], X_2d[mask, 1],
c=colors[cluster_id], alpha=0.6, s=30)
else:
# 第一次迭代,所有点都是灰色
ax.scatter(X_2d[:, 0], X_2d[:, 1], c='gray', alpha=0.6, s=30)
# 绘制聚类中心
ax.scatter(current_centers[:, 0], current_centers[:, 1],
c='black', marker='x', s=200, linewidths=3)
# 如果不是第一次迭代,绘制中心点的移动轨迹
if i > 0:
for center_id in range(n_clusters):
ax.plot([centers_history[i-1][center_id, 0], current_centers[center_id, 0]],
[centers_history[i-1][center_id, 1], current_centers[center_id, 1]],
'k--', alpha=0.7, linewidth=2)
ax.set_title(f'Iteration {i}: {"Initialization" if i==0 else "Center Update"}', fontsize=12)
ax.set_xlabel(f'{feature_x} (Standardized)')
ax.set_ylabel(f'{feature_y} (Standardized)')
ax.grid(True, alpha=0.3)
# 计算并显示目标函数值(类内平方和)
if i > 0:
inertia = sum(np.sum((X_2d[current_labels == j] - current_centers[j])**2)
for j in range(n_clusters))
ax.text(0.02, 0.98, f'Objective: {inertia:.1f}',
transform=ax.transAxes, verticalalignment='top',
bbox=dict(boxstyle='round', facecolor='white', alpha=0.8))
# 隐藏多余的子图
for i in range(iterations_to_show, 6):
axes[i].set_visible(False)
plt.tight_layout()
plt.show()
print(f"\n收敛过程分析:")
print(f"- 算法共进行了 {len(centers_history)} 次迭代")
print(f"- 每次迭代包括两个步骤:数据分配 → 中心点更新")
print(f"- 聚类中心逐渐移动到各自聚类的重心位置")
print(f"- 目标函数(类内平方和)随迭代逐步减小")
demonstrate_kmeans_convergence()
print("\n实验建议:")
print("1. 尝试不同的K值,观察聚类边界的变化")
print("2. 改变随机种子,体验初始化对结果的影响")
print("3. 比较不同初始化方法的效果和收敛速度")
print("4. 观察轮廓系数等指标如何评估聚类质量")
1.5 评估
为df创建一个名为“Cluster”的新列,私立学校为1,公立学校为0。
def converter(cluster):
if cluster=='Yes':
return 1
else:
return 0
df1=df
df1['Cluster'] = df['Private'].apply(converter)
df1.head()
创建一个混淆矩阵和分类报告,以查看在没有给定任何标签的情况下,K均值聚类的效果如何。
from sklearn.metrics import confusion_matrix,classification_report
print(confusion_matrix(df1['Cluster'],kmeans.labels_))
print(classification_report(df1['Cluster'],kmeans.labels_))
1.6 聚类性能
创建两个数据框,一个只包含私立大学的数据,另一个只包含公立大学的数据。
修正数据,否则会报错:
# 检查是否有 nan 或 inf
print("是否存在缺失值:", np.isnan(X_2d).any())
print("是否存在无穷值:", np.isinf(X_2d).any())
# 清理异常值(示例:替换 inf 为有限值,删除含 nan 的行)
X_2d = np.where(np.isinf(X_2d), np.nan, X_2d) # 将 inf 转为 nan
X_2d = X_2d[~np.isnan(X_2d).any(axis=1)] # 删除含 nan 的行
# 检查清理后的数据范围
print("清理后的最小值:", X_2d.min(axis=0))
print("清理后的最大值:", X_2d.max(axis=0))
df_pvt=df[df['Private']=='Yes']
df_pub=df[df['Private']=='No']
调整参数,例如 max_iter 和 n_init,并计算聚类中心之间的距离。
kmeans = KMeans(n_clusters=2, verbose=0, tol=1e-3, max_iter=50, n_init=10)
kmeans.fit(df.drop('Private', axis=1))
clus_cent = kmeans.cluster_centers_
df_desc = pd.DataFrame(df.describe())
feat = list(df_desc.columns)
kmclus = pd.DataFrame(clus_cent, columns=feat)
a = np.array(kmclus.diff().iloc[1])
centroid_diff = pd.DataFrame(a, columns=['K-means cluster centroid-distance'], index=df_desc.columns)
# 计算均值时指定 numeric_only=True
centroid_diff['Mean of corresponding entity (private)'] = df_pvt.mean(numeric_only=True)
centroid_diff['Mean of corresponding entity (public)'] = df_pub.mean(numeric_only=True)
centroid_diff
修正




















 10万+
10万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








