K-Means 聚类与高斯混合模型
学习目标
通过本课程,你将了解到K-means和高斯混合模型的基本概念、从Scikit-learn中导入KMeans类并拟合数据、从零实现k-means算法、高斯混合模型绘制散点图、泛化到高斯混合模型等方法。
相关知识点
- K-Means聚类与高斯混合模型
学习内容
1 K-Means聚类与高斯混合模型
K-Means聚类和高斯混合模型(GMM)都是常用的聚类算法,但它们在原理和特性上有所不同。K-Means通过迭代将数据划分为K个簇,每个簇由一个质心表示,数据点被分配到最近的质心所对应的簇中,其目标是最小化簇内距离的平方和,计算简单且收敛速度快,但只能处理球形或近似球形的簇,且对初始质心的选择较为敏感。而高斯混合模型则假设数据是由多个高斯分布混合生成的,每个高斯分布对应一个簇,它通过估计每个分布的参数来确定数据点属于各个簇的概率,能够处理更复杂的簇形状,并且可以提供数据点属于每个簇的概率,但计算复杂度相对较高,需要使用期望最大化(EM)算法进行参数估计。
k-means 算法会在一个未标记的多维数据集中搜索预定义数量的聚类。它通过一个简单的最优聚类概念来实现这一目标:
- “聚类中心” 是属于该聚类的所有点的算术平均值。
- 每个点都比其他聚类中心更接近其自身的聚类中心。
1.1 实验前准备
%pip install seaborn
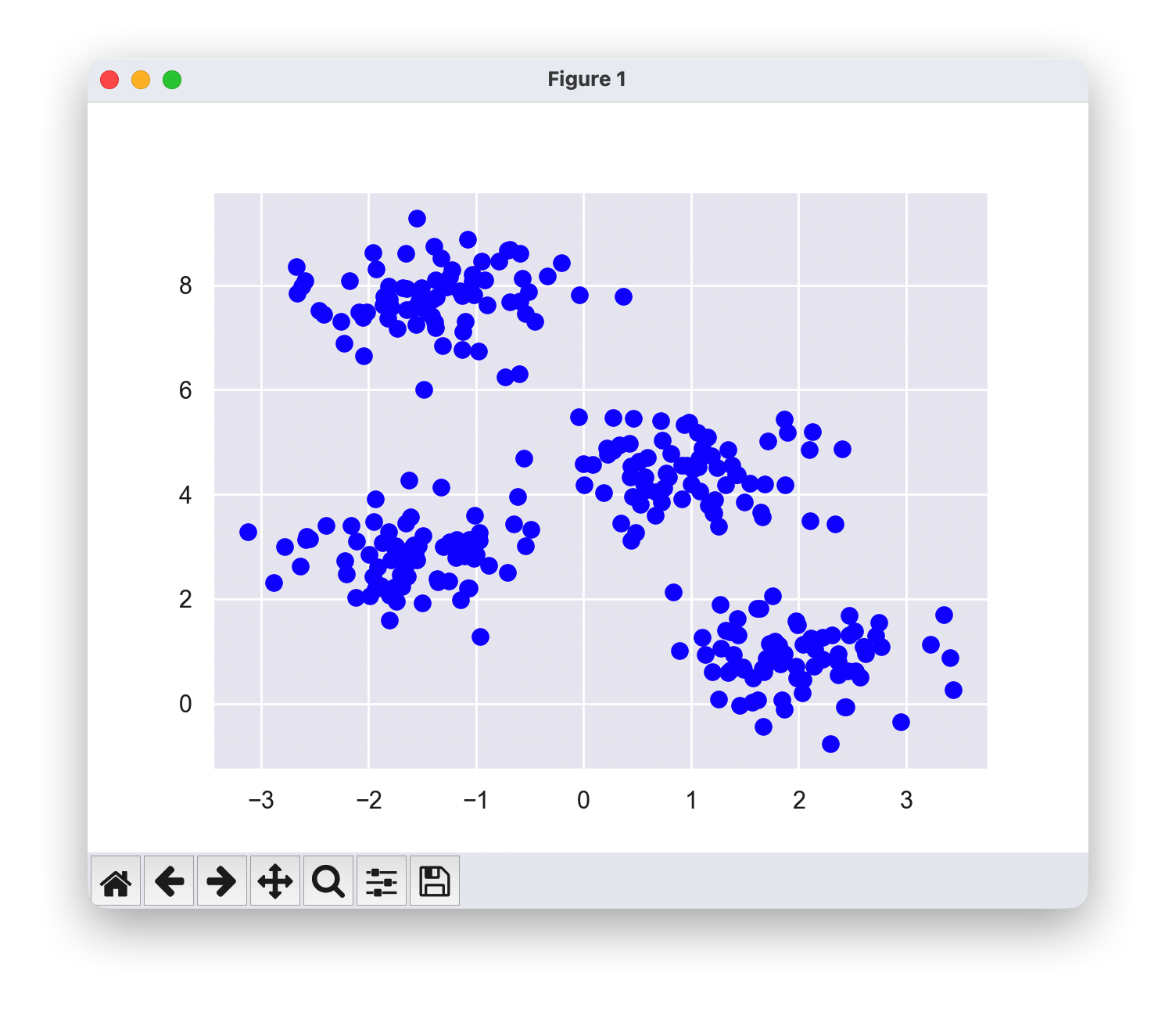
- 创建一个未标记的“blob”(团块)合成数据集。
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
import numpy as np
from sklearn.datasets import make_blobs
X, y_true = make_blobs(n_samples=300, centers=4,
cluster_std=0.60, random_state=0)
plt.scatter(X[:, 0], X[:, 1], s=50,color='blue');
1.2 从Scikit-learn中导入KMeans类并拟合数据
- 注意,这里我们没有进行测试集/训练集的划分,因为这是一种无监督机器学习技术。
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5);
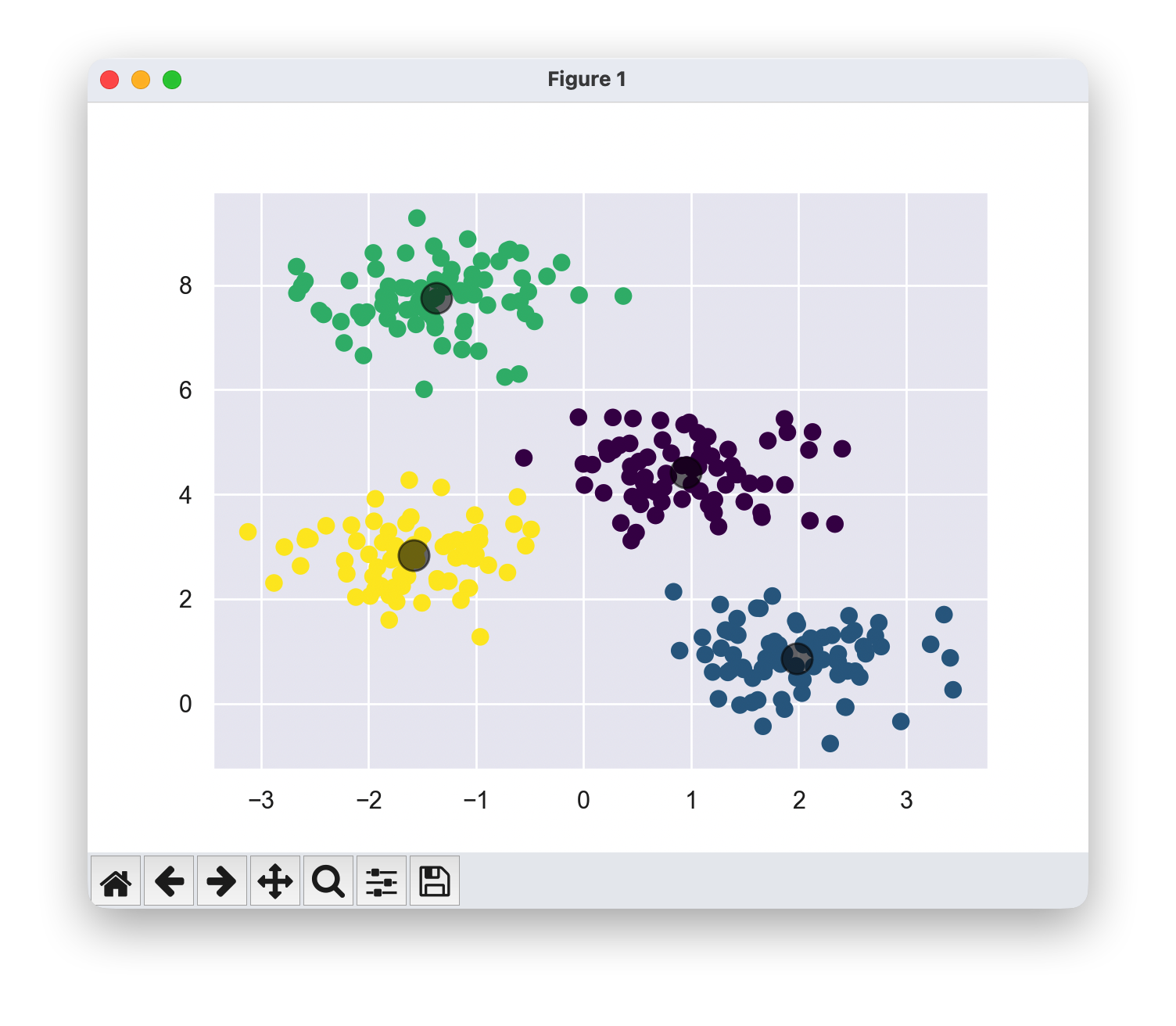
k-means是如何成为期望最大化(EM)算法的特例的
期望最大化(E-M)是一种强大的算法,在数据科学的许多领域都有应用。k-means是这种更通用算法的一个特别简单且特殊的案例。k-means的基本算法流程如下:
- 猜测一些聚类中心(初始化)
- 重复以下步骤,直到收敛:
- E-step:将点分配给最近的聚类中心
- M-Step:将聚类中心设置为均值
在这里,“E-step”或“Expectation step”涉及更新我们对每个点属于哪个聚类的期望。
“M-step”或“Maximization step”涉及最大化某个适应度函数,该函数定义了聚类中心的位置。在k-means的情况下,这种最大化是通过取每个聚类中数据的简单均值来实现的。
1.3 从零实现k-means算法
from sklearn.metrics import pairwise_distances_argmin
def find_clusters(X, n_clusters, rseed=2):
rng = np.random.RandomState(rseed)
i = rng.permutation(X.shape[0])[:n_clusters]
centers = X[i]
while True:
labels = pairwise_distances_argmin(X, centers)
new_centers = np.array([X[labels == i].mean(0)
for i in range(n_clusters)])
if np.all(centers == new_centers):
break
centers = new_centers
return centers, labels
centers, labels = find_clusters(X, 4)
plt.scatter(X[:, 0], X[:, 1], c=labels,s=50, cmap='viridis');
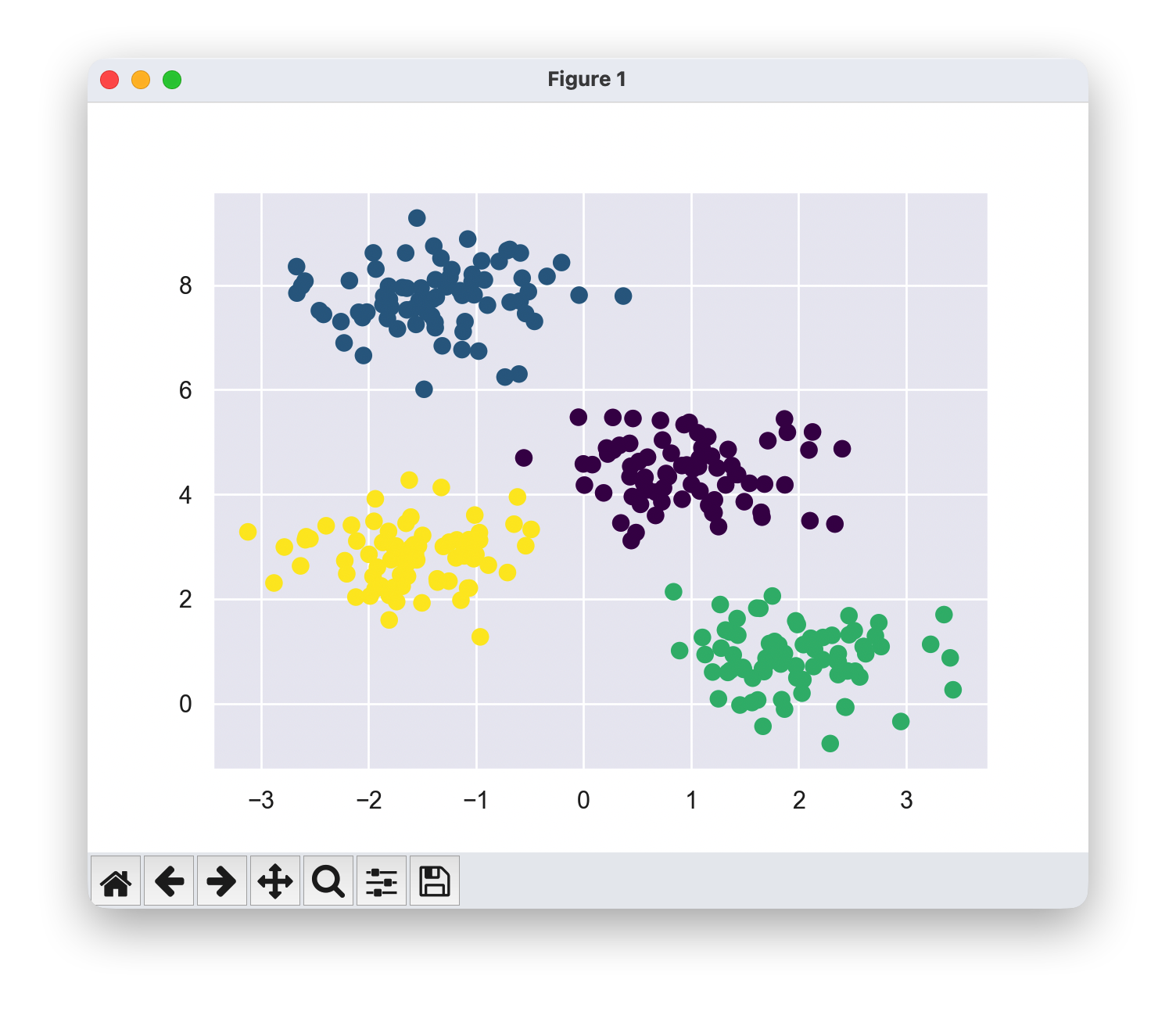
不保证最优性与初始化的重要性
在通常情况下,每次重复执行E步和M步都会使聚类特征的估计结果变得更好。然而,需要注意的是,尽管E-M过程保证在每一步都能改善结果,但无法确保它会导向全局最优解。
初始化至关重要,尤其是糟糕的初始化有时会导致明显次优的聚类结果。
centers, labels = find_clusters(X, 4, rseed=0)
plt.scatter(X[:, 0], X[:, 1], c=labels,
s=50, cmap='viridis');
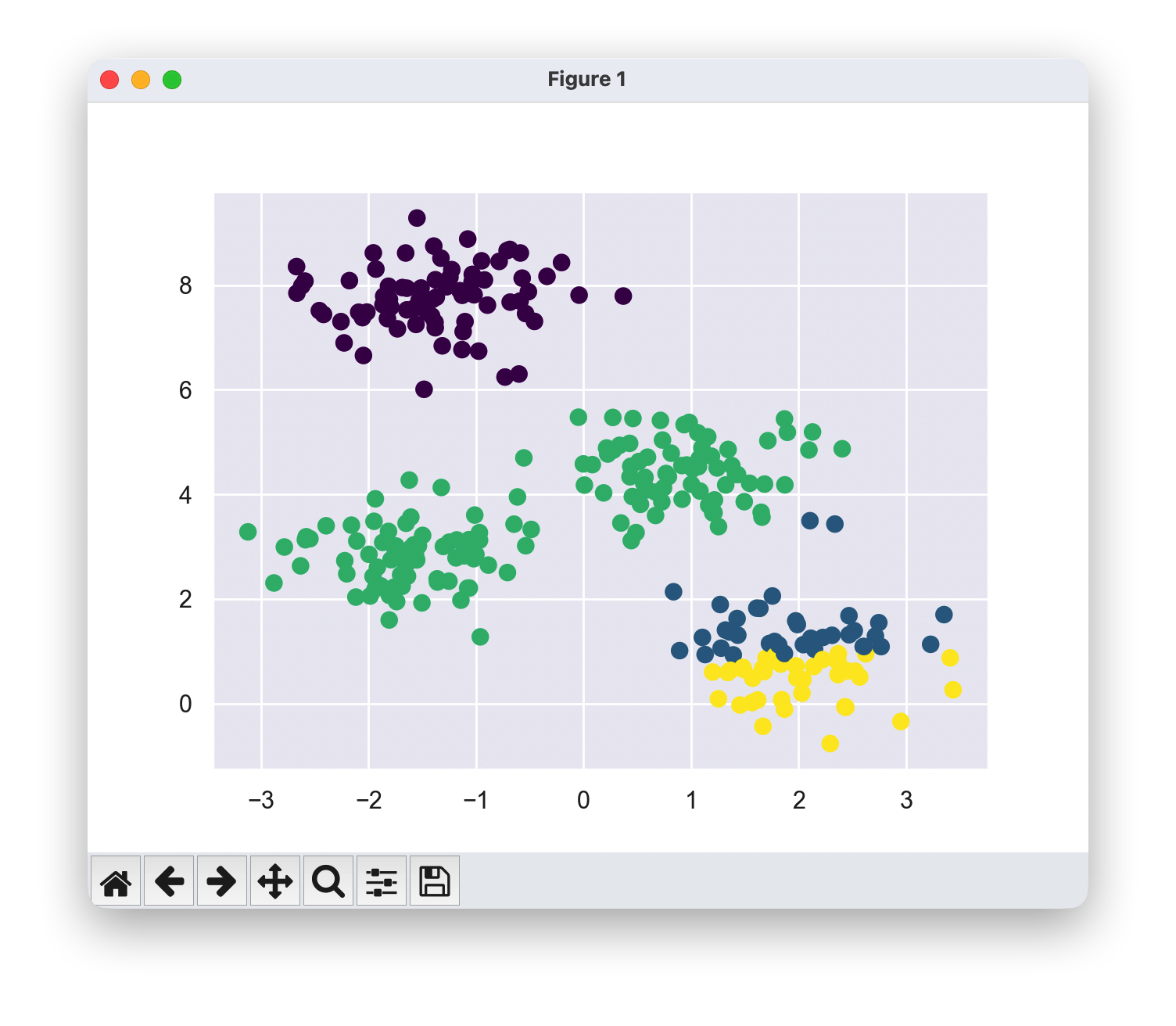
确定聚类数量
k-means的一个常见挑战是,你必须告诉它你期望的聚类数量。它无法从数据中自动学习聚类的数量。
如果我们强迫k-means寻找6个聚类,而不是4个,它会返回6个聚类,但这些聚类可能并不是我们想要的结果!
像**肘部法则(elbow)和轮廓分析(silhouette analysis)**这样的方法可以用来评估一个合适的聚类数量。
labels = KMeans(6, random_state=0).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels,
s=50, cmap='viridis');
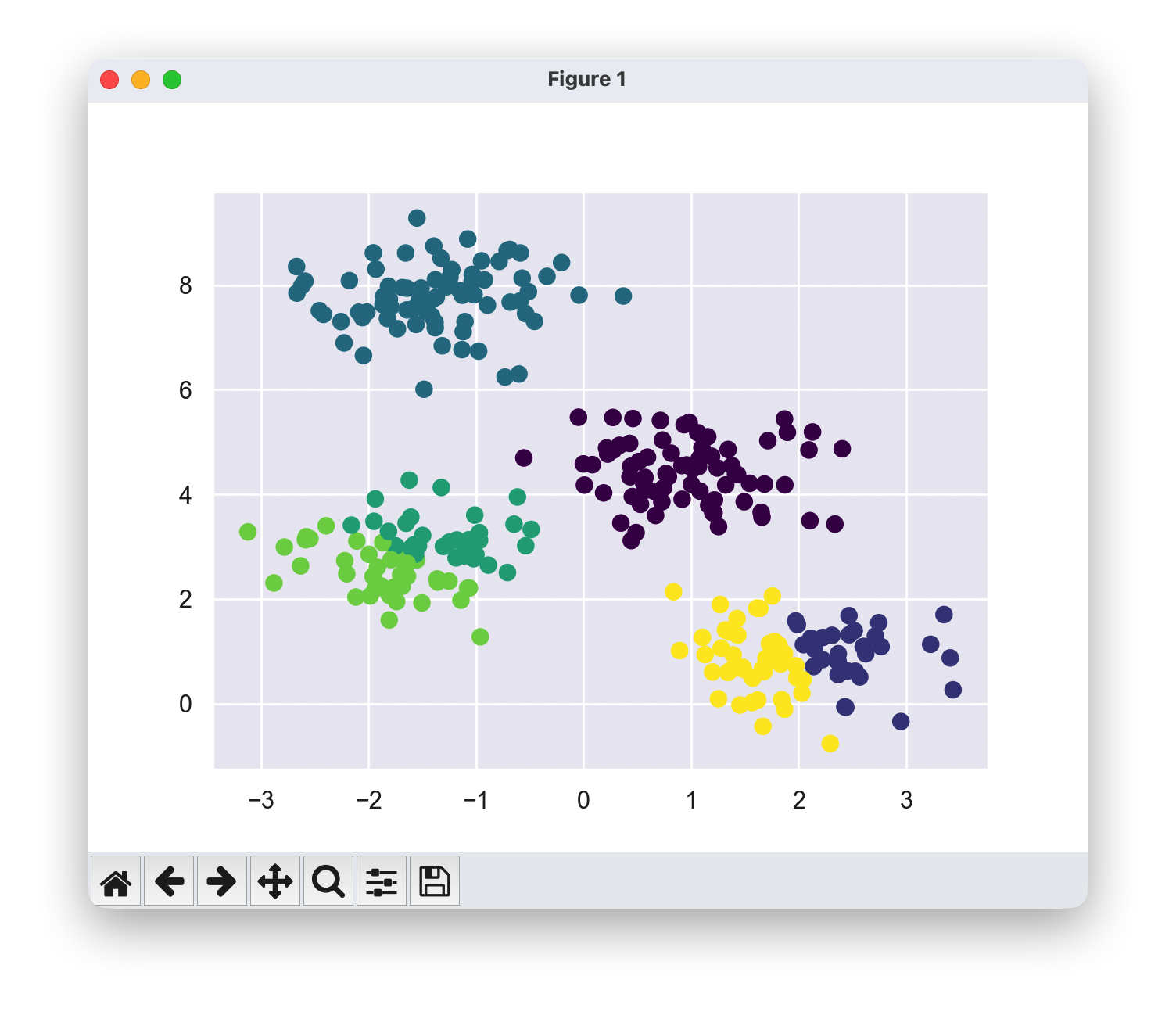
局限性-示例
如果聚类具有复杂的几何形状,k-means算法通常会效果不佳。特别是,k-means聚类之间的边界总是线性的,这意味着它对于更复杂的边界会失效
from sklearn.datasets import make_moons
X, y = make_moons(200, noise=.05, random_state=0)
labels = KMeans(2, random_state=0).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels,s=50, cmap='viridis');

核变换
上述情况让人联想到支持向量机(Support Vector Machines, SVM),在其中我们使用核变换将数据投影到更高维度,使得线性分离成为可能。我们可以想象使用相同的技巧,让k-means能够发现非线性边界。
Scikit-Learn中的SpectralClustering估计器实现了一种核化的k-means版本。它利用最近邻图来计算数据的高维表示,然后通过k-means算法分配标签。
from sklearn.cluster import SpectralClustering
model = SpectralClustering(n_clusters=2, affinity='nearest_neighbors',n_neighbors=30,
assign_labels='kmeans')
labels = model.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels,s=50, cmap='viridis');
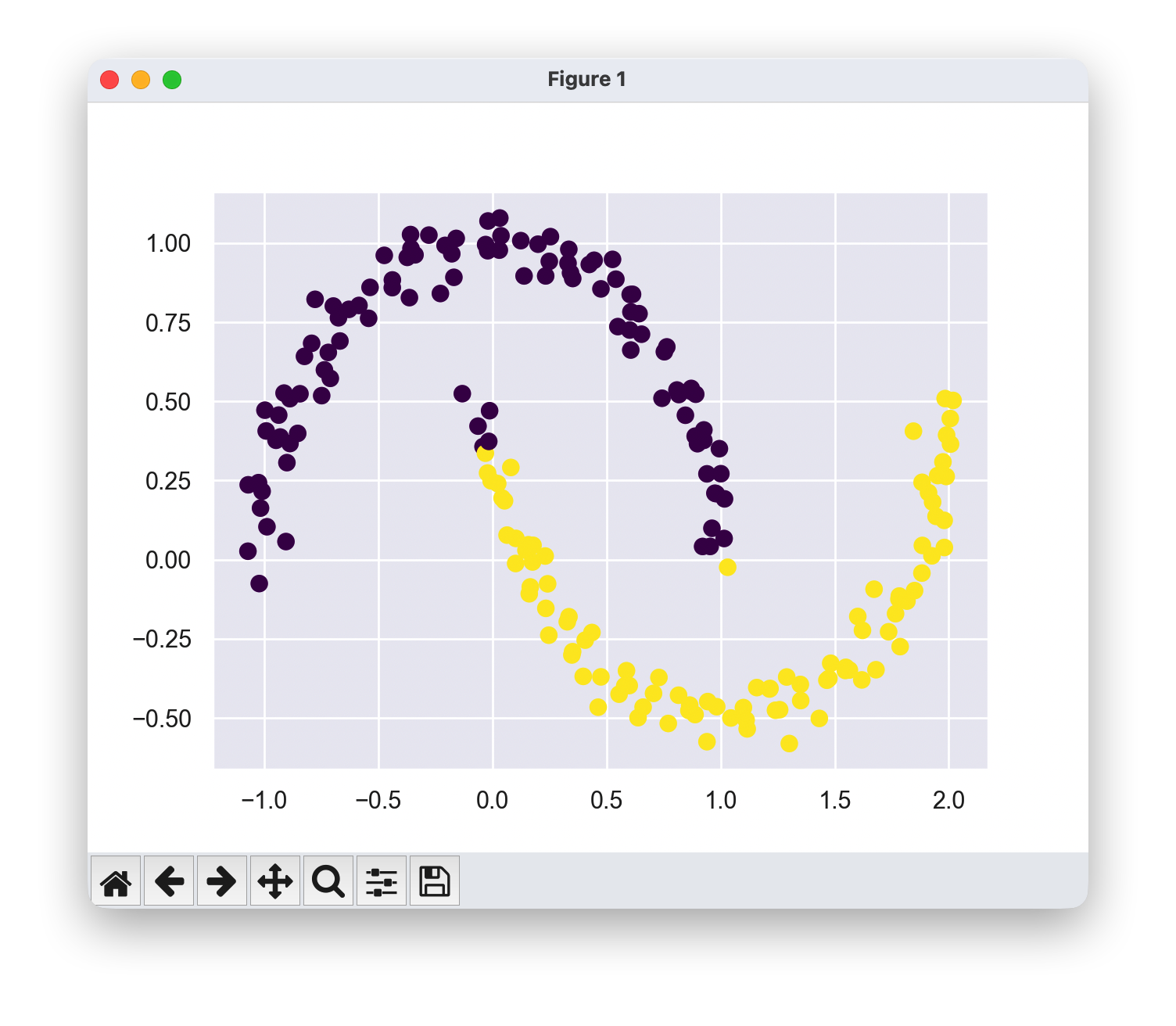
K-means的局限性
K-means的简单性是其快速处理大规模数据的一大优势,但这种简单性也导致了它在实际应用中面临诸多挑战。
特别是,K-means的非概率性本质以及其通过简单计算与聚类中心的距离来分配聚类成员资格的方式,使得它在许多现实情况下的表现不尽如人意。
高斯混合模型(GMMs)可以被视为K-means背后思想的扩展,但它们也可以作为一种强大的工具,用于超越简单聚类的估计。
from sklearn.datasets import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
cluster_std=0.7, random_state=0)
X = X[:, ::-1]
from sklearn.cluster import KMeans
kmeans = KMeans(4, random_state=0)
labels = kmeans.fit(X).predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis')
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
def plot_kmeans(kmeans, X, n_clusters=4, rseed=0, ax=None):
labels = kmeans.fit_predict(X)
ax = ax or plt.gca()
ax.axis('equal')
ax.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis', edgecolor='k',zorder=2)
centers = kmeans.cluster_centers_
radii = [cdist(X[labels == i], [center]).max()
for i, center in enumerate(centers)]
for c, r in zip(centers, radii):
ax.add_patch(plt.Circle(c, r, fc='#CCCCCC', lw=3, alpha=0.5, zorder=1))
kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans, X)
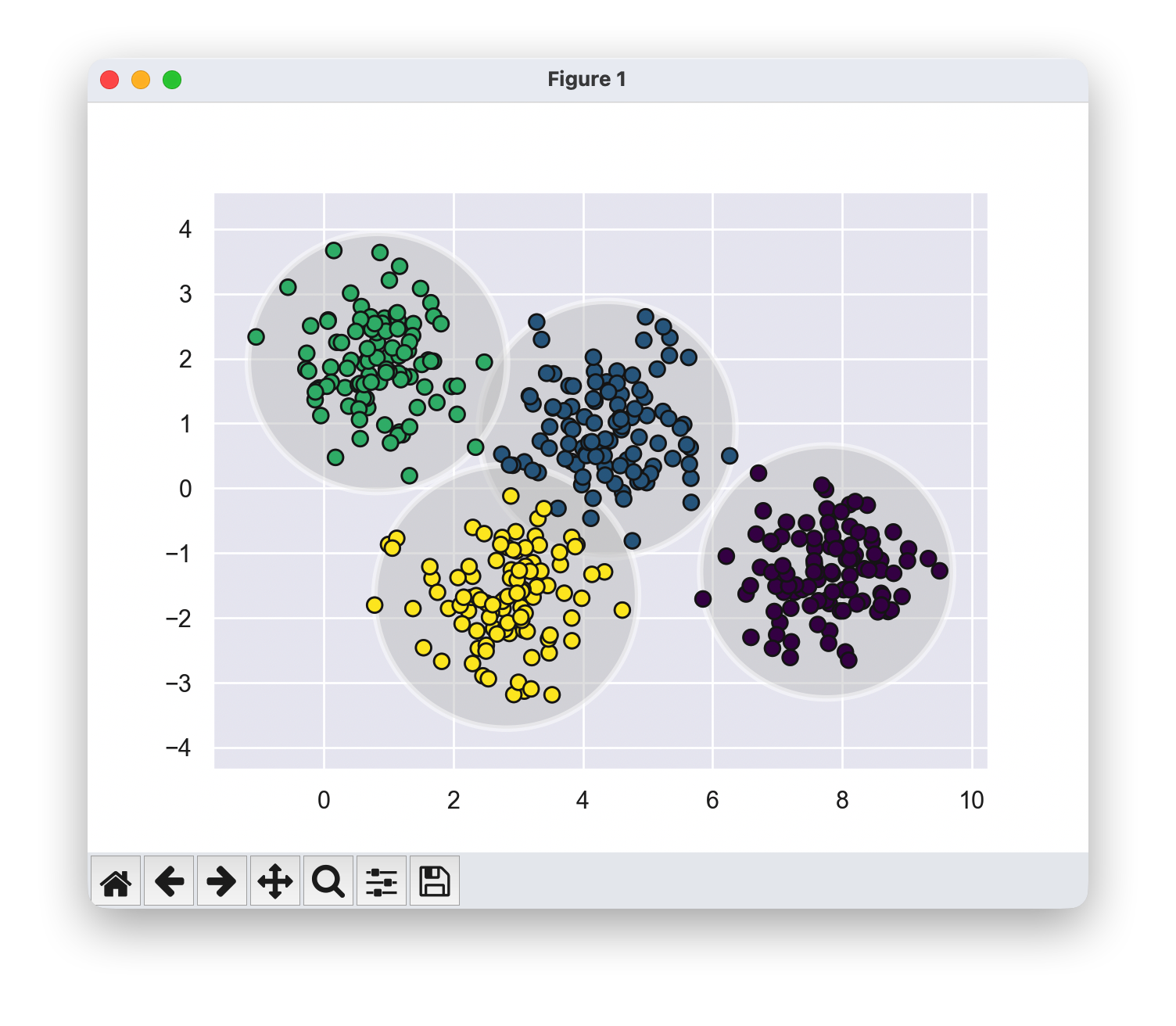
k-means在处理非圆形数据块时会失败
两个中间聚类之间似乎存在非常轻微的重叠,这使得我们对它们之间的点的聚类分配没有完全的信心。不幸的是,k-means模型本身没有衡量聚类分配的概率或不确定性的内在方法。
对于k-means来说,这些聚类模型必须是圆形的。k-means没有内置的方法来考虑长条形或椭圆形的聚类。因此,例如,如果我们对相同的数据进行变换,聚类分配最终会变得混乱。
k-means不够灵活,无法考虑这种情况,而是试图强行将数据拟合到四个圆形聚类中。这导致聚类分配混合在一起,其中得到的圆形出现了重叠。
rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))
kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans, X_stretched)
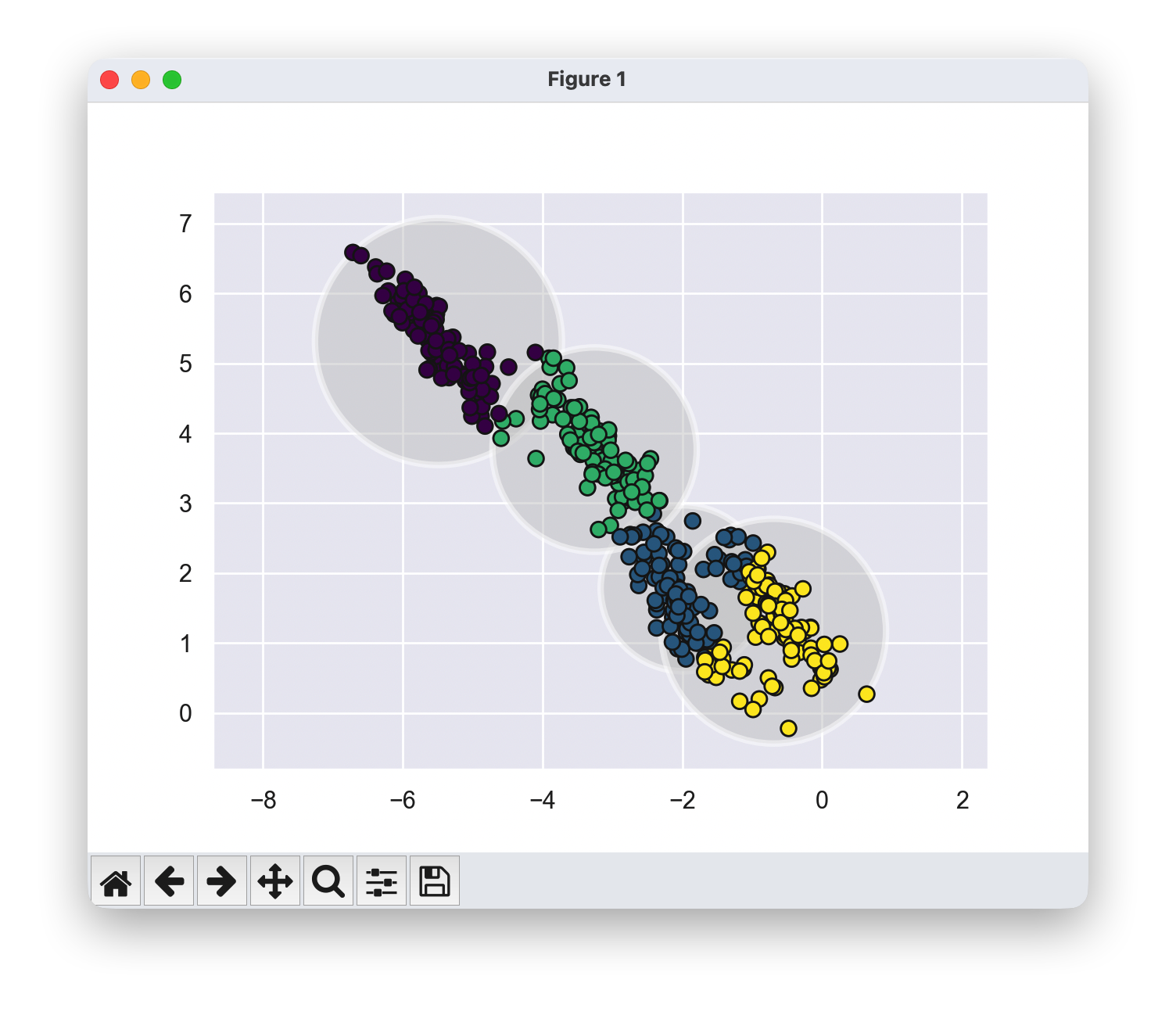
1.4 高斯混合模型绘制散点图
扩展到高斯混合模型(Gaussian Mixture Models, GMM)
你可能会想到两种改进方法:
- 你可以通过比较每个点到所有聚类中心的距离来衡量聚类分配中的不确定性,而不仅仅是关注最近的聚类中心。
- 你也可以考虑允许聚类边界是椭圆形而不是圆形,以适应非圆形的聚类。
高斯混合模型(Gaussian Mixture Model, GMM)尝试找到一组多维高斯概率分布,这些分布能够最好地拟合输入的数据集。在最简单的情况下,GMM 可以像 k-means 一样用于查找聚类。
然而,由于 GMM 内部包含一个概率模型,因此也可以找到概率性的聚类分配。在 Scikit-Learn 中,这可以通过 predict_proba 方法实现。该方法返回一个大小为 [n_samples, n_clusters] 的矩阵,表示每个样本属于某个聚类的概率。
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=4).fit(X)
labels = gmm.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis');

probs = gmm.predict_proba(X)
print(probs[:5].round(3))
1.5 通过将数据点的大小与概率成比例,可视化不确定性
size = probs.max(1)/0.02
plt.scatter(X[:, 0], X[:, 1], c=labels, edgecolor='k', cmap='viridis', s=size);
from matplotlib.patches import Ellipse
def draw_ellipse(position, covariance, ax=None, **kwargs):
"""Draw an ellipse with a given position and covariance"""
ax = ax or plt.gca()
if covariance.shape == (2, 2):
U, s, Vt = np.linalg.svd(covariance)
angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
width, height = 2 * np.sqrt(s)
else:
angle = 0
width, height = 2 * np.sqrt(covariance)
for nsig in range(1, 4):
ellipse = Ellipse(position, nsig * width, nsig * height, angle=angle, **kwargs)
ax.add_patch(ellipse)
def plot_gmm(gmm, X, label=True, ax=None):
ax = ax or plt.gca()
labels = gmm.fit(X).predict(X)
if label:
ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2,edgecolor='k')
else:
ax.scatter(X[:, 0], X[:, 1], s=40, zorder=2,edgecolor='k')
ax.axis('equal')
w_factor = 0.2 / gmm.weights_.max()
for pos, covar, w in zip(gmm.means_, gmm.covariances_, gmm.weights_):
draw_ellipse(pos, covar, alpha=w * w_factor)
gmm = GaussianMixture(n_components=4, covariance_type='full', random_state=42)
plot_gmm(gmm, X_stretched)
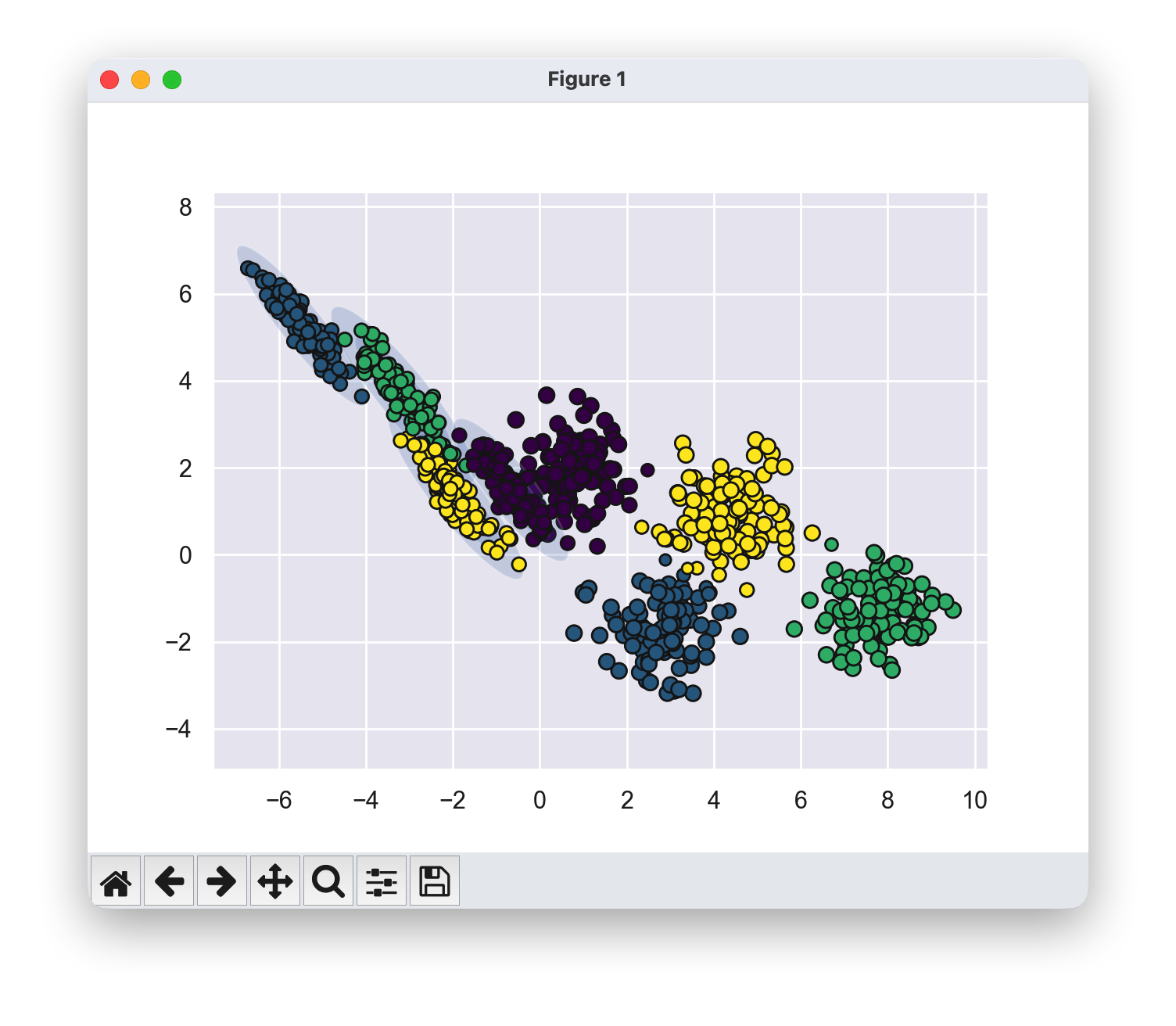
1.6 GMM作为密度估计和生成模型算法
尽管高斯混合模型(GMM)通常被归类为一种聚类算法,但从本质上讲,它是一种密度估计算法。也就是说,对某些数据拟合GMM的结果,从技术上讲并不是一个聚类模型,而是一个生成概率模型,用于描述数据的分布。
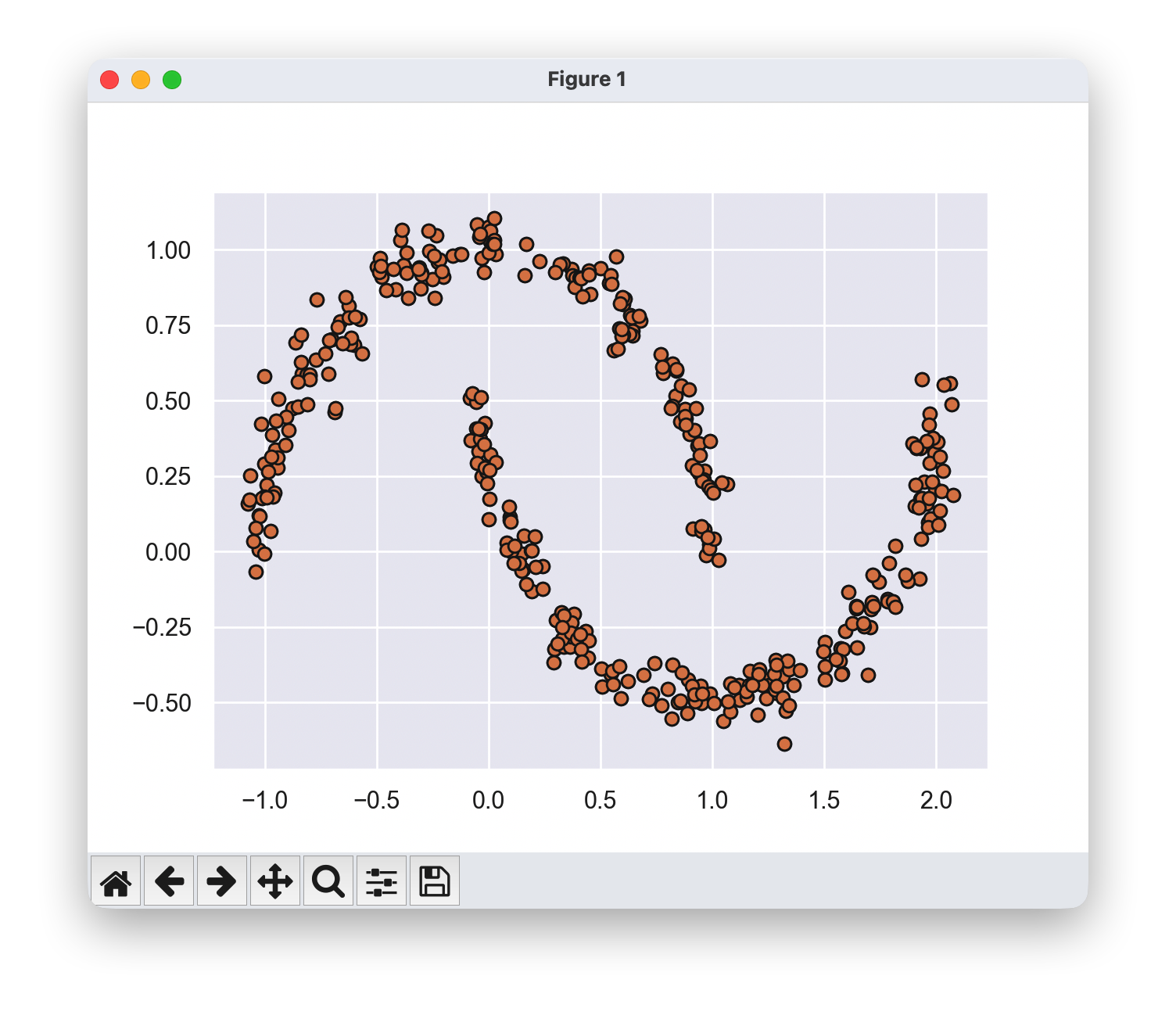
from sklearn.datasets import make_moons
Xmoon, ymoon = make_moons(200, noise=.05, random_state=0)
plt.scatter(Xmoon[:, 0], Xmoon[:, 1],edgecolor='k');
gmm2 = GaussianMixture(n_components=2, covariance_type='full', random_state=0)
plt.figure(figsize=(8,5))
plot_gmm(gmm2, Xmoon)
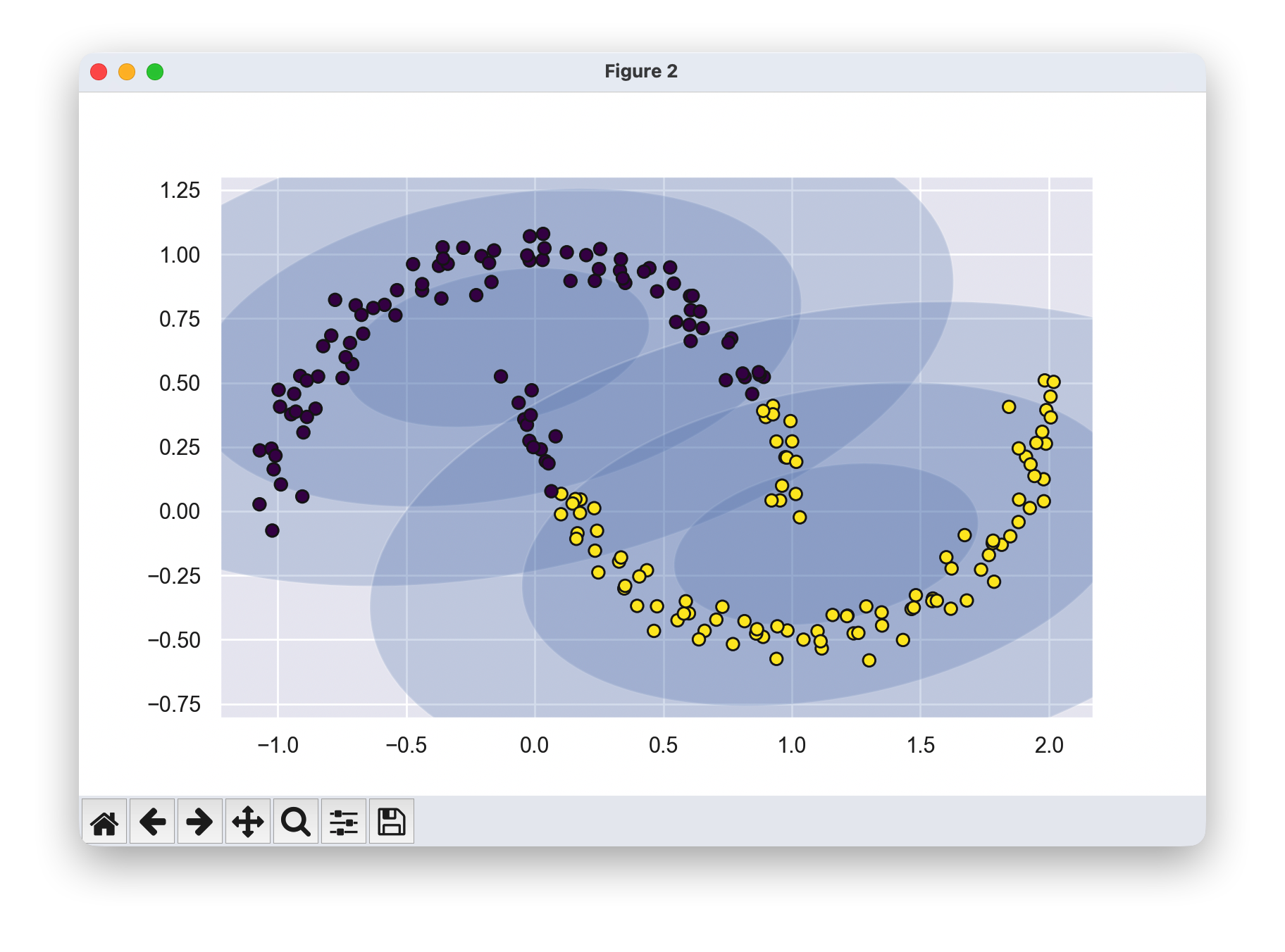
在这里,16个高斯分布的混合并不是为了找到分离的数据聚类,而是为了建模输入数据的总体分布。这是一个关于分布的生成模型,也就是说高斯混合模型(GMM)为我们提供了生成新的随机数据的配方,这些新数据的分布与我们的输入数据类似
gmm4 = GaussianMixture(n_components=4, covariance_type='full', random_state=0)
plot_gmm(gmm4, Xmoon, label=False)
gmm8 = GaussianMixture(n_components=8, covariance_type='full', random_state=0)
plot_gmm(gmm8, Xmoon, label=False)
gmm16 = GaussianMixture(n_components=16, covariance_type='full', random_state=0)
plot_gmm(gmm16, Xmoon, label=False)
Xnew,_ = gmm4.sample(400)
plt.scatter(Xnew[:, 0], Xnew[:, 1],edgecolor='k');
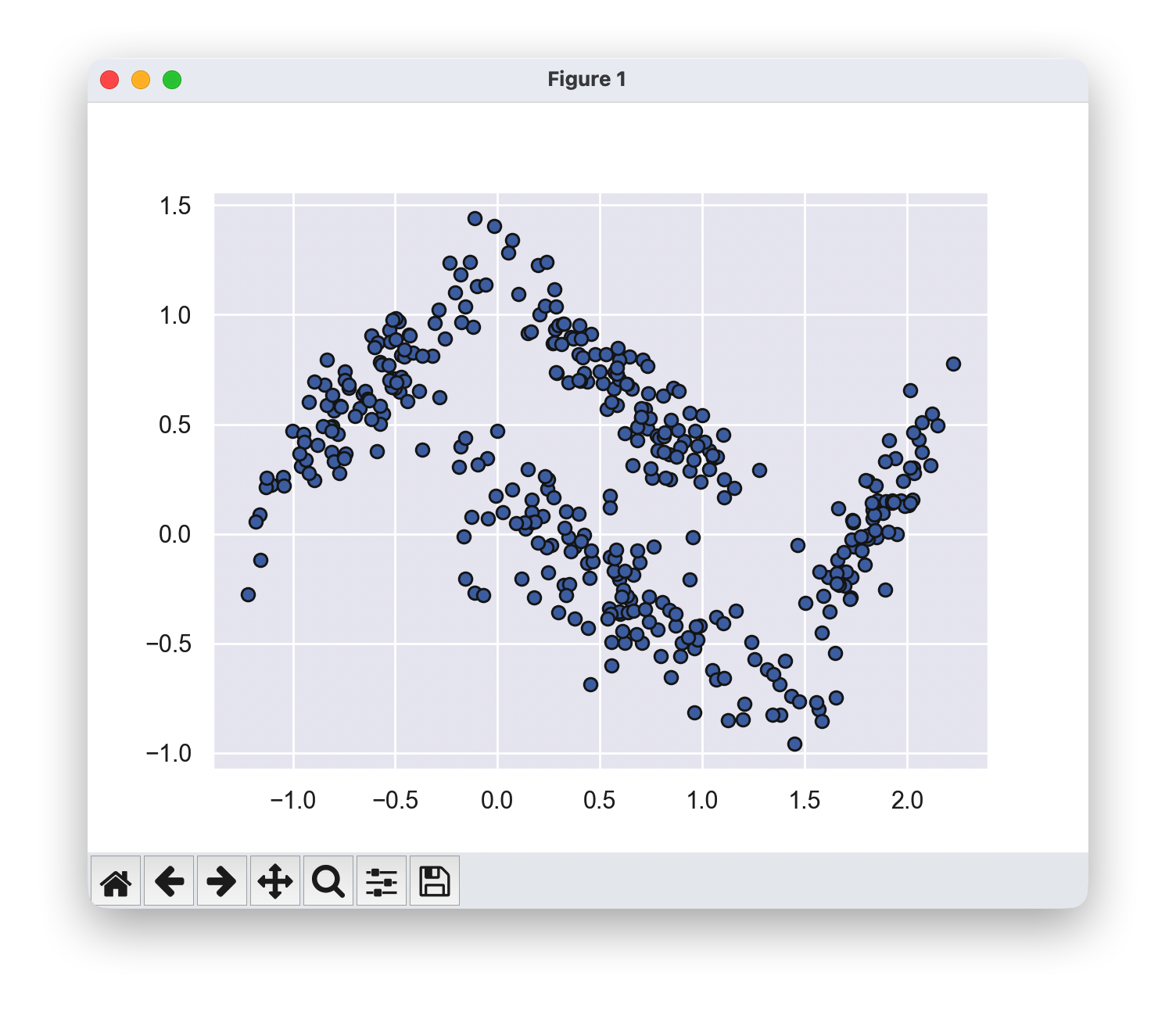
Xnew,_ = gmm8.sample(400)
plt.scatter(Xnew[:, 0], Xnew[:, 1],edgecolor='k');
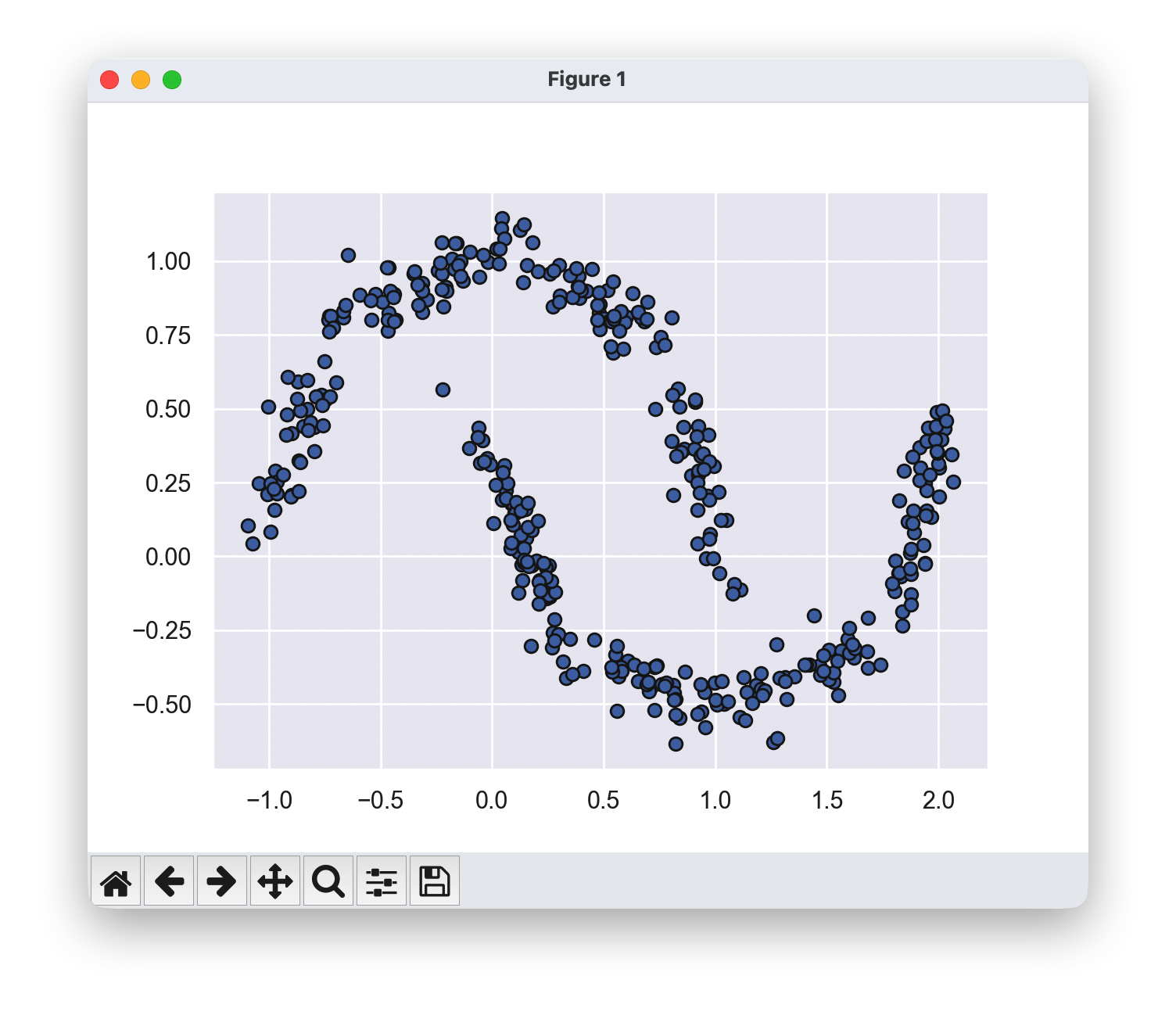
Xnew,_ = gmm16.sample(400)
plt.scatter(Xnew[:, 0], Xnew[:, 1],edgecolor='k');
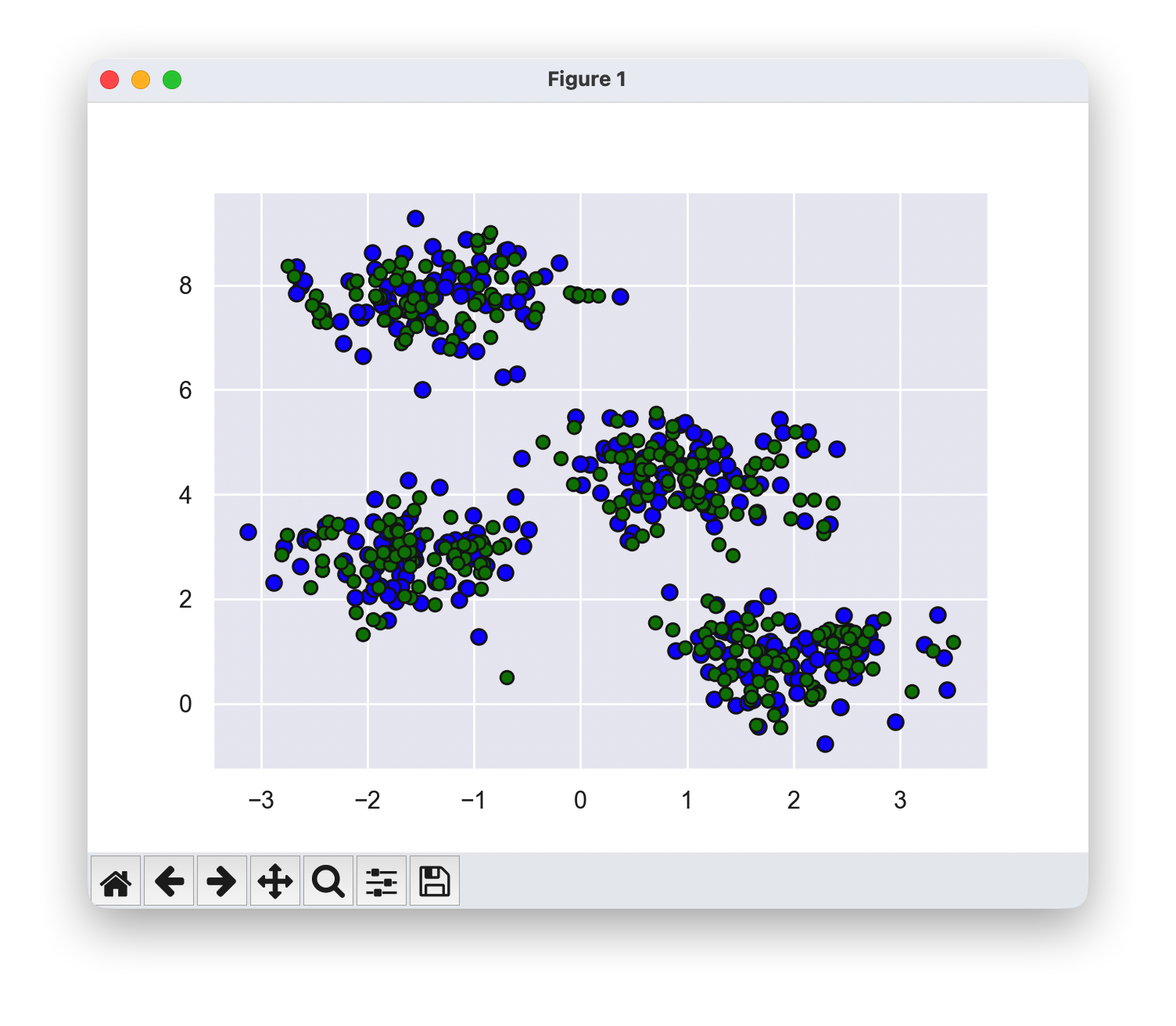
这种生成模型适用于任何类型的数据形状
X, y_true = make_blobs(n_samples=300, centers=4,
cluster_std=0.60, random_state=0)
plt.scatter(X[:, 0], X[:, 1], s=50,color='blue',edgecolor='k');
gmm_gen = GaussianMixture(n_components=16, covariance_type='full', random_state=0,tol=1e-6,max_iter=1000,n_init=10)
gmm_gen.fit(X)
Xnew,_ = gmm_gen.sample(300)
plt.scatter(Xnew[:, 0], Xnew[:, 1],color='green',edgecolor='k');
plt.show()






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








