聚类技术与应用：层次聚类

层次聚类

学习目标

本课程通过使用购物趋势数据集进行层次聚类，并且通过画图更直观的看各种指标。

相关知识点

• 层次聚类

学习内容

1 层次聚类

分裂法

在这种方法中，我们将所有的观测值分配到一个单一的聚类中，然后将该聚类划分为两个最不相似的聚类。最后，我们递归地对每个聚类进行操作，直到每个观测值都有一个聚类。

凝聚法

在这种方法中，我们将每个观测值分配到它自己的聚类中。然后，计算每个聚类之间的相似性（例如，距离），并合并两个最相似的聚类。最后，重复步骤2和3，直到只剩下一个聚类。

连接或距离矩阵

在进行任何聚类之前，需要确定包含每个点之间距离的接近度矩阵，使用距离函数来实现。然后，矩阵被更新以显示每个聚类之间的距离。以下三种方法在测量每个聚类之间的距离方面有所不同。

单链接

在单链接层次聚类中，两个聚类之间的距离被定义为每个聚类中两点之间的最短距离。例如，左侧聚类“r”和“s”之间的距离等于它们两个最近点之间的箭头长度。

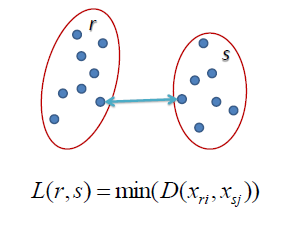
图1:单链接图

全链接

在全链接层次聚类中，两个聚类之间的距离被定义为每个聚类中两点之间的最长距离。例如，左侧聚类“r”和“s”之间的距离等于它们两个最远点之间的箭头长度。

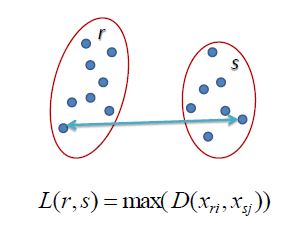
图2:全链接图

平均链接

在平均链接层次聚类中，两个聚类之间的距离被定义为一个聚类中的每个点与另一个聚类中的每个点之间的平均距离。例如，左侧聚类“r”和“s”之间的距离等于连接一个聚类中的点到另一个聚类中的点的每条箭头的平均长度。

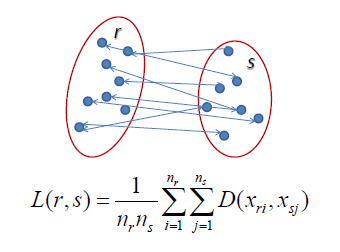
图3:平均链接图

树状图

树状图是树形图，通常用于说明层次聚类产生的聚类的排列。类群的排列根据它们的相似性（或不相似性）来确定。高度相近的类群彼此相似；高度不同的类群则不相似——高度差异越大，不相似性越高。

1.1 实验前准备

• 基于购物趋势数据集的聚类分析

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline

• 从obs桶中获取数据集

!wget https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_datasets/7ea3e3e2f28311ef9089fa163edcddae/Mall_Customers.zip
!unzip Mall_Customers.zip

• 读取数据集

df = pd.read_csv('Mall_Customers.csv')
df.head(10)
df.describe()

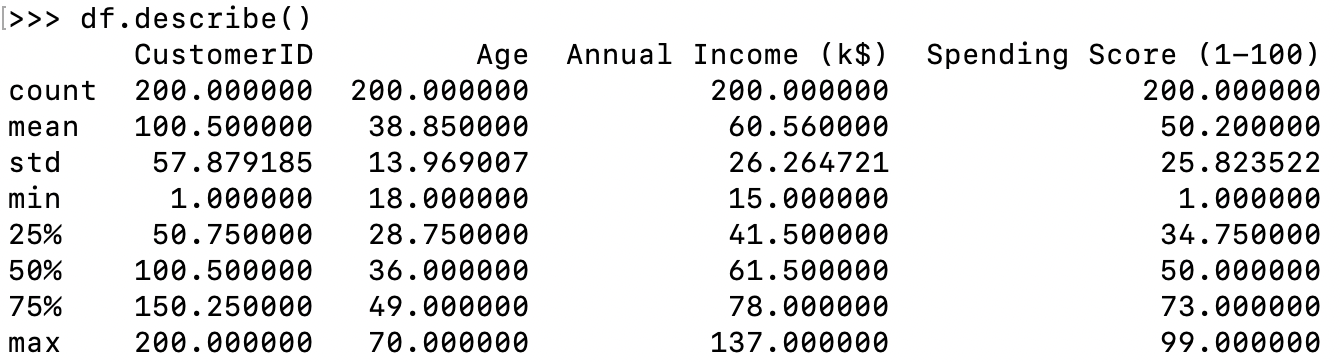
1.2 绘制收入支出的各类图像

• 绘制年收入分布图，使用直方图显示年收入的分布情况。

plt.figure(figsize=(8,5))
plt.title("Annual income distribution",fontsize=16)
plt.xlabel ("Annual income (k$)",fontsize=14)
plt.grid(True)
plt.hist(df['Annual Income (k$)'],color='orange',edgecolor='k')
plt.show()

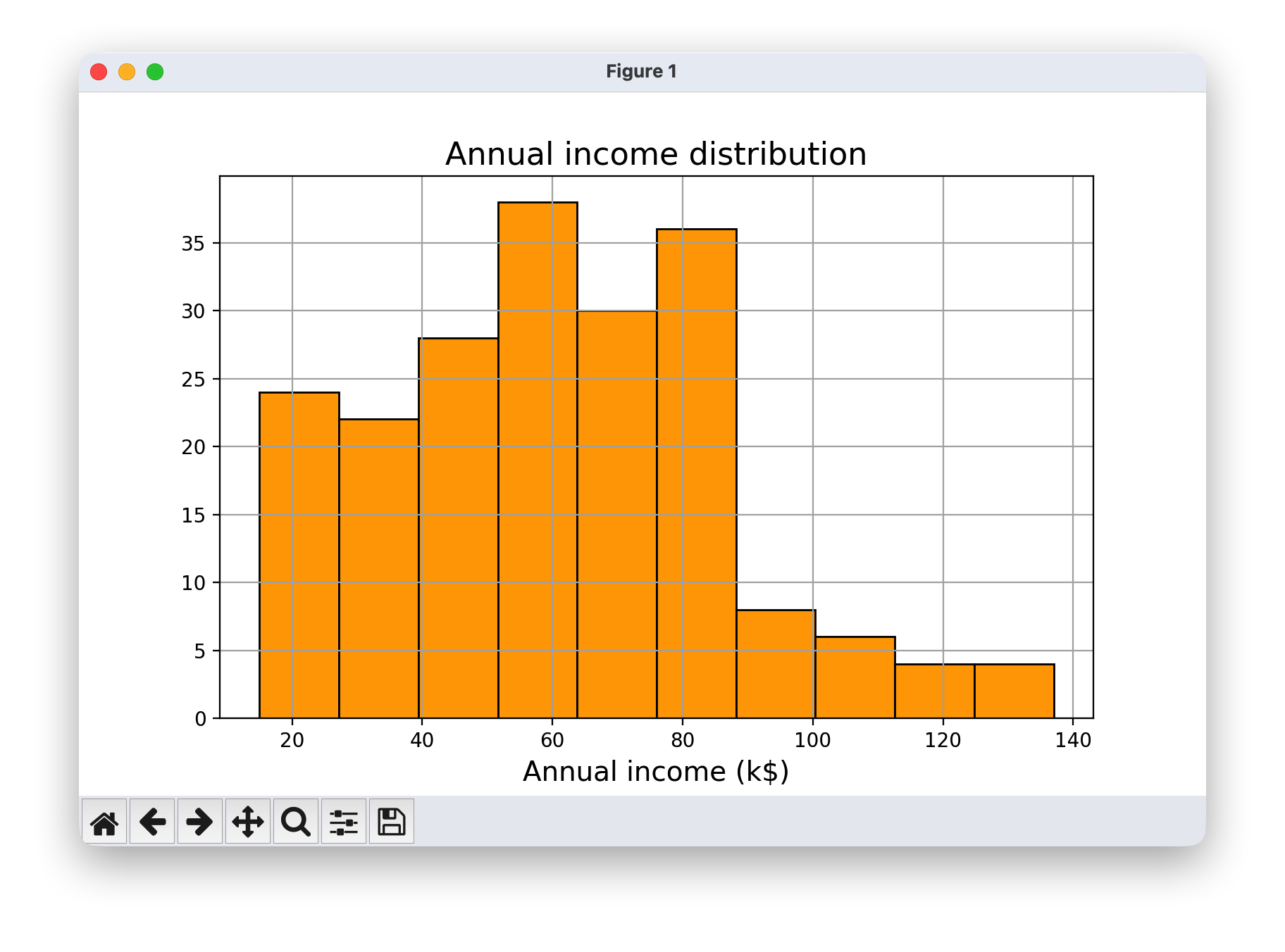
• 绘制支出得分分布图，使用直方图显示支出得分的分布情况。

plt.figure(figsize=(8,5))
plt.title("Spending Score distribution",fontsize=16)
plt.xlabel ("Spending Score (1-100)",fontsize=14)
plt.grid(True)
plt.hist(df['Spending Score (1-100)'],color='green',edgecolor='k')
plt.show()

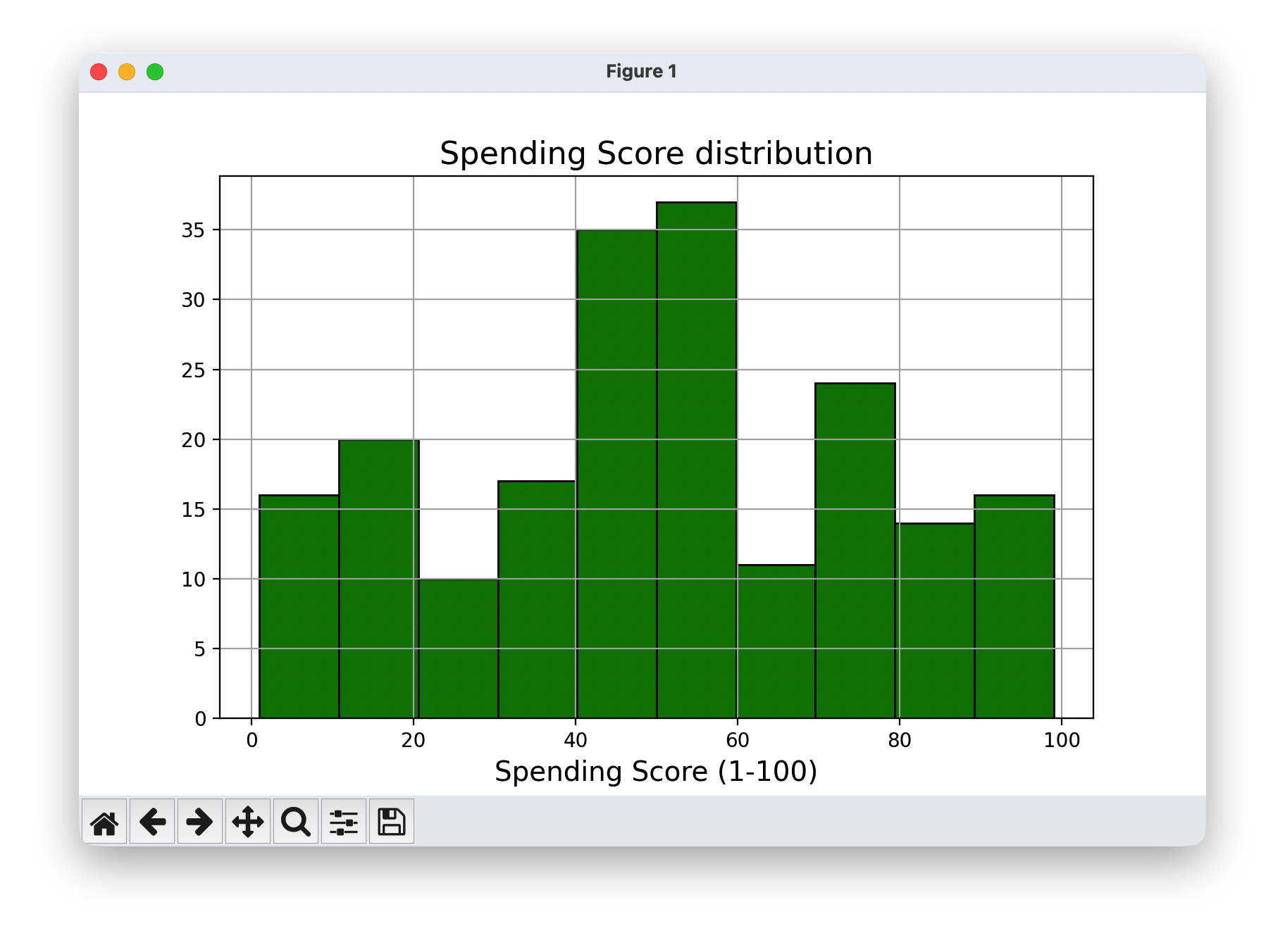
• 绘制年收入与消费评分的散点图，观察两者之间的相关性。

plt.figure(figsize=(8,5))
plt.title("Annual Income and Spending Score correlation",fontsize=18)
plt.xlabel ("Annual Income (k$)",fontsize=14)
plt.ylabel ("Spending Score (1-100)",fontsize=14)
plt.grid(True)
plt.scatter(df['Annual Income (k$)'],df['Spending Score (1-100)'],color='red',edgecolor='k',alpha=0.6, s=100)
plt.show()

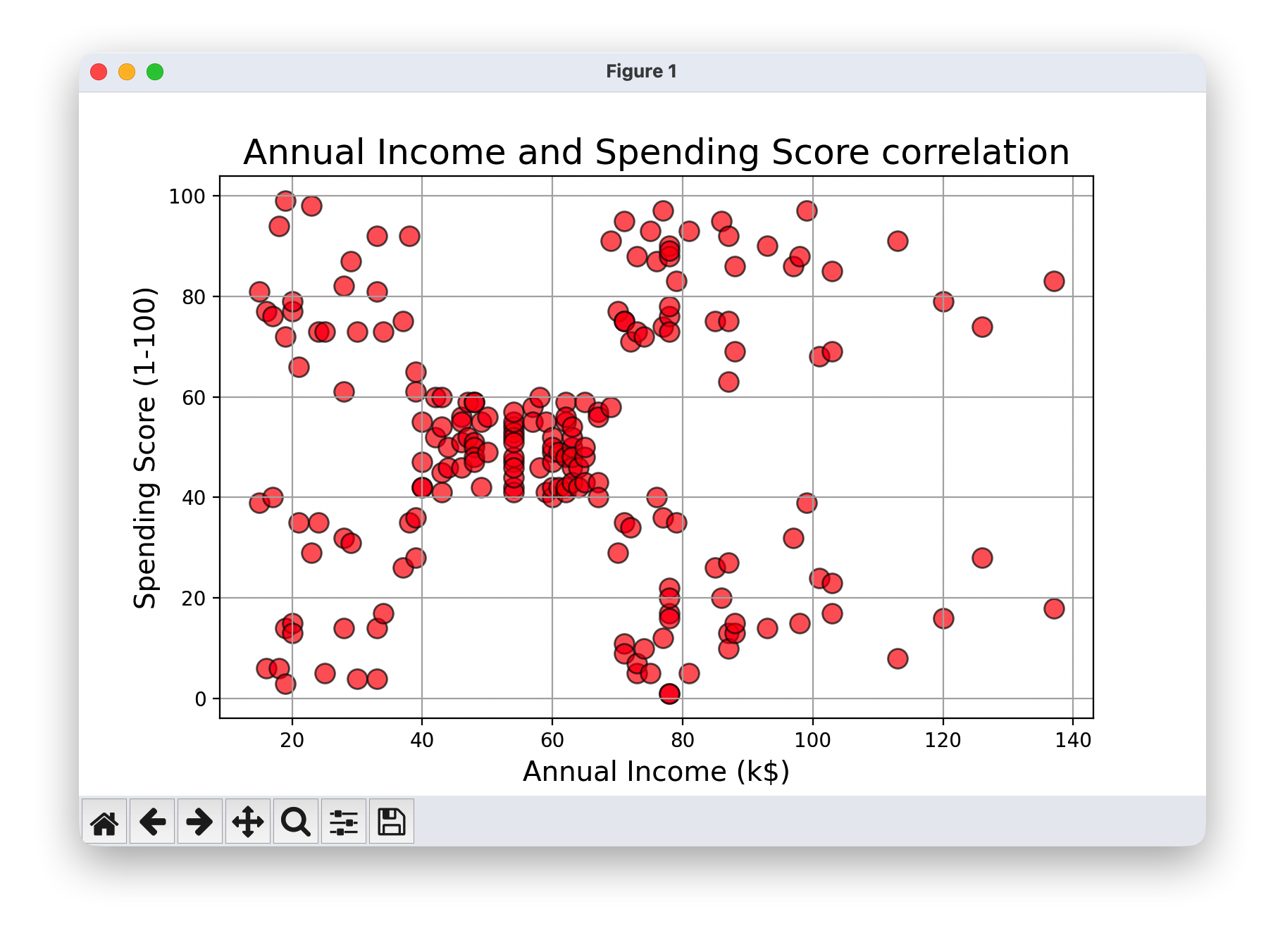
• 绘制年龄与支出得分的散点图，观察两者之间的相关性。

plt.figure(figsize=(8,5))
plt.title("Age and Spending Score correlation",fontsize=18)
plt.xlabel ("Age",fontsize=14)
plt.ylabel ("Spending Score (1-100)",fontsize=14)
plt.grid(True)
plt.scatter(df['Age'],df['Spending Score (1-100)'],color='blue',edgecolor='k',alpha=0.6, s=100)
plt.show()

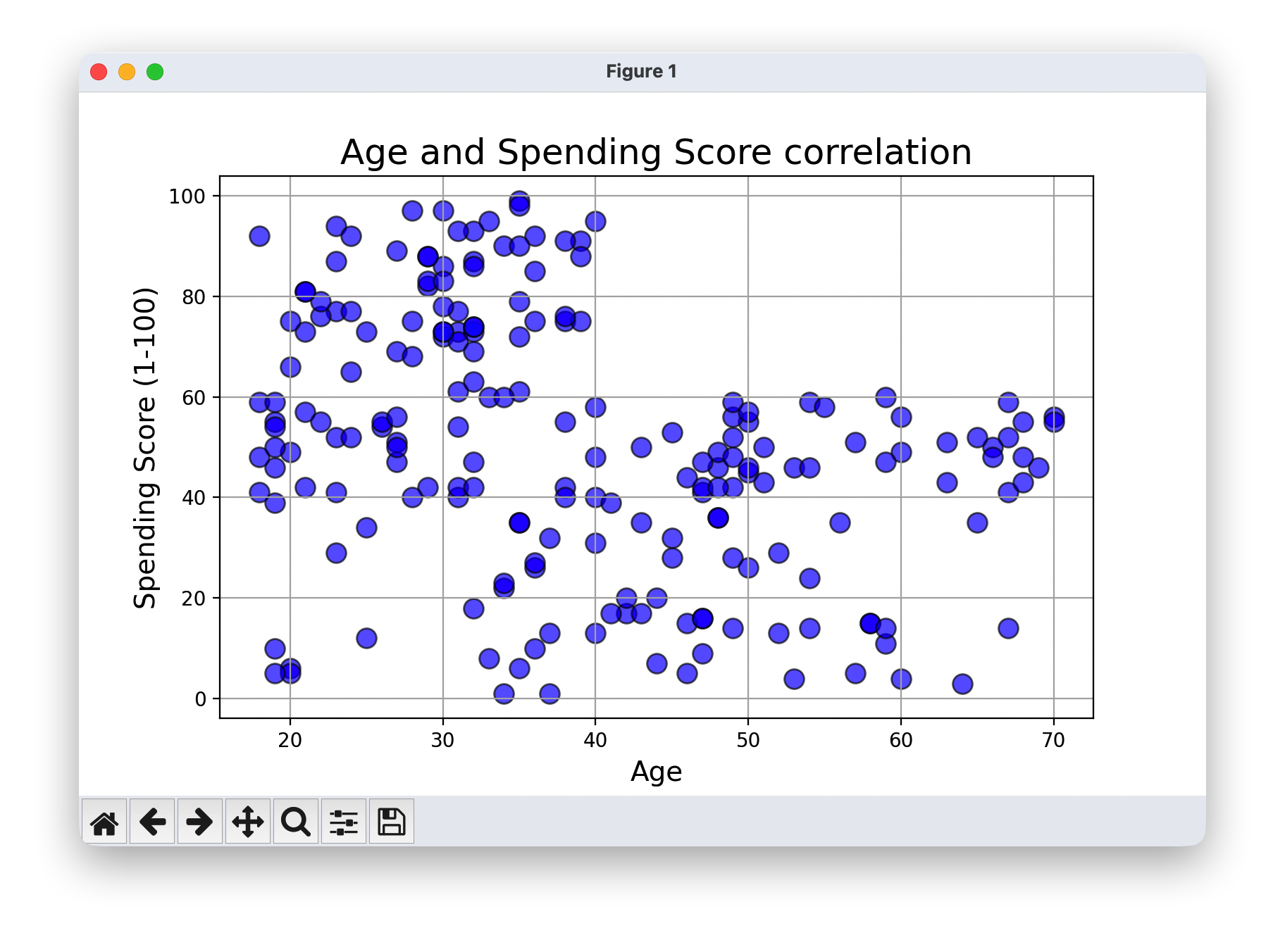
策略

因此，我们将基于客户的年收入和消费得分来探索聚类，看看是否存在可以区分的聚类，以便商场能够进行针对性的营销。

我们可以使用K均值聚类，但我们对隐藏的聚类数量没有任何概念。我们会发现，带有树状图的层次聚类可以为我们提供关于最佳聚类数量的良好见解。

X = df.iloc[:,[3,4]].values

Ward 距离矩阵

我们将使用“Ward”距离矩阵来构建这个树状图。
$$d(u,v)=\sqrt{\frac{|v|+|s|}{T}d(v,s{)}^2+\frac{|v|+|t|}{T}d(v,t{)}^2-\frac{|v|}{T}d(s,t{)}^2}$$

其中， $u$ 是由聚类 $s$ 和 $t$ 新合并而成的聚类， $v$ 是森林中尚未使用的聚类， $T=|v|+|s|+|t|$ ，而 $|\ast |$ 表示其参数的基数。这被称为增量算法。

import scipy.cluster.hierarchy as sch

plt.figure(figsize=(15,6))
plt.title('Dendrogram')
plt.xlabel('Customers')
plt.ylabel('Euclidean distances')
dendrogram = sch.dendrogram(sch.linkage(X, method = 'ward'))
plt.show()

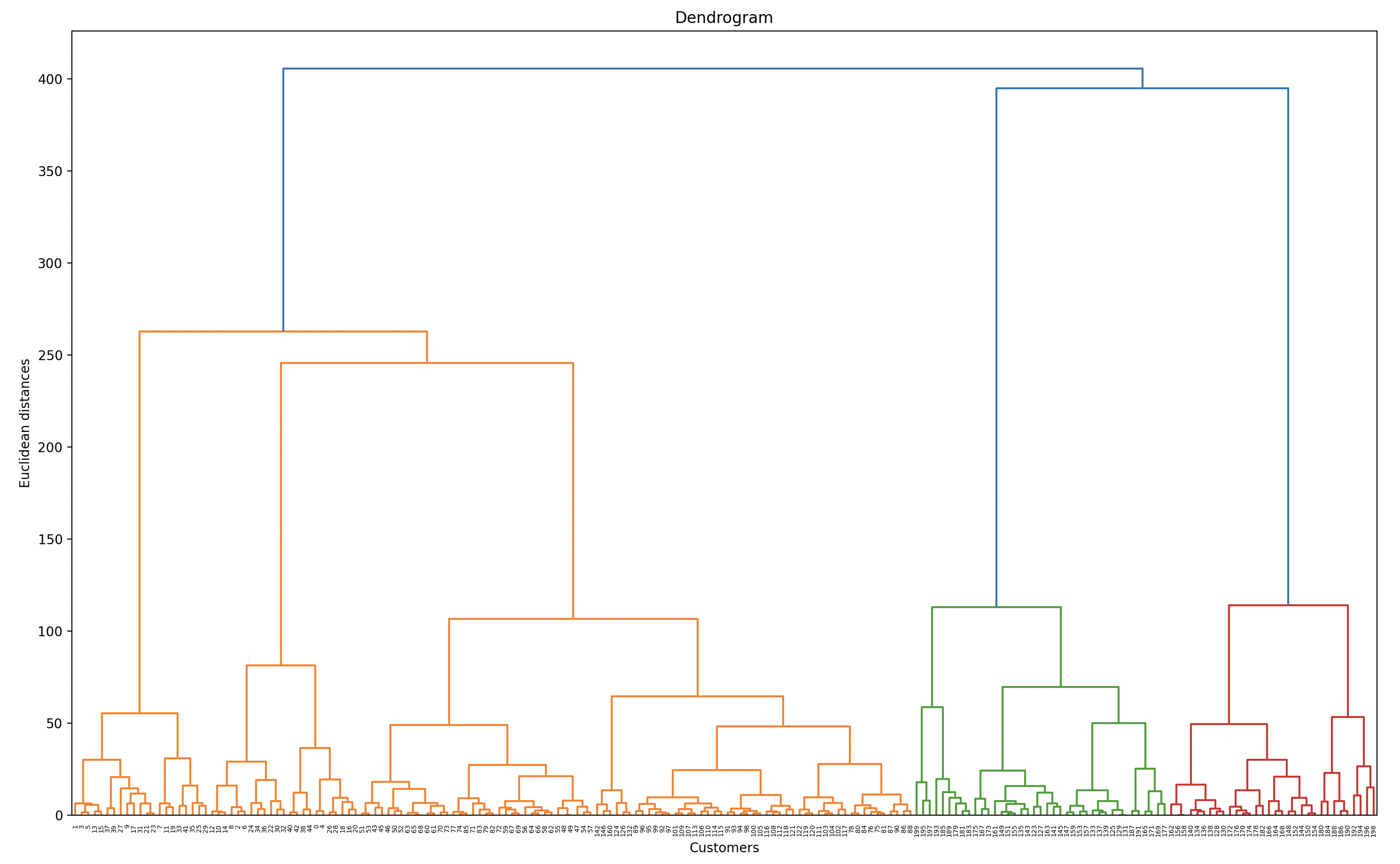
最佳聚类数量

通常，可以通过查看树状图（Dendrogram）以一种简单的方式找到最佳聚类数量。

• 寻找最长的一段垂直线，这段线没有被任何“延伸”的水平线（这里的“延伸”是指将聚类分隔线无限延伸到两个方向）穿过。
• 在这段线上选择任意一点，并画一条假想的水平线。
• 统计这条假想的水平线穿过了多少条垂直线。
• 这个数字很可能是最佳的聚类数量。

这个想法在下图中展示。在这里，最佳聚类数量可能是5。

plt.figure(figsize=(15,6))
plt.title('Dendrogram')
plt.xlabel('Customers')
plt.ylabel('Euclidean distances')
plt.hlines(y=190,xmin=0,xmax=2000,lw=3,linestyles='--')
plt.text(x=900,y=220,s='Horizontal line crossing 5 vertical lines',fontsize=20)
#plt.grid(True)
dendrogram = sch.dendrogram(sch.linkage(X, method = 'ward'))
plt.show()

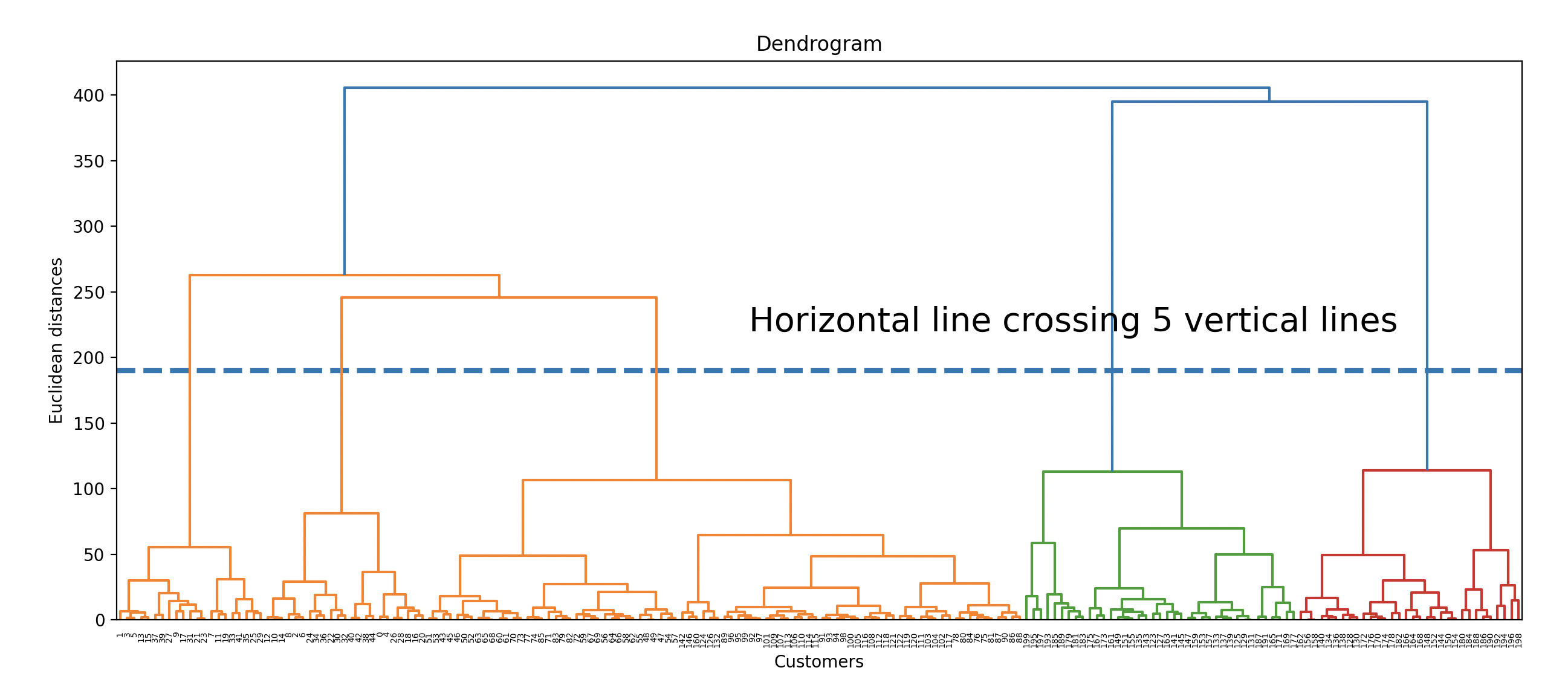
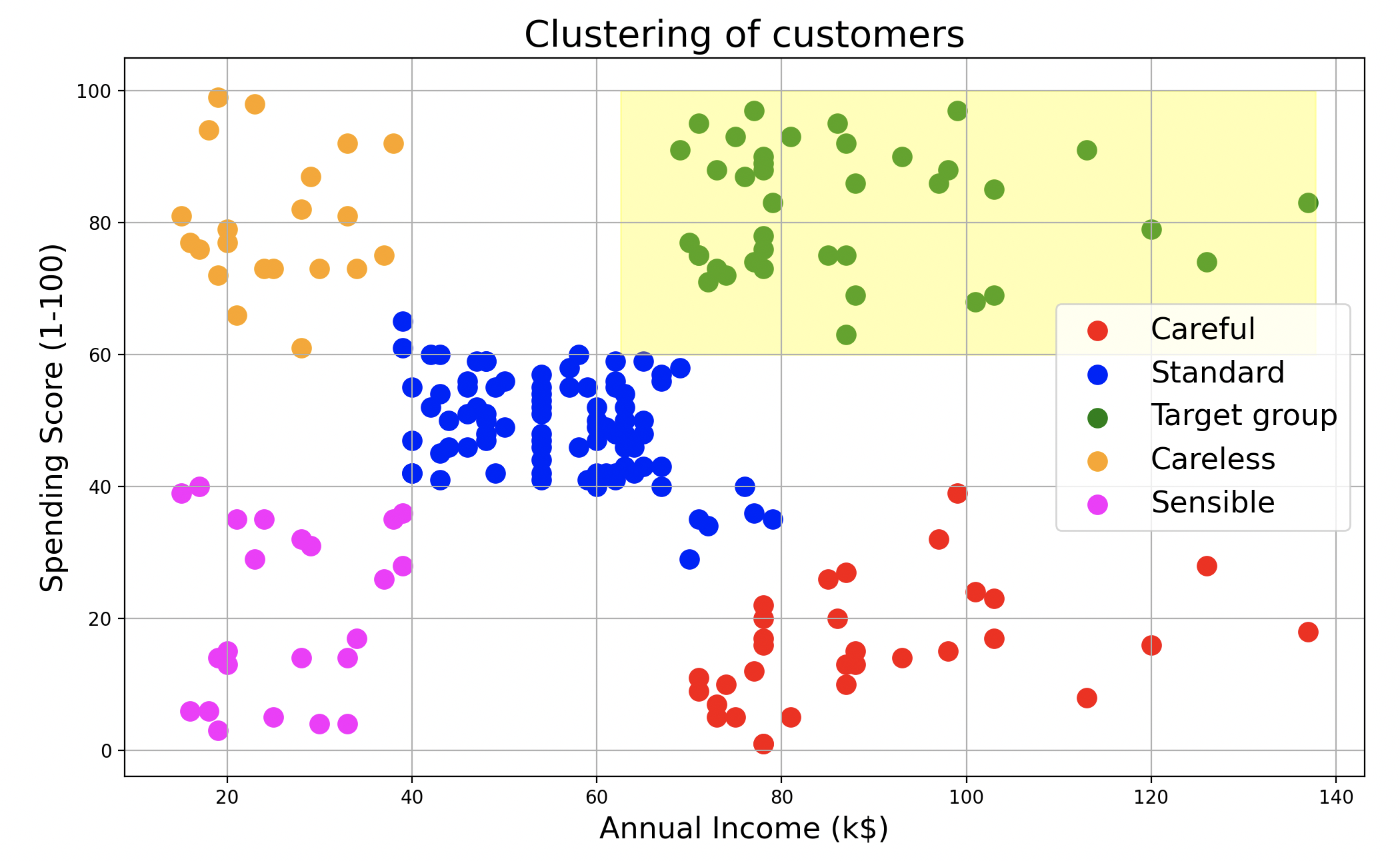
绘制集群并标记客户类型

• Careful - 高收入但低消费者
• Standard - 中等收入和中等消费者
• Target group - 高收入和高消费者（应为商场的目标）
• Careless - 低收入但高消费者（应避免，因为可能存在信用风险）
• Sensible - 低收入和低消费者

1.3 构建模型并绘制聚类结果

• 绘制聚类结果（创建一个图形窗口，设置图形大小为宽12英寸、高7英寸。）

#导入聚类模型
from sklearn.cluster import AgglomerativeClustering
#创建聚类模型
hc = AgglomerativeClustering(n_clusters=5, metric='euclidean', linkage='ward')
y_hc = hc.fit_predict(X)
plt.figure(figsize=(12,7))
plt.scatter(X[y_hc == 0, 0], X[y_hc == 0, 1], s = 100, c = 'red', label = 'Careful')
plt.scatter(X[y_hc == 1, 0], X[y_hc == 1, 1], s = 100, c = 'blue', label = 'Standard')
plt.scatter(X[y_hc == 2, 0], X[y_hc == 2, 1], s = 100, c = 'green', label = 'Target group')
plt.scatter(X[y_hc == 3, 0], X[y_hc == 3, 1], s = 100, c = 'orange', label = 'Careless')
plt.scatter(X[y_hc == 4, 0], X[y_hc == 4, 1], s = 100, c = 'magenta', label = 'Sensible')
plt.title('Clustering of customers',fontsize=20)
plt.xlabel('Annual Income (k$)',fontsize=16)
plt.ylabel('Spending Score (1-100)',fontsize=16)
plt.legend(fontsize=16)
plt.grid(True)
plt.axhspan(ymin=60,ymax=100,xmin=0.4,xmax=0.96,alpha=0.3,color='yellow')
plt.show()

通过k-means算法验证最佳聚类数量

给定一组观测值 $(x_1,x_2,\dots ,x_n)$，其中每个观测值是一个 d 维实向量，k-means 聚类（K-means clustering）的目标是将这 $n$ 个观测值划分为 $k$ (≤ $n$) 个集合 $S=S_1,S_2,\dots ,S_k$ ，以最小化每个聚类内的平方和（WCSS，即方差）。形式上，目标是找到：

$$\underset{\mathbf{S}}{\mathrm{argmin}}\sum _{i=1}^k\sum _{\mathbf{x}\in S_i}{\Vert \mathbf{x}-{\mathbf{\mu }}_i\Vert }^2=\underset{\mathbf{S}}{\mathrm{argmin}}\sum _{i=1}^k|S_i|\mathrm{Var}{S}_i$$

其中，${\mu }_i$ 是集合 $S_i$中点的均值。

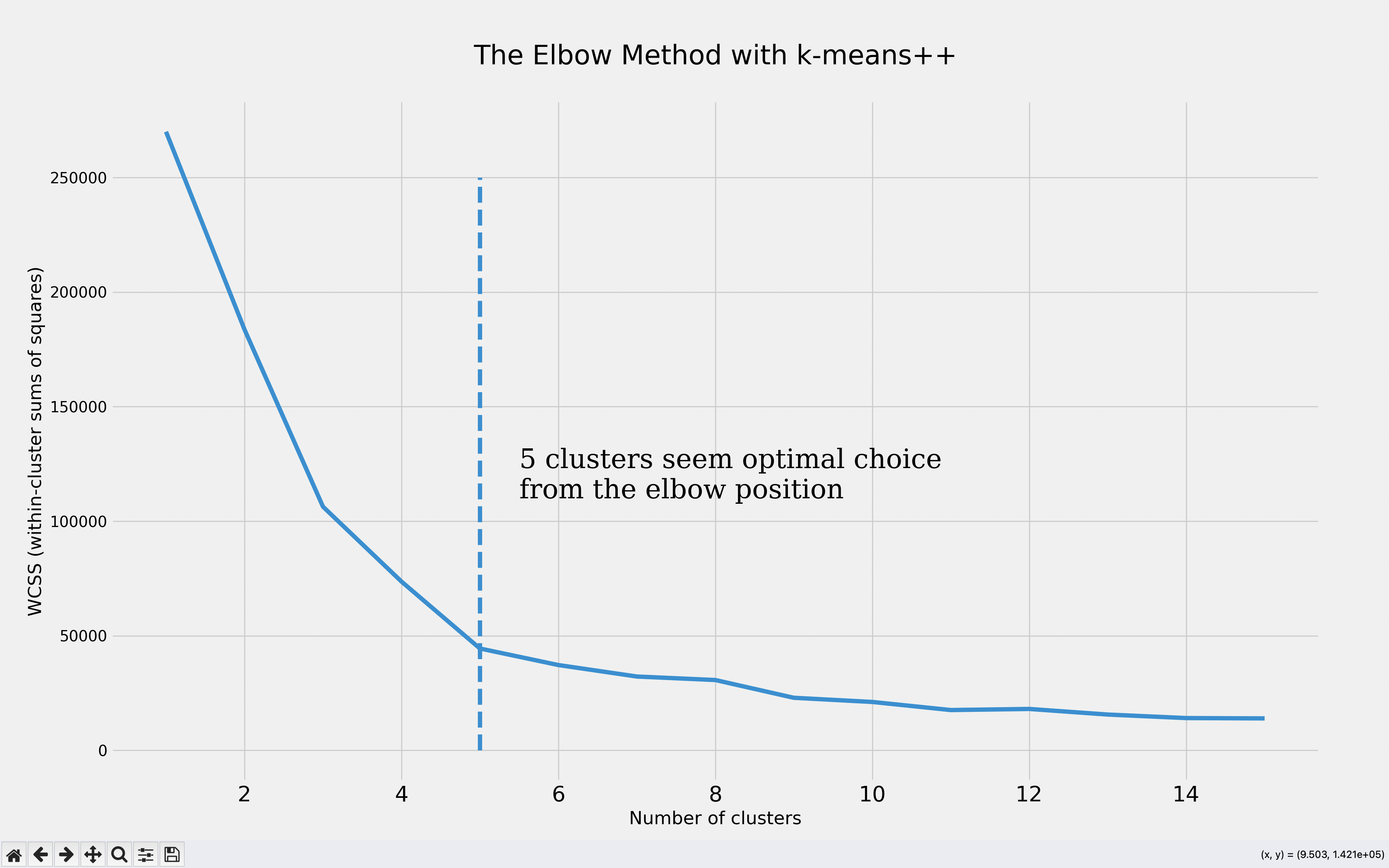
我们运行 k-means++ 模型（经过精心初始化质心的 k-means），迭代聚类数量（1 到 15），并绘制 聚类内平方和（WCSS）指标 图表，通过肘部法则确定最佳聚类数量。

from sklearn.cluster import KMeans
wcss = []
for i in range(1, 16):
    kmeans = KMeans(n_clusters = i, init = 'k-means++')
    kmeans.fit(X)
    wcss.append(kmeans.inertia_)
with plt.style.context(('fivethirtyeight')):
    plt.figure(figsize=(10,6))
    plt.plot(range(1, 16), wcss)
    plt.title('The Elbow Method with k-means++\n',fontsize=25)
    plt.xlabel('Number of clusters')
    plt.xticks(fontsize=20)
    plt.ylabel('WCSS (within-cluster sums of squares)')
    plt.vlines(x=5,ymin=0,ymax=250000,linestyles='--')
    plt.text(x=5.5,y=110000,s='5 clusters seem optimal choice \nfrom the elbow position',
             fontsize=25,fontdict={'family':'serif'})
    plt.show()