聚类技术与应用：DBSCAN聚类

最新推荐文章于 2025-12-16 15:16:39 发布

原创最新推荐文章于 2025-12-16 15:16:39 发布 · 1.5k 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#聚类 #数据挖掘 #机器学习 #DBSCAN聚类

DBSCAN聚类

学习目标

本课程将详细介绍DBSCAN聚类中的月亮形状和甜甜圈形状的数据制作和测试DBSCAN的性能，帮助学员理解其在神经网络训练中的应用。

学习内容

1 DBSCAN聚类

DBSCAN的算法原理是从一个未被访问过的任意对象开始，找到其 eps 邻域内的所有对象。如果该邻域内的对象数量大于等于 minPts，则将该对象标记为核心对象，并以该核心对象为起始点，继续扩展其密度相连的区域，将所有密度相连的对象都划分为同一个簇。重复这个过程，直到所有的对象都被访问过。

核心概念：

密度相连：如果存在一个对象链，链中的每个对象到其直接后继对象的距离都小于等于给定的距离阈值（eps），则称这些对象是密度相连的。
核心对象：一个对象如果在其给定半径 eps 的邻域内包含的对象数量大于等于最小样本数（minPts），则该对象被称为核心对象。
边界对象：处于核心对象的密度相连区域内，但本身不是核心对象的对象。
噪声点：既不是核心对象也不是边界对象的点。

1.1 导入库

import numpy as np
import matplotlib.pyplot as plt

1.2 制作月亮形状和甜甜圈形状的数据

在机器学习和数据可视化领域，我们经常需要使用具有特定几何特征的合成数据集来测试算法性能或展示可视化效果。本文介绍如何使用 Python 的 scikit-learn 库生成两种经典形状的数据集：月亮形状（半环形）和甜甜圈形状（同心圆）。
我们使用 scikit-learn 提供的两个专用函数来创建这些特殊形状的数据：

datasets.make_moons() - 生成两个交错的半月亮形状的点集。
datasets.make_circles() - 生成两个同心圆形的点集。
这些函数允许我们通过参数控制样本数量、噪声水平和形状特征，为实验提供灵活的数据来源。

from sklearn import cluster, datasets
n_samples = 1500
noisy_circles,circle_labels = datasets.make_circles(n_samples=n_samples, factor=.5,
                                      noise=.05)
noisy_moons,moon_labels = datasets.make_moons(n_samples=n_samples, noise=.1)
noisy_moons=np.array(noisy_moons)
noisy_circles = np.array(noisy_circles)

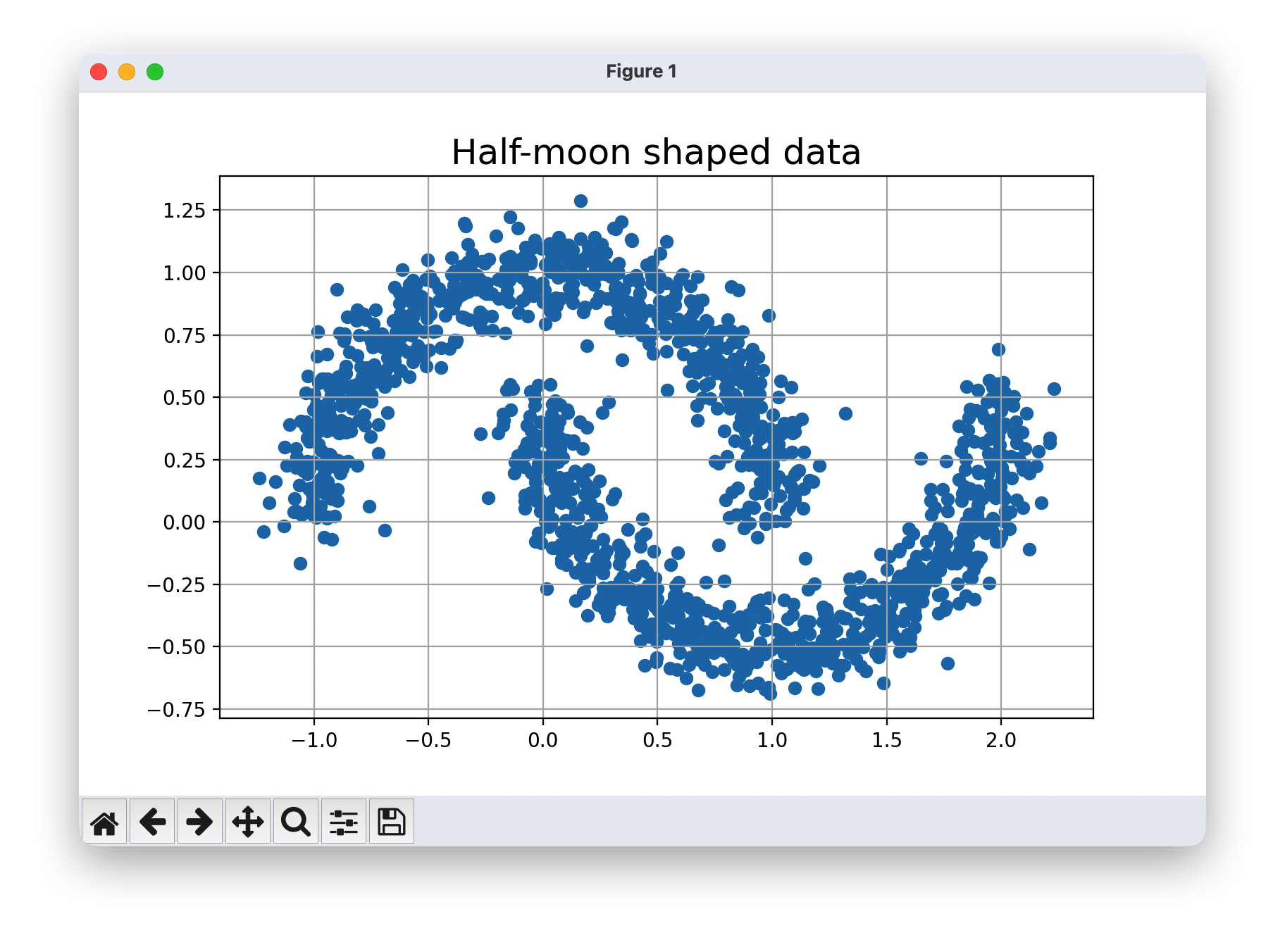
plt.figure(figsize=(8,5))
plt.title("Half-moon shaped data", fontsize=18)
plt.grid(True)
plt.scatter(noisy_moons[:,0],noisy_moons[:,1])
plt.show()

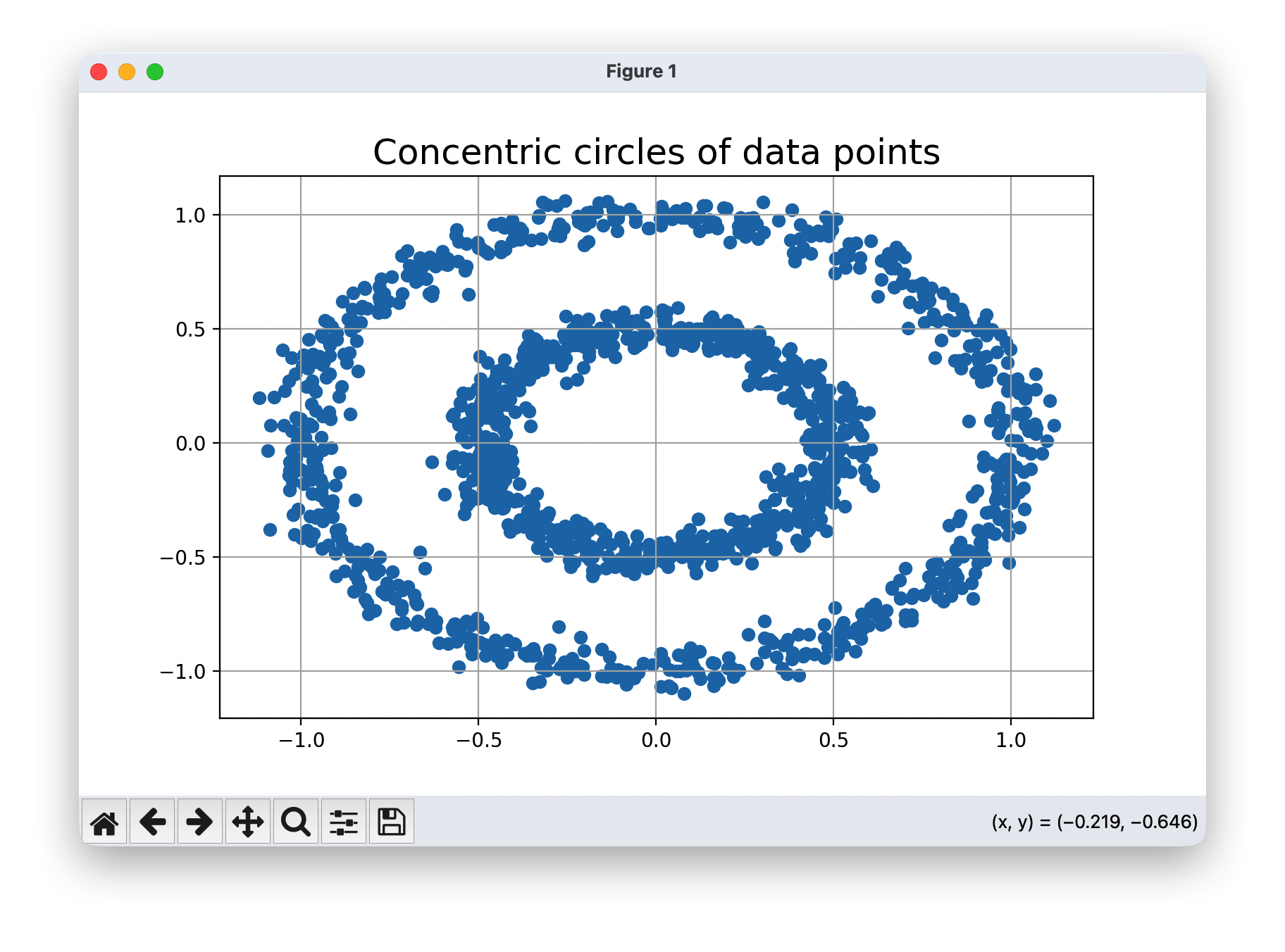
在这里插入图片描述

plt.figure(figsize=(8,5))
plt.title("Concentric circles of data points", fontsize=18)
plt.grid(True)
plt.scatter(noisy_circles[:,0],noisy_circles[:,1])
plt.show()

在这里插入图片描述

1.3 k-means识别正确的聚类

在数据聚类任务中，K-means 算法是应用最广泛的方法之一，但其基于距离的聚类逻辑使其在处理非凸形状数据时存在局限性。本课程通过分析 K-means 在月亮形状和甜甜圈形状数据上的聚类效果，展示该算法的优势与不足。

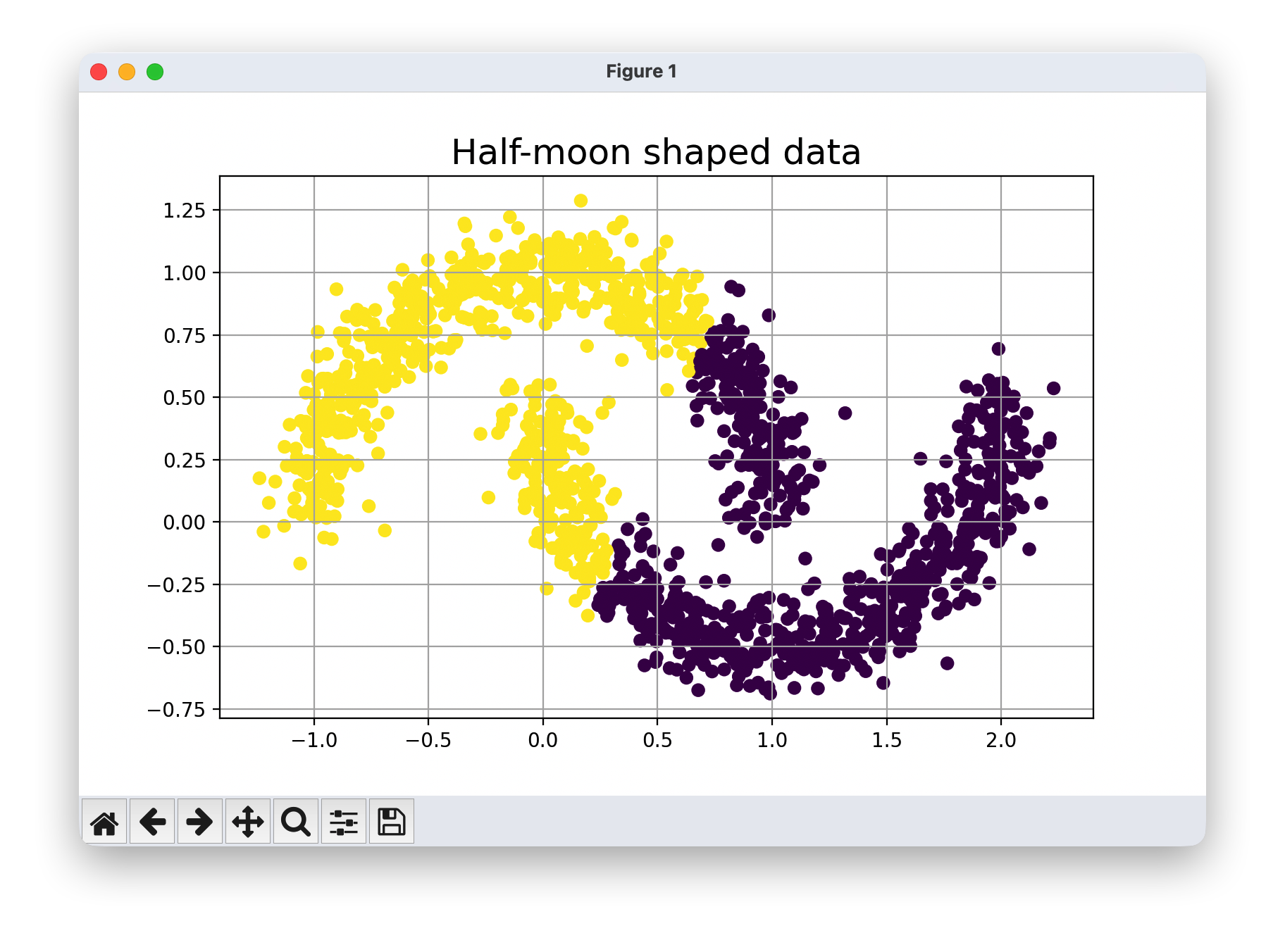
km=cluster.KMeans(n_clusters=2)
km.fit(noisy_moons)
plt.figure(figsize=(8,5))
plt.title("Half-moon shaped data", fontsize=18)
plt.grid(True)
plt.scatter(noisy_moons[:,0],noisy_moons[:,1],c=km.labels_)
plt.show()

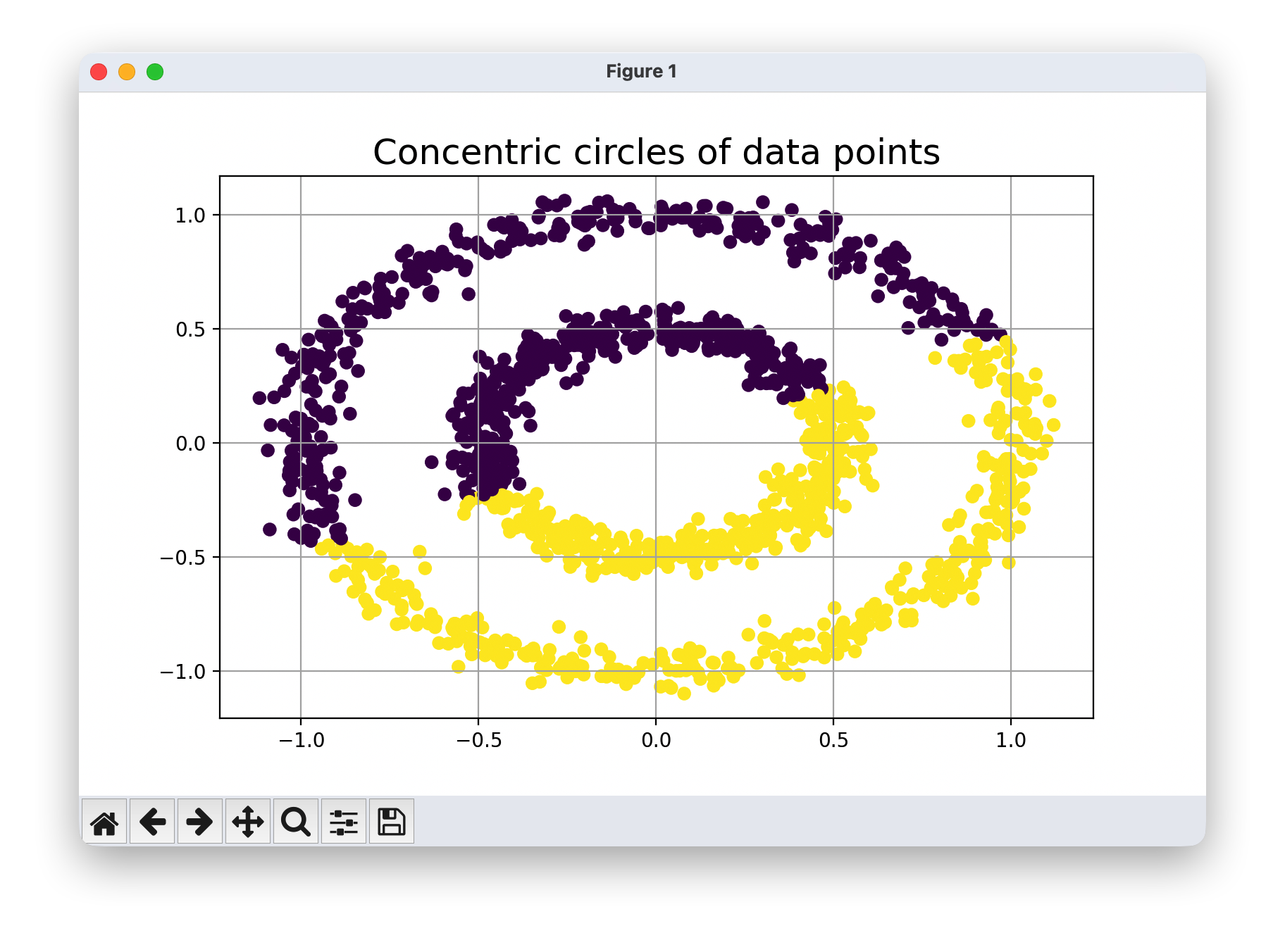
在这里插入图片描述

km.fit(noisy_circles)
plt.figure(figsize=(8,5))
plt.title("Concentric circles of data points", fontsize=18)
plt.grid(True)
plt.scatter(noisy_circles[:,0],noisy_circles[:,1],c=km.labels_)
plt.show()

在这里插入图片描述
从上述结果对比发现

1.月亮形状数据的聚类结果：

K-means 将数据分为上下两部分，而非按两个月牙形状分开。
这是因为 K-means 无法识别数据的非线性边界，只能通过直线划分空间。
此案例揭示了 K-means 在处理非凸形状聚类时的局限性。

2.甜甜圈形状数据的聚类结果：

K-means 无法区分内外两个圆圈，通常会沿直径将数据分成两半。
算法无法理解数据的环形结构，因为其基于欧氏距离的聚类机制无法捕捉这种嵌套关系。

1.4 DBSCAN的性能分析

DBSCAN 算法基于数据点的密度来进行聚类。其核心概念包括：

核心点：在给定的邻域半径eps内包含至少min_samples个点的数据点。
边界点：在eps邻域内包含的点数少于min_samples，但落在核心点的邻域内的数据点。
噪声点：既不是核心点也不是边界点的数据点。

算法通过不断扩展核心点的邻域来形成聚类，直到所有的数据点都被访问过。

dbs = cluster.DBSCAN(eps=0.1)
dbs.fit(noisy_moons)
plt.figure(figsize=(8,5))
plt.title("Half-moon shaped data", fontsize=18)
plt.grid(True)
plt.scatter(noisy_moons[:,0],noisy_moons[:,1],c=dbs.labels_)
plt.show()

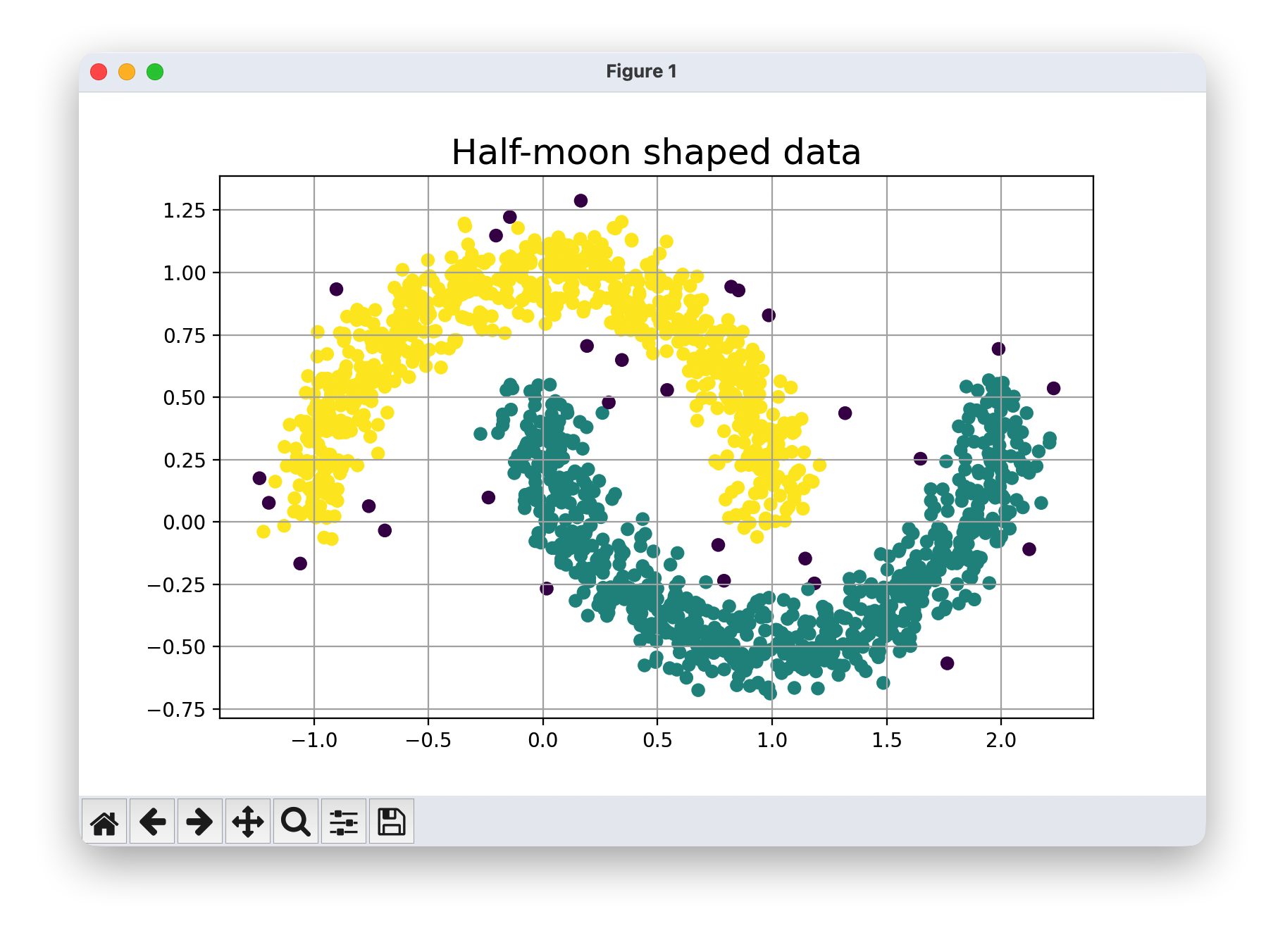
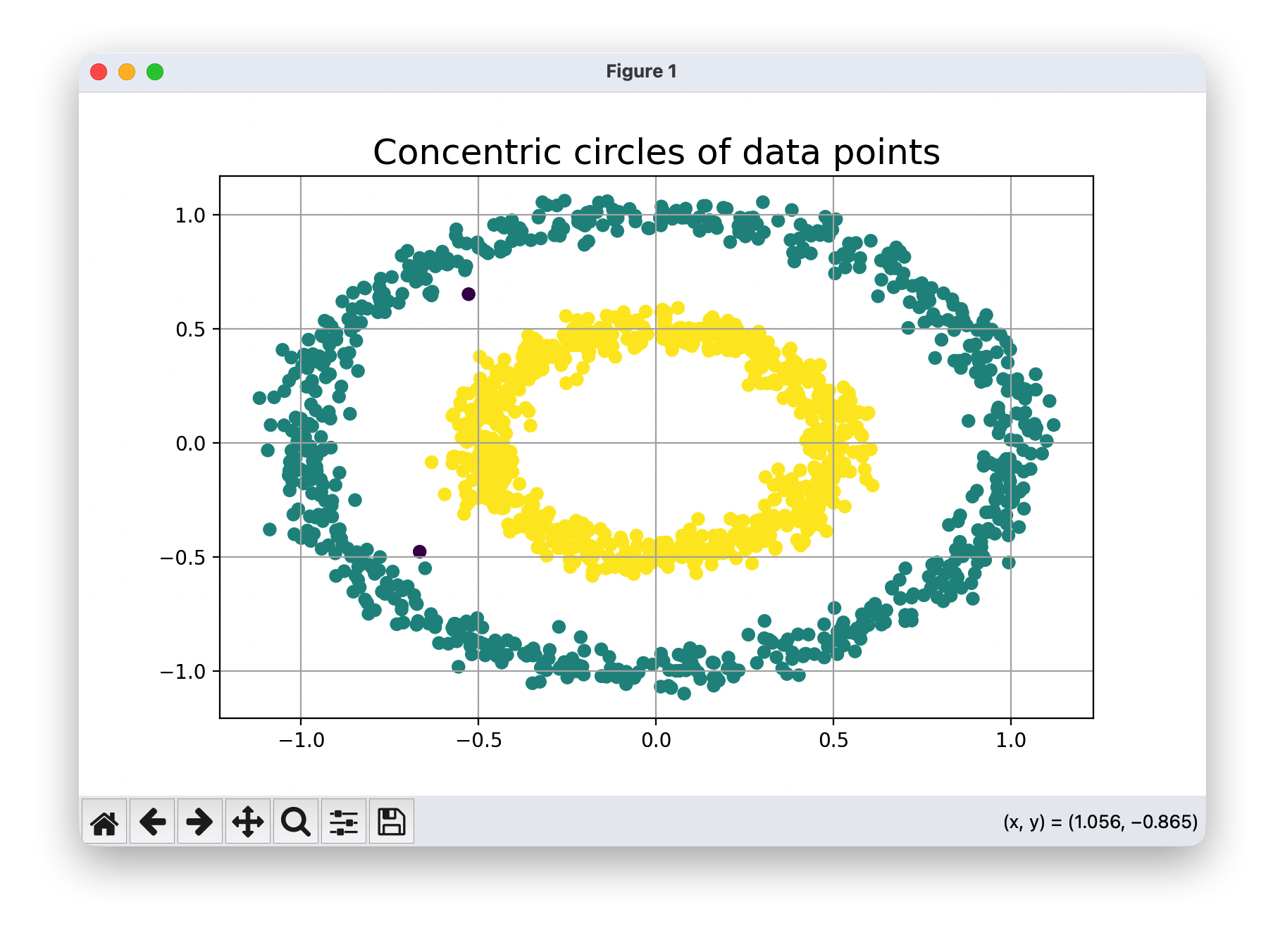
在这里插入图片描述

dbs.fit(noisy_circles)
plt.figure(figsize=(8,5))
plt.title("Concentric circles of data points", fontsize=18)
plt.grid(True)
plt.scatter(noisy_circles[:,0],noisy_circles[:,1],c=dbs.labels_)
plt.show()

在这里插入图片描述
月亮形状数据

优点：DBSCAN 在处理月亮形状数据时表现出色。由于其基于密度的聚类方式，能够很好地识别出两个月牙形状的聚类，而不像 K - means 那样受到形状的限制。它可以根据数据点的密度分布，将两个月牙区域分别划分为不同的聚类，得到符合直观认知的结果。
局限性：eps参数的选择对聚类结果影响较大。如果eps设置过小，可能会导致一些原本属于同一聚类的数据点被划分为噪声点；如果eps设置过大，可能会将不同的聚类合并成一个。

甜甜圈形状数据

优点：对于甜甜圈形状的数据，DBSCAN 同样能够较好地处理。它可以根据内外圆数据点的密度差异，将内圆和外圆分别划分为不同的聚类，而不是像 K - means 那样简单地按照距离划分。
局限性：同样，eps参数的选择至关重要。如果内外圆的密度差异较小，或者数据点的分布存在一定的噪声，可能会影响聚类的准确性。而且当数据集中存在不同密度的区域时，单一的eps值可能无法同时满足所有区域的聚类需求。