本文介绍了仙人掌图和圆方树的概念，包括它们的定义、构造方法和性质。通过圆方树，可以方便地解决仙人掌图上的最大独立集和最短路问题。文中给出了BZOJ4316、BZOJ1023和BZOJ2125等题目的解决方案，利用圆方树特性进行动态规划和最短路径计算。
1.什么是仙人掌
给你一张无向图，一条边最多只在一个简单环当中的图被称之为仙人掌，例如：
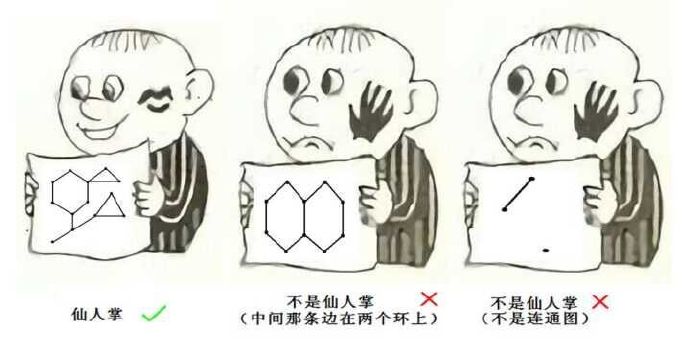
(图片源于网络)
2.什么是圆方树
仙人掌 G = ( V , E ) G = (V, E) G=(V,E) 的圆方树 T = ( V T , E T ) T = (V_T,E_T) T=(VT,ET) 为满足以下条件的无向图：
- V T = R T ⋃ S T , R T = V , R T ⋂ S T ≠ ∅ V_T = R_T \bigcup S_T, R_T = V , R_T \bigcap S_T \ne ∅ VT=RT⋃ST,RT=V,RT⋂ST̸=∅ , 我们称 R T R_T RT 集合为圆点, S T S_T ST 集合为方点
- ∀ e ∈ E \large{\forall} {e} \large\in E ∀e∈E , 若 e e e 不在任何简单环中, 则 e ∈ E T e \large\in E_T e∈ET
- 对于每个仙人掌的简单环 R R R ,存在方点 P R ∈ S T P_R \large\in S_T PR∈ST , 并且 ∀ p ∈ R \large{\forall} {p} \large\in R ∀p∈R 满足 ( P R , P ) ∈ E T (P_R, P) \large\in E_T (PR,P)∈ET , 即对每个环建立一个方点并连向这个环里的所有点
通俗一点的说 : 就是对于每个简单环都额外建一个方点 , 然后将每个圆点向方点连一条边 , 最后再将不连通的圆点连上原本有的边 , 就构成了圆方树
以下是对于圆方树正确性的证明：
感性证明
- 不在环上的点和边不会改变其树的性质, 而每个在环上的点都会连向方点, 形成一个菊花图, 所以这一定是一颗树
理论证明
- 原图中的环的个数为 ∣ E ∣ − ∣ V ∣ + 1 |E| - |V| + 1 ∣E∣−∣V∣+1 , 则 ∣ V T ∣ = ∣ S T ∣ + ∣ R T ∣ = ∣ V ∣ + ∣ E ∣ − ∣ V ∣ + 1 = ∣ E ∣ + 1 , ∣ E T ∣ = ∣ E ∣ |V_T| = |S_T| + |R_T| = |V| + |E| - |V| + 1 = |E| + 1, |E_T| = |E| ∣VT∣=∣ST∣+∣RT∣=∣V∣+∣E∣−∣V∣+1=∣E∣+1,∣ET∣=∣E∣ (大小为 r \textbf{r} r的环在仙人掌和圆方树中都是 r \textbf{r} r条边) , 因此满足 ∣ V T ∣ = ∣ E T ∣ + 1 |V_T| = |E_T| + 1 ∣VT∣=∣ET∣+1
3.如何构造圆方树
我们直接从任意一个点开始进行 T a r j a n Tarjan Tarjan 求点双联通分量 , 然后对于每一个点双联通分量建立一个方点 , 然后连边向这个点双联通分量里的每一个点连边, 最后处理没有连边的圆圆点对
P S PS PS : 个人建议通过并查集维护一下连通性在判断是否需要将原图中的边加入进来 , 而且这样可以避免重边带来的一些奇奇怪怪的 b u g bug bug
如图 :
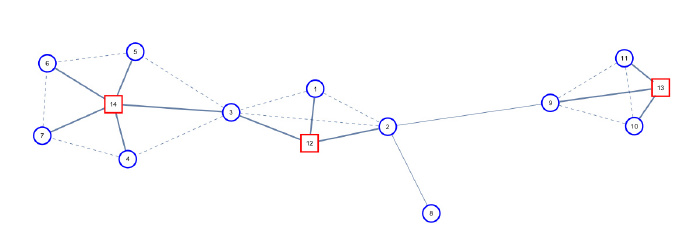
虚边是原图上的边 , 实边是新建立的圆方树上的边 , 有一些虚边和实边重和的请况可以按照上述并查集的方法来维护
4.圆方树的性质
- ∀ ( x , y ) ∈ E T , { x , y } ∩ R T ≠ ∅ \large{\forall} {(x, y)} \large\in E_T, \{x, y\} \large\cap R_T \ne \varnothing ∀(x,y)∈ET,{x,y}∩RT̸=∅ , 通俗点说就是两个方点一定不会相连
- 在构造的过程中无论取什么点为根 , 构造出的圆方树都是一样的(在形态上) , 因此圆方树是无根树
定义 : 子仙人掌
以 r \textbf{r} r为根的仙人掌上的点 p \textbf{p} p的子仙人掌是从仙人掌中去掉 p \textbf{p} p到 r \textbf{r} r的简单路径上的所有边之后 , p \textbf{p} p所在的联通块
- 以 r \textbf{r} r为根的仙人掌中 , 点 p \textbf{p} p的子仙人掌就是圆方树以 r \textbf{r} r为根时点 p \textbf{p} p的子树中的所有圆点所构成的图
5.利用圆方树和仙人掌解决问题
BZOJ4316小C的独立集
题面 : 求一颗仙人掌上的最大独立集
题解 : 我们先考虑如果在一棵树上应该怎么做 , 考虑状态
f
[
i
]
[
0
/
1
]
f[i][0/1]
f[i][0/1]表示这个点选或不选时以这个点为根的子树中的最大独立集是多少 , 那么转移就是 :
f
[
i
]
[
0
]
=
∑
v
∈
s
o
n
[
i
]
v
m
a
x
(
f
[
v
]
[
0
]
,
f
[
v
]
[
1
]
)
f
[
i
]
[
1
]
=
∑
v
∈
s
o
n
[
i
]
v
f
[
v
]
[
0
]
f[i][0] = \sum_{v \in son[i]}^{v} max(f[v][0], f[v][1]) \\ f[i][1] = \sum_{v \in son[i]}^{v} f[v][0]
f[i][0]=v∈son[i]∑vmax(f[v][0],f[v][1])f[i][1]=v∈son[i]∑vf[v][0]
我们再考虑环上如何转移 , 我们把这个环上深度最小的点称作这个环的根 , 我们还是考虑这个环的根选还是不选 , 然后我们把环展开 , 如果选择根节点的话 , 它两侧的点都是不能选的 , 否则就无所谓 , 然后剩下的就按树上的做法来搞就好了 , 所以转移就是 :
g
[
i
]
[
0
]
=
m
a
x
(
g
[
i
−
1
]
[
0
]
,
g
[
i
−
1
]
[
1
]
)
+
f
[
i
d
[
i
]
]
[
0
]
g
[
i
]
[
1
]
=
g
[
i
−
1
]
[
0
]
+
f
[
i
d
[
i
]
]
[
1
]
g[i][0] = max(g[i - 1][0], g[i - 1][1]) + f[id[i]][0] \\ g[i][1] = g[i - 1][0] + f[id[i]][1]
g[i][0]=max(g[i−1][0],g[i−1][1])+f[id[i]][0]g[i][1]=g[i−1][0]+f[id[i]][1]
最后的答案就是 m a x ( f [ r o o t ] [ 0 ] , f [ r o o t ] [ 1 ] ) max(f[root][0], f[root][1]) max(f[root][0],f[root][1]) , 这道题就这么愉悦的水过辣
BZOJ1023cactus仙人掌图
题目大意 : 给你一颗仙人掌 , 求仙人掌上的两点之间最短路的最大值 , 就是仙人掌的直径
题解 : 我们先考虑在树上怎么做 , 我们考虑状态
f
[
i
]
f[i]
f[i]表示在以这个点为根的子树当中, 经过
i
i
i这个点的最长链的长度, 转移很显然, 就是:
f
[
i
]
=
m
a
x
{
f
[
v
]
+
w
i
,
v
,
v
∈
s
o
n
[
i
]
}
f[i] = max \{ f[v] + w_{i,v}, v \in son[i] \}
f[i]=max{f[v]+wi,v,v∈son[i]}
然后我们就在转移的过程中更新一下答案就好了
然后还是一样的思路我们把环单独拎出来搞一下, 但是怎么弄呢, 发现不好在环上直接
d
p
dp
dp, 因为环上的最短距离是不确定的, 我们考虑把环拆成链, 直接在链上
d
p
dp
dp, 但是如果直接转移的话是
n
2
n^2
n2的, 式子是这样的:
a
n
s
=
m
a
x
(
a
n
s
,
m
a
x
{
f
[
r
]
+
f
[
l
]
+
r
−
l
,
r
−
l
<
l
e
n
2
}
)
ans = max(ans, max \{ f[r] + f[l] + r - l, r - l < \frac{len}{2} \} )
ans=max(ans,max{f[r]+f[l]+r−l,r−l<2len})
然后我们观察发现如果固定左端点, 新加入一个右端点我们可以将一些没有当前优的右端点给弹掉, 这个东西是可以用单调队列
O
(
n
)
O(n)
O(n)维护的, 具体的 :
- 如果当前队尾和队头的插值超过环的长度的二分之一, 弹掉队头, 直到符合条件为止
- 如果 f [ q [ t a i l ] ] + q [ t a i l ] ≤ f [ i ] + i f[q[tail]] + q[tail] \leq f[i] + i f[q[tail]]+q[tail]≤f[i]+i, 弹掉队尾, 直到符合条件为止
然后就可以开心的 d p dp dp辣
BZOJ2125最短路
题目大意 : 给你一颗仙人掌, 有 n n n次询问, 每次询问两点之间的最短路, n ≤ 1 0 5 n \leq 10^5 n≤105
题解 : 对于上面的题, 我们可以不用建圆方树, 但是这道题我们考虑将圆方树建出来, 但是有一个问题, 我们怎么设定圆点到方点的边权, 这里有一个小技巧, 我们对于每一个环都建立一个根, 每个圆点到方点的边权就是这个圆点在其所在的环中到这个环的根的最短距离, 这样的话就可以保证从深度小的点向深度大的点遍历时, 是点与点之间的最短距离
建完图以后, 对其进行倍增预处理, 和剖分, 对于每次查询 ( u , v ) (u, v) (u,v), 我们我们求一下 L C A ( u , v ) LCA(u, v) LCA(u,v) 如果 L C A ( u , v ) LCA(u, v) LCA(u,v)是圆点那么就和普通的树上查询距离是一样的答案就是 d i s [ u ] + d i s [ v ] − d i s [ L C A ( u , v ) ] dis[u] + dis[v] - dis[LCA(u, v)] dis[u]+dis[v]−dis[LCA(u,v)], 如果是方点的话, 就说明 u , v u, v u,v的祖先是在一个环上的, 这种情况不能直接搞, 我们用倍增向上跳到方点下的那个两个点 f a u , f a v fa_u, fa_v fau,fav, 让后求一下环上两点的最短距离 L L L,那么最后的答案就是 d i s [ u ] + d i s [ v ] − d i s [ f a u ] − d i s [ f a v ] + L dis[u] + dis[v] - dis[fa_u] - dis[fa_v] + L dis[u]+dis[v]−dis[fau]−dis[fav]+L
6.广义仙人掌
填坑中…
7.Summary
水水水
咕咕咕
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
