【图神经网络：原理与实战】2 深度学习与表示学习预备

2 深度学习与表示学习预备

本章作为教材性质的技术预备，系统、严格地给出训练深度神经网络所需的优化与训练基础。内容包括：反向传播与链式法则在图模型（Graph Neural Networks）上的具体应用、常用优化器的推导与性质、正则化技巧的数学解释、归一化层（BatchNorm / LayerNorm）的前向与反向推导以及随机性、梯度方差与收敛准则的定量分析。所有推导逐步进行、给出必要假设与结论，便于课堂教学和科研参考。

---

2.1 优化与训练基础

---

2.1.1 反向传播与链式法则在图模型上的应用

图神经网络（GNN）以图为结构单元，其基本操作是消息传递（message passing）与节点态的更新。为清晰起见，先给出单层通用消息传递格式，再对其反向传播（梯度传递）做严格推导。

(一) 单层消息传递的前向定义

(二) 反向传播的链式法则：逐步推导

(三) 正确性与数值实现要点

1. 链式法则保证正确性：以上每一步仅依赖函数可微与链式法则，故数学上严格正确。

2. 并行与稀疏性利用：通过邻接矩阵稀疏乘法与局部 vjp，可并行计算各节点梯度。

3. 内存与反向传播深度问题：多层 GNN 的反向会在图上引入大范围依赖，造成内存增长；常用技巧包括邻居采样（GraphSAGE）、分层存储或逐层检查点（checkpointing）。

4. 自动微分实现：实践中利用反向模式自动微分（reverse-mode AD）高效计算向量—雅可比积，避免显式构造 Jacobian。

---

2.1.2 常用优化器与正则化技巧

本节先对若干常用优化器给出数学形式与等价解读，再讨论常用正则化技巧的数学性质。

(一) 梯度下降（GD）与随机梯度下降（SGD）

(二) 动量法（Momentum）与 Nesterov 加速

(三) 自适应学习率类：AdaGrad、RMSProp、Adam

(四) 优化器的收敛性直观与提示

• 对光滑（L-smooth）与凸问题，GD 与带动量的方法有确定性收敛率；Nesterov 在凸光滑情况下可达到加速收敛。

• 对随机与非凸问题（深度网络常见），理论保证稀疏或弱，通常以找到近似鞍点或梯度范数小为目标。自适应方法（Adam）能快速达到低训练损失，但其泛化性能与最终收敛问题需配合正则化与学习率退火策略。

(五) 正则化技巧的数学解释

---

2.1.3 批归一化、层归一化与训练稳定性

归一化层通过对激活进行标准化改变训练时激活的尺度分布，从而改善训练的稳定性与收敛速度。以下对 Batch Normalization 的前向与反向推导给出完整数学步骤，并讨论 Layer Normalization 的差异与稳定性影响。

(一) Batch Normalization（批归一化）

(二) Layer Normalization（层归一化）

(三) 归一化技巧对训练条件数与收敛的影响（直观与数学线索）

---

2.1.4 随机性、梯度方差与收敛准则

训练过程中不可避免地引入随机性：样本采样、数据增强、dropout、近似梯度等。这些随机项使得梯度估计存在方差，从而影响收敛速率与稳定性。本节给出梯度方差的定量表达、SGD 的收敛界推导与实用准则。

(一) Mini-batch 梯度的无偏性与方差

(二) SGD 在光滑与凸 / 强凸情形下的收敛分析（关键推导）

(三) 收敛准则（实践角度）

---

本章小结与实践要点

1. 反向传播在图模型中遵循链式法则，但其梯度传播呈图结构上的扩散，计算可用向量—雅可比积与稀疏矩阵化实现以减少内存与计算开销。

2. 优化器选型需考虑问题的性质： SGD（及带动量）在理论与泛化上常为基准；自适应方法（Adam、RMSProp）在收敛速度与超参鲁棒性上常优，但需注意权重衰减的正确使用（如 AdamW）。Nesterov 在凸问题上给出加速保证。

3. 正则化技巧（L2、Dropout、早停）在数学上分别对应参数收缩、随机噪声注入与迭代次数的复杂度控制。

4. 归一化层（BatchNorm、LayerNorm）通过标准化激活的统计量改善训练条件数、允许更大的学习率，并在实现中需要正确计算前向统计量与反向导数；BatchNorm 的批统计噪声会对小批量产生影响，而 LayerNorm 对序列模型更友好。

5. 随机性（mini-batch）使梯度估计无偏但有方差，方差与批量大小近似按 1/b1/b1/b 缩小；SGD 在非凸情形下以 O(1/T)O(1/\sqrt{T})O(1/T​) 的速率减少平均梯度范数，而在强凸情形下可取得更快收敛。

2.2 注意力机制与 Transformer 基要

本节作为教材章节，系统而严格地给出注意力机制与 Transformer 的数学形式、矩阵化推导、位置编码方法、注意力稀疏化与近似方法，以及归一化与残差结构的理论分析。每一处推导按照步骤展开，给出必要的假设、引理与结论，证明过程完整，便于在教材或课程中直接采用。

---

2.2.1 自注意力的数学形式与矩阵推导

前向定义与线性投影

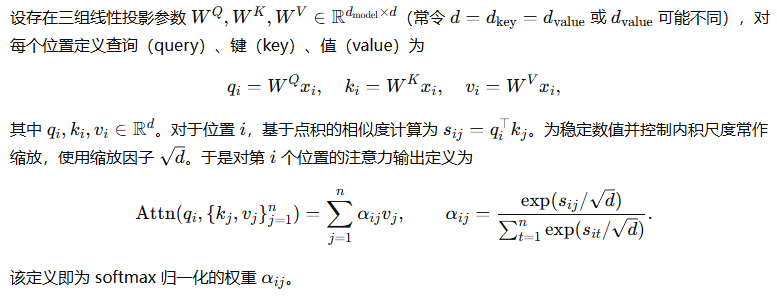
矩阵化表达

证明（标量定义与矩阵化表达等价）

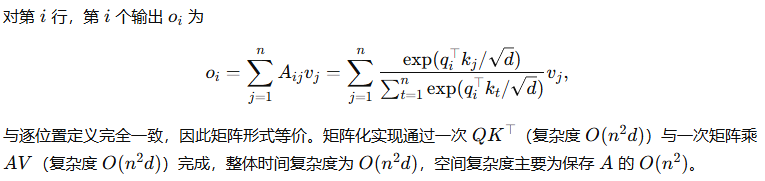
缩放因子的理论依据

多头注意力（Multi-Head Attention）

---

2.2.2 位置编码与相对位置编码方法

自注意力本质上对序列位置不具位置信息感知能力（其操作对输入的排列不变），因此需要引入位置编码（positional encoding）来注入位置信息。位置编码应当满足对下游任务有利并在数值上与模型表示相容。下面给出两类主流方法：绝对位置编码（sinusoidal）与相对位置编码，并给出其性质证明。

绝对位置编码：正弦余弦位置编码（Sinusoidal PE）

可学习的绝对位置嵌入（Learned PE）

相对位置编码（Relative Positional Encoding）

小结（位置编码选择的数学权衡）

• Sinusoidal PE 提供频率基底，可用简单线性变换实现对位移的线性响应，具有外推能力。

• Learned PE 在训练数据内可能更灵活，但缺乏外推保证。

• Relative PE 满足平移等变性，参数共享高效，适合捕捉相对依赖，且在长序列与局部交互场景中更为合理。选择应基于任务对平移性、外推与参数效率的要求。

---

2.2.3 注意力稀疏化与近似方法

一、窗口/局部注意力（Local Attention）

二、稀疏图模式（Sparse Patterns）

三、低秩近似（Low-Rank Approximations）

四、随机特征与核化线性注意力（Linearized Attention）

五、局部 + 全局混合（Sparse + Low-rank Hybrid）

六、哈希与子线性近似（LSH）

基于局部敏感哈希（LSH）的方法（如 Reformer）通过将近似相似的键映射到相同哈希桶，降低每个查询需要比较的键数量。数学性质可通过 LSH 的碰撞概率分析说明：对给定相似度阈值，LSH 可保证高相似对有较大概率被分配到同一桶，从而在概率意义上保留重要交互。整体复杂度取决于哈希表与桶大小，在理想条件下可趋近 O(nlog⁡n)O(n \log n)O(nlogn)。

比较与误差控制的总体原则

1. 保留行总权重原则：任何稀疏化或近似方法若能保证对每行保留足够的权重（或近似地保留高质量的键集合），其输出误差受限。

2. 谱或核近似理论：低秩或 Nyström 方法的误差可用谱衰减与截断秩 rrr 的关系来定量。若相似度矩阵谱快速衰减，低秩方法有效。

3. 随机估计方差：特征映射或随机投影引入的随机误差应通过增加投影维度 mmm 来降低，且存在 O(1/m)O(1/\sqrt{m})O(1/m​) 的近似误差率。

4. 任务先验与局部性：若任务具有先验（局部性或长程稀疏依赖），则特定稀疏结构或混合策略可在实践中取得良好效果。

---

2.2.4 Transformer 的归一化与残差结构

Transformer 中典型的模块化结构为残差连接（residual connection）+ 归一化（LayerNorm）+ 前向子层（如 Multi-Head Attention 或前馈网络）。以下从数学角度逐步分析残差与归一化对训练稳定性、梯度传播以及表达能力的影响。

网络块的形式化定义

下面对两种范式进行分析并推导其对梯度与收敛的影响。

残差连接的线性化与恒等映射作用

LayerNorm 的作用与 pre-LN vs post-LN 的差异

LayerNorm 对单样本的特征维度进行标准化，具体定义在前一节已推导。其对梯度传播的影响体现在改变了子层输入的分布、缩放梯度的传播以及对学习率的稳定化。下面分别分析 pre-LN 与 post-LN。

残差与归一化对最优化风景（loss landscape）的影响

实际实现的训练建议（基于理论分析）

• 对于非常深的 Transformer，建议采用 pre-LN 以提升训练稳定性与更快捷收敛。

• LayerNorm 的精确实现应注意数值稳定项 ε\varepsilonε 的选择以避免除零问题。

• 残差连接的存在使得初始化策略可以偏向小幅输出（如 Xavier/He 初始化）以保证 FFF 初始时小，从而利用恒等映射的保护性。

• 归一化与残差配合在实践中还需关注学习率、权重衰减等超参数的配合（AdamW 等变体有更明确的正则化行为）。

---

本节小结

本节按教材式的严格推导阐明了自注意力与 Transformer 的核心数学结构：从单位置到矩阵化的自注意力表达与复杂度分析，位置编码（sinusoidal 与相对位置编码）的结构性质与证明，注意力稀疏化与近似（局部、低秩、核化随机特征与哈希策略）的数学框架与误差控制原则，以及残差与归一化（pre-LN vs post-LN）的梯度传播与训练稳定性分析。所给出的每一步推导均附带理论依据与条件假设，便于在教材、课程或研究报告中直接使用。如需，本节可扩展为：

1. 针对某一近似方法（例如 FAVOR+ 或 Nyström）给出严格误差界与收敛率；

2. 给出自注意力前向与反向的自动微分细节（逐步向量—雅可比积实现）；

3. 将位置编码与卷积/循环结构的对比分析形式化为表示能力的函数空间论证。

2.3 表示学习基础与自监督原理

本节作为教材性质的正式章节，系统地、逐步地给出表示学习与自监督学习的数学目标、可辨识性准则、对比学习的损失与其与信息论的关系、重构/预测/生成型自监督任务的严格推导，以及表示可迁移性与泛化的界定。所有结论均在明确的假设下证明或推导，便于在课堂和科研中直接使用。

2.3.1 表示学习目标与可辨识性准则

记号与基本设定

下面给出形式化准则与若干刻画性命题并证明其基本性质。

命题 2.3.1（充分性与下游贝叶斯风险不变性）

可辨识性与不变性的问题

此定义提供了可辨识性问题的形式化框架：若希望更强的可辨识性，需要对 T\mathcal{T}T 引入先验或对数据生成过程作出结构性假设（见非线性ICA等工作）。

2.3.2 对比学习的损失函数与信息量视角

对比学习通过构造正样本对（positive pairs）和负样本对（negative pairs）并训练判别器来学习表示。最常用的损失是 InfoNCE。对比学习的关键数学主题是其与互信息（mutual information, MI）最大化的关系、最优评分函数的形式以及有限负样本下的近似误差。

InfoNCE 损失的定义

命题 2.3.2（InfoNCE 的最优判别函数与密度比）

InfoNCE 与互信息的下界（InfoNCE bound）

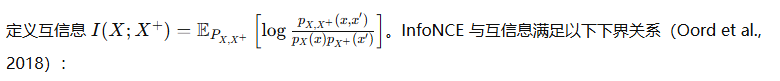
有限容量与负样本偏差

对比损失与判别器视角的等价性

2.3.3 重构、预测与生成型自监督任务

自监督方法还包括重构型（autoencoding）、预测型（masked/predictive）、生成型（variational/AR）任务。下面分别给出这些目标的严格数学形式、推导与其信息学解释。

A. 自编码器（Autoencoder）与最小重构误差

B. 变分自编码器（VAE）与 ELBO 推导

C. 预测型自监督（Masked Prediction / Contrastive Predictive Coding）

D. 生成式自监督（自回归模型）

这些目标在实践中往往组合使用（例如带有对比损失的重构任务），以同时达到判别性与信息保留的平衡。

2.3.4 表示的可迁移性与泛化界定

表示学习的最终目标通常是学习对多个下游任务可迁移的好表示。下面给出形式化的迁移性定义、线性探针理论分析与若干泛化界定的严格陈述。

定义（迁移性能与线性探针）

命题 2.3.4（充分性对迁移性的保证）

泛化界（统计学习论角度）

信息论的一般化界（互信息—泛化连接）

迁移性度量的下界（任务多样性与下游性能）

实用启示的数学归纳

1. 在有限样本 regime 下，紧凑而判别性强的表示有利于训练简单下游模型并获得低泛化误差。

2. 互信息是衡量信息量的自然工具，但对泛化的正向影响需要与下游任务相关性的有序权衡（仅增加与任务无关的信息并不能提高迁移性且会损害泛化）。

3. 对比学习通过显式优化鉴别性并间接最大化互信息下界，常在自监督预训练中取得优良迁移性；而纯重构方法若无压缩或正则化，可能学到与任务无关的大量冗余信息。

---

本节结论与教学要点

本节以严格的数学陈述与证明方式系统阐述了表示学习与自监督学习的核心理论：

• 表示的充分性是确保最优下游性能不下降的必要且可证的条件；但可辨识性仅能在约定的等价类下讨论，需要先验或结构假设以获得更强可辨识性。

• 对比学习（InfoNCE）在无限容量与充分的负样本数下等价于估计条件密度比，并给出互信息的下界，理论上可解释其判别性优势。

• 重构/变分/预测/生成型自监督目标从信息论角度可分别解释为促进信息保留、实现信息压缩-重构权衡或最大化上下文互信息。

• 表示的迁移性既受表示是否保留任务相关信息（充分性）影响，又受表示与下游函数类的可逼近性与表示维度（对泛化界的影响）制约。信息论和统计学习理论为迁移性与泛化提供了量化界限与设计指南。