【图神经网络：原理与实战】3 消息传递框架（MPNN）

3 消息传递框架（MPNN）

本章严格而完整地给出消息传递神经网络（Message Passing Neural Networks, MPNN）的泛化形式、核心算子（消息、聚合、更新、读出）的形式化定义、空间域与谱域卷积的等价性推导，以及消息传递的稳定性与信息衰减（over-smoothing）分析。每一步均列出必要假设并做出严格推导，适合作为教材中算法原理章节的正式内容。

3.1 泛化形式与统一表达

3.1.1 消息与聚合函数的形式化定义

3.1.2 更新、读出与全局表示映射

3.1.3 空间域与谱域的等价关系推导

图上的卷积/滤波可从两个视角构造：空间域（基于邻居聚合的局部操作）与谱域（基于图拉普拉斯的特征分解的频域滤波）。下面推导在一定条件下两者的等价和近似关系，并给出常用的多项式近似与实践化简（例如 GCN 的一阶近似）。

谱域定义及谱卷积

多项式近似与空间实现

GCN 的一阶约化（Kipf & Welling）推导示例

空间-谱等价性的结论性陈述

在可解释性条件下（滤波器平滑、谱函数可多项式近似、图大小与谱分布合理），空间域基于邻域聚合的 MPNN 与谱域多项式滤波在表达上等价或近似等价。该等价性为将频域设计的滤波器移植为可并行、稀疏的局部消息传递结构提供了理论依据。

3.1.4 消息传递的稳定性与信息衰减分析

消息传递层重复应用会引发两个重要现象：一是对图结构或输入扰动的稳定性问题；二是层数增加时表示趋向退化（所谓 over-smoothing 或信息衰减）。本节从算子谱与 Lipschitz 常数出发，给出严格界和证明。

模型化设定与假设

稳定性：对输入扰动与图扰动的敏感性

小结

3.2 经典变体与结构差异

本节系统而严格地推导图神经网络若干经典变体的数学原理：GCN 的谱视角与离散化推导、GraphSAGE 的邻居采样与聚合函数的统计性质、GAT 的注意力机制与权重归一化推导、GIN 的表达力与与 Weisfeiler–Lehman（WL）等价性的严格论证。每一小节按步骤展开推导并给出必要引理与证明，保持逻辑闭合与数学严谨，可直接作为教材中算法原理章节内容。

3.2.1 GCN 的谱视角与离散化推导

第一步：用多项式逼近实现局部滤波

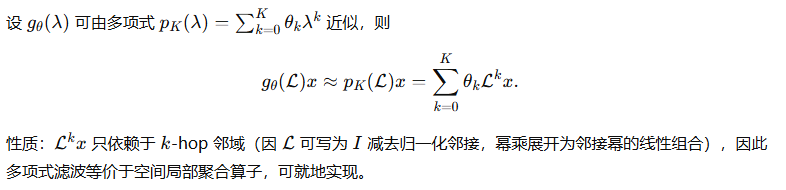
第二步：Chebyshev 展开（数值稳定的多项式近似）

第三步：一阶近似与 GCN 的离散化

第四步：数值稳定性与自环的必要性

结论（GCN 为谱滤波的低阶离散化）

由以上步骤得到：GCN 的更新形式是对谱域图滤波器以低阶多项式近似并在空间上离散实现的结果。该推导在假设滤波器光滑且可由低阶多项式逼近时成立。谱视角为 GCN 的设计（归一化、加自环、共享权重）提供了理论依据，并解释了其局部性与有效性。

3.2.2 GraphSAGE 的邻居采样与聚合函数

GraphSAGE（Hamilton et al.）提出将聚合器设计与邻居采样相结合以便扩展到大图与 inductive 场景。下面严格说明采样—聚合的数学机制，并推导采样估计的无偏性与方差界。

算法性描述（形式化）

无偏性：采样均值估计

方差界（简单独立抽样近似）

采样对计算复杂度的影响

聚合函数的设计与表达力

Mean aggregator：等价于对邻居特征做线性平均，简单且稳定，但对多重集合的区分能力有限。
Pool aggregator（max/mean + MLP）：先对每个邻居经过共享 MLP，再做非线性池化（max/mean），能提高对局部异质结构的表达能力。
LSTM aggregator：将邻居按某顺序输入 RNN 并取隐藏态，理论上能表达序列性的组合，但因序列顺序不确定而依赖网络学习的鲁棒性。

统计误差对下游表示的影响

3.2.3 GAT 的注意力机制与权重归一化

GAT（Graph Attention Network）把注意力机制引入邻居加权聚合，从而得到可学习且自适应的邻居权重。下面对 GAT 的注意力系数定义、归一化形式、置换不变性及等价到加权邻接的证明性说明做严格推导。

算子形式定义

置换不变性与局部化

归一化的数学角色

等价性到加权邻接的解释

可微性与梯度形式（要点）

多头注意力的稳定化与表示能力

多头通过在不同线性子空间上并行计算注意力并合并，等价于对输入空间做多重自适应加权与特征变换，使模型有能力在不同子空间上关注不同邻居关系。数学上，多头的拼接给出更高维的表示，从而提高判别能力与鲁棒性。

3.2.4 GIN 的表达力与 WL 等价性分析

Graph Isomorphism Network（GIN）设计目标是使 GNN 在判别图结构上尽可能接近 Weisfeiler–Lehman（1-WL）图同构测试的判别能力。下面给出 GIN 的更新形式，并证明在合适条件下 GIN 的表示对多重集合的区分力与 1-WL 等价。

GIN 的更新公式

要求与关键性质：对多重集合的注入性

主定理（GIN 对 1-WL 的判别下界与等价性）

细节说明：为什么需要可学习 ϵ\epsilonϵ

GIN 的表示力与实践含义

结论：在合理假设下（节点特征离散或 MLP 足够强），GIN 把 GNN 的表达力提升到了 1-WL 的上界。此结论解释了为何在许多图判别任务中 GIN 比较浅显的 mean/pool 聚合方法更具判别力，但也说明了任何一阶邻域聚合模型的本质上限：若任务需要超越 1-WL 等价类的判别能力（例如需要识别更高阶的子图结构），则需要引入更强的结构（higher-order WL，subgraph-aware features，or random features 等）。

小结

GCN：从谱滤波出发经 Chebyshev 多项式逼近并在空间上离散化得到的第一阶近似，解释了 GCN 的归一化、共享权重和自环设计原则。谱视角明确了滤波的局部性与近似误差来源。
GraphSAGE：通过邻居采样与多种聚合器（mean/pool/LSTM）实现可扩展的 inductive 学习；采样估计具有无偏性、方差随采样数 KKK 递减；设计取舍在计算复杂度与统计估计误差之间。
GAT：利用可学习的点积式注意力并以 softmax 做局部归一化，得到自适应的加权邻接矩阵；注意力的竞争性及多头机制提升表达力与鲁棒性。
GIN：通过 sum 聚合结合 MLP 构造注入式多重集合映射，使得网络判别能力达到 1-WL 的上界；理论证明了其在判别图同构测试上的最强一阶能力及设计动机（引入 ϵ\epsilonϵ 保证注入性）。

3.3 表达力、可辨别性与限制

本节以严格的数学语言系统论述图神经网络（GNN）的表达力限制与扩展策略：首先从 Weisfeiler–Lehman（1-WL）测试出发给出等价性与判别下界；继而讨论通过高阶子图与子结构编码扩展表达力的原则与构造；接着用谱与算子论方法给出过平滑（over-smoothing）的精确刻画与界；最后从雅可比谱与链式法则出发分析深层 GNN 的可训练性与梯度流失/爆炸问题。每一命题均给出必要假设、逐步推导与证明要点，以教材章节的标准编排。

3.3.1 Weisfeiler–Lehman 等价性与判别下界

背景与记号

定义（GNN 与 1-WL 的可比性）

命题 3.3.1（任一基于多重集合聚合的、层次可表示为 sum/mean/max + 可逆映射的一阶邻域 GNN 不超越 1-WL）

命题 3.3.2（GIN 达到 1-WL 的上界） —（已在 3.2.4 证明大纲）

在适当的映射（注入 MLP）与 sum 聚合下，GIN 可以区分任意由 1-WL 区分的图；因此其表达力等于 1-WL。

含义：1-WL 给出了一阶消息传递类模型在图同构判别能力上的可证明上界；要超越此上界必须引入超越单纯邻域多重集合的信息（例如高阶子图、节点对关系、随机特征或子图化策略）。

3.3.2 可表达性扩展（高阶子图、子结构编码）

若任务需要区分 1-WL 难以区分的结构（例如某些对称非同构图），需采用更丰富的结构信息。常用扩展分为三类：高阶 WL（k-WL）与对应的高阶 GNN、子图/子结构编码（subgraph GNN）、以及引入随机/标志性特征（random features）。

高阶 Weisfeiler–Lehman（k-WL）与 k-GNN

子图与子结构编码（Subgraph GNN）

随机特征与节点标识（Random features / ID）

向节点注入随机或唯一标识（如随机向量、node id 的可学习编码）可以破坏对称性，从而使 GNN 在某些任务上突破 1-WL。理论上，当引入足够独立的随机特征（和恰当的训练机制）时，模型可以借助这些特征辨识更多结构，但泛化与可解释性问题需谨慎处理。

3.3.3 过平滑现象的数学刻画

过平滑指节点表示随着层数增加在图上趋向同一或低维子空间，导致判别能力下降。以下在更精确的算子语言下给出刻画与界。

线性化模型与谱分析的精确刻画

非线性与权重存在时的扩展

过平滑的速率量化（谱间隔视角）

抑制过平滑的数学对策

3.3.4 深层 GNN 的可训练性与梯度流失问题

深层网络面临梯度消失与爆炸问题。对 GNN，除了标准深度网络问题外，还叠加了图结构引入的算子谱影响。下面从雅可比与链式法则出发给出定量分析。

链式法则与梯度的谱乘积表示

GNN 特有因素

定量条件（可训练性的充分条件示意）

梯度传播与层内耦合的示例计算

3.4 改进策略与算法复杂度

本节给出用于改进 GNN 可训练性、抑制过平滑并控制资源消耗的若干策略的形式化描述与数学分析。内容包括跳连/残差连接的形式化与对梯度流的影响分析；正则化与归一化手段（包括 DropEdge 等图级随机正则化）的数学性质；详细的时间与空间复杂度分析；以及并行／分布式执行时的瓶颈建模与可行算法工程策略。所给推导要求明确假设、逐步展开，便于教材直接采用。

3.4.1 跳连（skip connection）与残差连接形式化

形式化定义与变体

残差对梯度流的影响（谱/雅可比证据）

引理 3.4.1（残差下的雅可比乘积上界与下界）

本引理给出残差帮助维持雅可比谱在数值上可控的数学依据，从而解释残差层在深层 GNN 中有助于保持梯度流的直观作用。

跳连拼接对表示维度与计算资源的影响

3.4.2 正则化与归一化手段（dropedge、批正则）

DropEdge：图边随机删除的形式化与分析

批正则与归一化（BatchNorm / LayerNorm / PairNorm 等）

BatchNorm / LayerNorm 在 GNN 中的作用

3.4.3 时间复杂度与空间复杂度分析

下面对常见 GNN 前向/反向单层操作给出精确的复杂度模型，并说明跳连、注意力与采样等变体对复杂度的影响。

基本操作与符号

记：

采用稀疏邻接矩阵乘法与稀疏存储为基准。

单层标准 GCN（归一化邻接 + 线性变换 + 非线性）

实现步骤典型为：

注意力类（GAT）

采样方法（GraphSAGE）

跳连/拼接对复杂度的影响

反向传播的复杂度

反向传播的时间复杂度与前向相同阶别，通常为前向的常数倍（约 2–3 倍），且需额外的内存用于保存中间激活。反向传播中涉及稀疏矩阵转置乘法，时间成本与稀疏密切相关。

3.4.4 并行化与分布式执行的瓶颈分析

在大规模图学习场景中，单机无法容纳全部图与激活，需并行化或分布式执行；下述分析抽象化通信、计算与同步成三个关键量，并量化瓶颈来源与消减策略。

并行模型与关键成本项

图划分策略与通信量

小批量与采样对通信的影响

采用邻居采样与微批训练（mini-batch）能显著降低单次通信量：每次仅需传输被采样子图内的跨分区边所需的节点特征。若每次采样的局部子图包含 sss 条跨分区边，则通信缩减为 O(sd)O(s d)O(sd)。因此在大规模图上，采样是降低通信瓶颈的首要工程手段。

模型并行 vs 数据并行

数据并行（数据 parallelism）：每个 worker 拷贝完整模型，处理不同数据分片（图批或子图）。通信在参数同步（梯度同步或参数服务器架构）上发生。通信量与模型大小（参数量）及同步频率有关。
模型并行（model parallelism）：把模型参数切分到不同 workers（常用于极宽或占内存大的模型）。通信在前向/反向过程中传递中间激活或梯度，开销与激活大小相关。GNN 通常优先采用数据并行（因模型相对小）或图划分与数据并行的混合策略。

通信—计算比（Communication-to-Compute Ratio）与扩展性界

延迟与同步对收敛的影响（概率性说明）

异步与延迟训练在实践中可减少同步成本，但引入“陈旧梯度”或“延迟参数”问题。若延迟上界为 τ\tauτ，理论结果（在 SGD 类优化的通用性陈述）表明：若步长恰当衰减，则对无约束凸目标的收敛率会退化为与 τ\tauτ 成正比的项；即延迟越大，收敛速率越慢或波动越大。实务上，延迟的有害影响与步长调度、数据非平稳性与梯度方差共同决定，需以工程策略折中。

工程实践中的缓解手段

最小化边割：使用高质量图划分工具以减少跨分区边数。
邻居采样/子图训练：通过采样降低每次通信量，并允许按 mini-batch 并行化。
特征压缩与量化：在传输特征时使用低精度（如 16-bit、8-bit）或梯度压缩（Top-k / quantization）减少带宽消耗，需注意数值稳定性。
通信-计算重叠（pipelining）：在等待传输时并行化本地计算，减少同步等待。
稀疏聚合缓存：对频繁访问的跨区节点做本地缓存并周期性同步以减少频繁通信，代价是精度上的轻微延迟（staleness）。
混合并行策略：对大规模节点采用图划分 + 每个 partition 内再做数据并行或模型并行，结合使用高效 RPC / RDMA 网络以降低延迟。