【图神经网络：原理与实战】第九章异构图神经网络-优快云博客

本章把“异构图”（heterogeneous graph）从数学上形式化，分析异构结构对表示学习与训练的影响，并给出用于工程实现的严格推导与可验证结论。第 9.1 节逐项定义异构图的基本构件：节点/边类型与元图（meta-graph）；随后定义并推导元路径、元图统计量与基于路径的语义嵌入的数学表达；讨论类型不平衡与稀疏性在消息传递与梯度上带来的定量效应，并给出对策；最后把常见任务（节点/关系/子图层面）用统一的数学形式写出，便于后续算法设计与评估。所有推导给出必要假设、步骤与结论，足够严谨可用于教材或论文的方法章节。

9.1 异构图的形式化定义

9.1.1 节点类型、边类型与元图表示

定义 9.1（异构图）
一个异构图（heterogeneous graph）是五元组

讨论/注释： 异构图的核心在于不仅节点特征不同，而且不同类型节点之间的连边在语义上常是不对称或多样的，例如在知识图谱中“作者—写作—论文”与“论文—发表—会议”属于不同边类型。为便于后续代数表达，我们常把异构图拆分为按类型索引的子集合与子图。

按类型分割的表示

9.1.2 元路径、元图统计量与语义嵌入

异构性最自然的表达是元路径（meta-path）与元图样式（metagraph pattern）。这些对象能把跨类型的语义路径编码为可计算矩阵运算。

9.1.3 类型不平衡与稀疏性问题刻画

异构图常出现的两个核心挑战是：不同类型节点/边数量极不平衡（type imbalance），以及某些类型之间连通性极为稀疏（sparsity）。下面以数学形式刻画这些现象，并推导它们对消息传递与梯度的影响。

量化不平衡与稀疏性指标

对消息聚合的影响（定量推导）

问题 1（偏差：多数类型主导）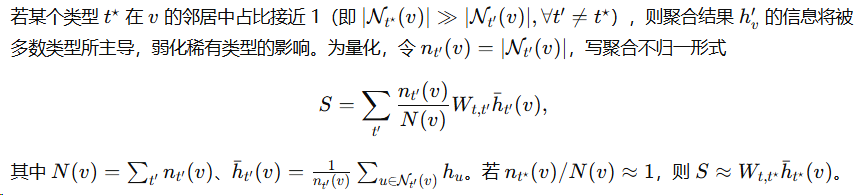

问题 2（方差：稀疏类型引入高方差估计）

结论（对训练的量化影响）
将多个类型的消息线性组合时：

主导类型提供稳定但可能偏倚的信息（bias），使模型难以学习稀有类型的特定信号；
稀疏类型在样本均值估计上噪声高（variance），导致参数更新波动，训练不稳定。

下面给出两个数学命题刻画这些影响并给出对策。

命题 9.2（消息幅度与类型度数的期望比例）

9.1.4 任务定义：节点/关系/子图层面的差异

异构图上的任务常比同构图更复杂，因应不同层面的问题要用不同的目标函数与评价指标。下面以统一符号形式把主要任务类型形式化，并指出异构性带来的特殊性。

1. 节点分类（Node classification，带类型）

2. 关系预测 / 边预测（Link / Relation prediction）

3. 子图/图模式预测（Subgraph / motif prediction）

4. 多任务与层次任务

小结

本小节把异构图从基础构件到任务层面做了完整、严密的数学形式化：

9.2 聚合与跨类型变换机制（正式章节）

本节从算子与代数的角度系统推导异构图神经网络中核心的聚合与跨类型变换机制。先在统一符号下给出类型条件化消息传递的一般形式，然后分别推导（1）类型特异性变换矩阵的设计与性质；（2）跨类型注意力与多头机制的数学表达与包含关系；（3）基于元路径的聚合算子与语义过滤器的构造与稳定性；（4）类型对齐与共享表示的分解与识别性。每一小节都以定义、命题、引理与证明展开，步骤严密，可直接作为算法原理章节使用。

9.2.1 类型特异性变换矩阵的设计

目标与出发点

基本构造与线性表述

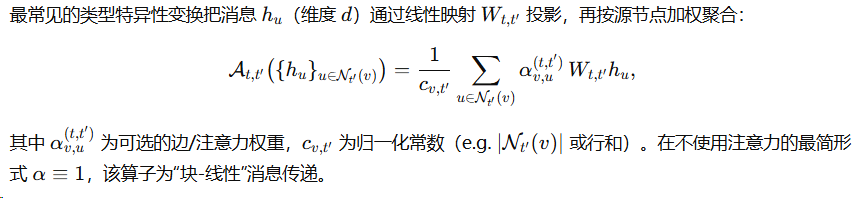
标准化与谱稳定性（必要性）

命题 9.2.1（谱约束保证多层稳定性）

参数共享与低秩近似（参数效率）

9.2.2 跨类型注意力与多头机制

跨类型注意力的一般形式

多头设计与容量分解

命题 9.2.3（多头注意力增加表达能力）

包含关系：注意力包含基于类型的线性聚合

数值稳定性与复杂度分析

9.2.3 元路径聚合与语义过滤器

元路径聚合算子构造

语义过滤器的引入与设计算法学理

定理 9.2.4（过滤器降低噪声的条件）

数值实现与计算注意

这些近似的方差与误差界可以按章节 8.3 中的采样与低秩误差模型进行量化。

9.2.4 类型对齐与共享表示策略

问题描述与核心思想

在异构图中，尽管不同类型节点本质上属于不同语义域，通常仍存在共享的跨类型语义（例如“作者”与“机构”都可用来解释某一话题）。因此设计既能保留类型特异性又能提取跨类型共享信息的表示结构是必要的。数学上把每个类型的表示视为由“共享子空间”与“类型特异子空间”两部分构成。

共享+特异分解模型

命题 9.2.5（方差分解与泛化论据）
把总体表示方差写为

类型对齐策略（映射/正交化）

若不同类型的原始特征位于不同度量空间，需要先做对齐映射。常见做法与数学理据如下。

定理 9.2.6（对齐约束改善下游任务泛化）（条件性陈述）

共享参数与迁移学习策略

完全共享：对所有类型使用同一映射/参数，参数数目最少但在类型差异大时会欠拟合特异性模式。
完全分离：每类型独立参数，灵活但参数量大且对稀有类型会过拟合。
混合共享（shared + private）：把层分解为共享基与类型特异基（如前）；数学上可证明这种分解在样本稀缺与类型共性存在时具有最优的偏差-方差权衡。

小结（章节结论与工程要点）

本节由浅入深地推导了异构图神经网络中四类核心机制的数学基础与实现要点：

每一项设计均给出可检验的数学条件（谱界、Lipschitz 常数、低秩近似秩、采样方差公式等），便于在实现时把理论保证转化为具体的正则化、约束与超参数选择。按本节推导构造的异构 GNN 算子，既能保证数值稳定性与可扩展性，也能在类型复杂性与数据匮乏的现实问题中保持良好的泛化性能。

9.3 异构自监督与对比策略

异构图中存在多种节点类型与边类型，使得其结构模式、语义依赖与统计特性远比同构图复杂。自监督学习在此类图上发挥关键作用：通过不依赖标注数据构建训练信号，使模型能够充分挖掘结构模式、类型依赖与语义一致性，实现高效的结构建模与知识迁移。由于异构图的多类型特性，自监督目标必须同时考虑局部结构、跨类型相关性与全局一致性，因此需要设计类型感知的视图构造机制、跨类型对比策略与多任务训练框架。本节从理论基础出发，系统构造异构自监督策略，并给出形式化推导。

9.3.1 类型感知视图构造方法

（1）结构保持的类型约束视图

（2）属性扰动与语义增强视图

9.3.2 跨类型正负样本定义与采样

异构对比学习的关键在于正负样本对的合理构造。由于节点类型不同，若直接将所有节点视为候选样本，会破坏语义一致性，因此必须定义类型一致的正样本与类型可控的负样本。

（1）同类型正样本对

（2）跨类型语义正样本对

（3）负样本策略

负样本需要满足类型控制和语义分离：

负样本构造严格保证信息区分度，提高对比信号质量。

9.3.3 多任务损失与协同训练框架

异构自监督需要融合结构一致性、语义约束与类型对齐，因此构建多任务损失函数：

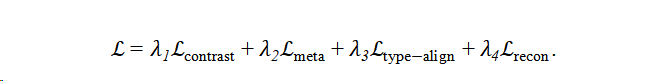
下面对各项做形式化推导并说明其训练与优化策略。

（1）跨视图对比损失

（2）元路径语义损失

该项建立异构语义一致性，从而把元路径语义直接注入表征学习。

（3）类型对齐损失

（4）重构损失

若模型含编码器-解码器，则对重构邻接张量施加约束：

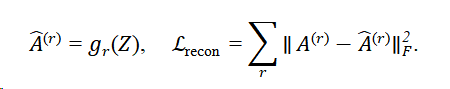
重构损失鼓励嵌入保留图的拓扑信息，类型条件化的解码器 grg_rgr 可增强捕捉异构语义的能力。

协同训练策略：因各项损失尺度不同，建议采用自适应权重策略（如动态权重平均）或先预训练对比与元路径项，再联合微调重构与对齐项，从而提升稳定性与下游迁移效果。

9.3.4 迁移学习与领域自适应案例

异构图的自监督学习具有天然迁移能力，可用于新类型、稀疏类别或不同结构分布的图。迁移学习过程包含两个核心机制：跨域对齐与结构语义保持。

（1）跨图类型对齐映射

源图和目标图分别为

（2）分布对齐损失

为解决分布偏移，引入基于嵌入均值或高阶统计的对齐损失，例如最大均值差（MMD）形式：

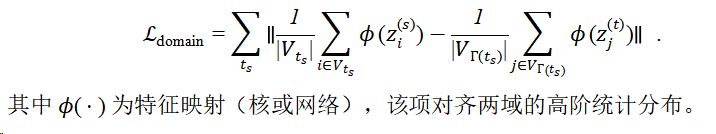
（3）跨域语义保持

若源域元路径语义在目标域仍成立，则要求

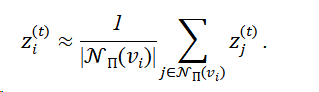
通过语义一致性约束阻止跨域退化并保持异构语义结构。

（4）迁移学习整体目标

最终迁移目标综合上述约束：

章节总结

本节系统构建了异构图自监督框架，涵盖视图构造、正负样本定义、多任务损失体系与迁移学习机制。关键思想包括：利用类型和元路径保持语义一致性；通过类型区分的对比学习提升特征判别性；通过多任务损失联合建模结构、语义与类型对齐；利用高阶统计匹配实现无标注迁移。若需要，可以进一步把上述理论落地为可执行的训练伪代码、实用的超参数建议与实验设计（包括视图生成概率、负样本比率、温度 τ\tauτ 的选择与动态权重策略），或继续撰写下一节关于“异构图的模型优化与稳定性分析”。

明白，我会把上一版内容去掉所有分割线，保持原来的章节、段落和推导结构不变，直接整理成正式章节风格：

9.4 行业应用与性能考量

在工业界和商业场景中，异构图神经网络（Heterogeneous Graph Neural Networks, HGNNs）由于其能够刻画节点和边的多样性以及复杂关系的能力，在知识图谱、推荐系统以及风控等领域表现出极大的潜力。然而，在实际应用中，性能优化和系统可扩展性是制约其广泛落地的关键因素。本节将从应用场景出发，详细推导各类异构图模型的核心原理，并分析其工程实现和性能考量。