代码随想录算法训练营第 6 天 | 454. 四数相加 II、383. 赎金信、15. 三数之和、18. 四数之和-优快云博客

454. 四数相加 II、

分组法，两两一组（思想有点想归并)，保证复杂度是 O(n^2)

用 map，value 保存的是出现的次数

class Solution {
    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        int n = nums1.length;
        HashMap<Integer, Integer> map = new HashMap<>();
        int cnt = 0;
        for (int i : nums1) {
            for (int j : nums2) {
                map.put(i + j, map.getOrDefault(i + j, 0) + 1);
            }
        }
        for (int i : nums3) {
            for (int j : nums4) {
                int target = - (i + j);
                if (map.containsKey(target)) {
                    cnt += map.get(target);
                }
            }
        }        
        return cnt;
    }
}

383. 赎金信

题目链接

哈希法，简单

class Solution {
    public boolean canConstruct(String ransomNote, String magazine) {
        int n1 = ransomNote.length();
        int n2 = magazine.length();

        int[] hash = new int[26];

        for (int i = 0; i < n2; i++) {
            hash[magazine.charAt(i) - 'a']++;
        }

        for (int i = 0; i < n1; i++) {
            hash[ransomNote.charAt(i) - 'a']--;
            if (hash[ransomNote.charAt(i) - 'a'] < 0) {
                return false;
            }
        }
        return true;
    }
}

15. 三数之和

题目链接

哈希法 + 双指针 -> 实现 O(n^2) 复杂度

不能有重复的三元组，但三元组内的元素是可以重复的！

思路：
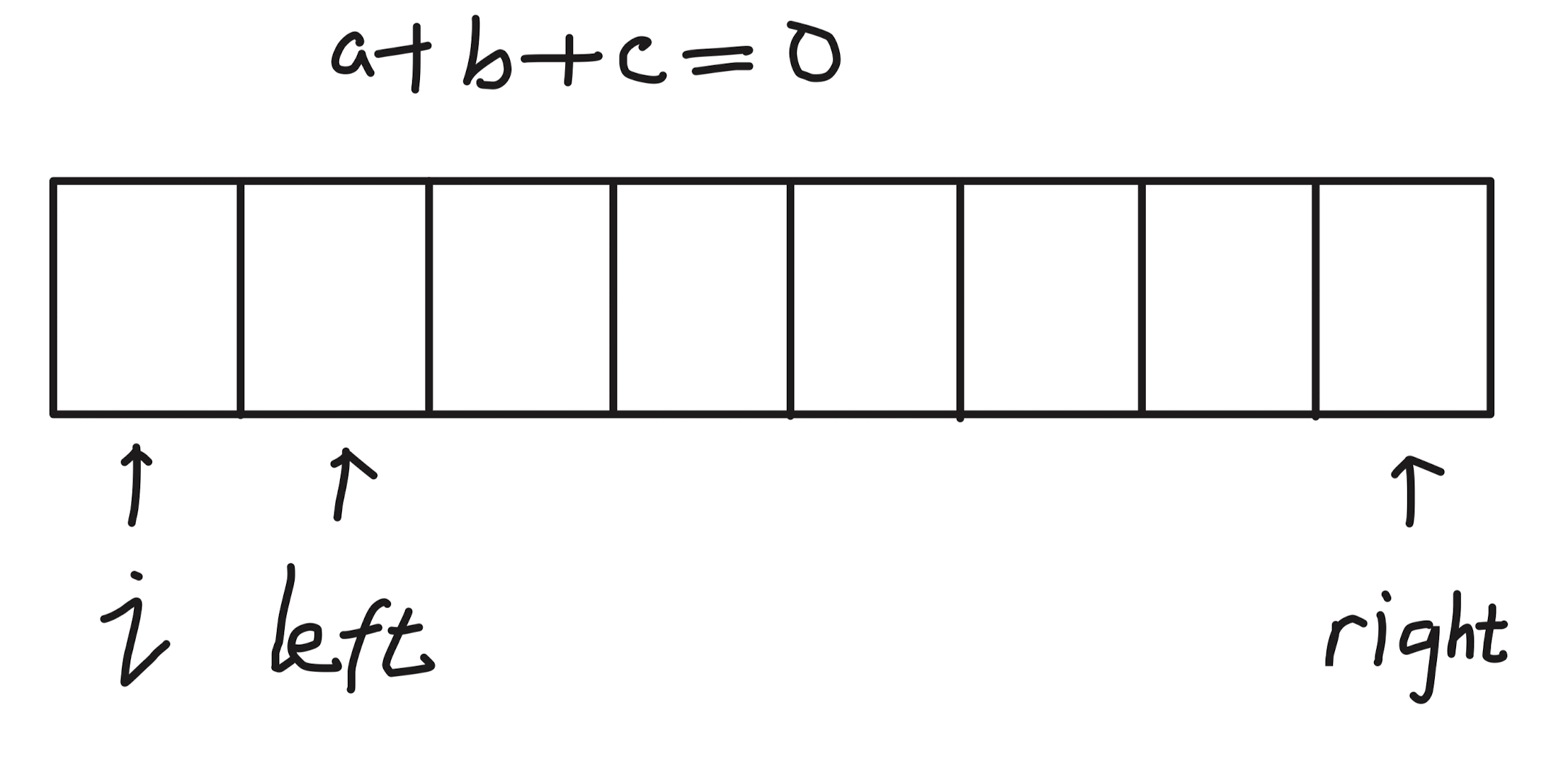
枚举 a
b 和 c 用左右指针

易错点：

三个去重：
- a 去重：nums[i] == nums[i - 1]。如 -1 -1 -1 2
如果写成 nums[i] == nums[i + 1]，则是要求三个数不能有重复的
- b 和 c 去重：nums[right] == nums[right + 1] 和 nums[left] == nums[left - 1]。如 -1 1 1 2 2

在这里插入图片描述

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        // 3 <= nums.length <= 3000
        int n = nums.length;

        // 先排序
        Arrays.sort(nums);

        List<List<Integer>> result = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            // 剪枝：排序之后如果第一个元素已经大于零，那么无论如何组合都不可能凑成三元组，直接返回结果就可以了
            if (nums[i] > 0) {
                return result;
            }
                        
            // 给 a 去重
            if (i > 0 && nums[i] == nums[i - 1] || i >= n - 2) {
                continue;
            }
            int left = i + 1;
            int right = n - 1;
            while (left < right) {
                if (nums[i] + nums[left] + nums[right] > 0) {
                    right--;
                } else if (nums[i] + nums[left] + nums[right] < 0) {
                    left++;
                } else {
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    left++;
                    right--;

                    // 给 b 和 c 去重
                    while (left < right && nums[right] == nums[right + 1]) {
                        right--;
                    }
                    while (left < right && nums[left] == nums[left - 1]) {
                        left++;
                    }
                }
            }
        }

        return result;
    }
}

18. 四数之和

题目链接

在三数之和的 for i 循环外面套一层 for k 循环即可

注意和三数之和不一样的，一个是本题不是要求等于 0 是等于 target ，另一个是本体数组长度可以最小为 1

题目非搞一个 long 恶心人
nums = [1000000000,1000000000,1000000000,1000000000]
target = -294967296
long sum = (long) nums[k] + nums[i] + nums[left] + nums[right];

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        // 1 <= nums.length <= 200
        int n = nums.length;

        // 先排序
        Arrays.sort(nums);

        List<List<Integer>> result = new ArrayList<>();
        for (int k = 0; k < n; k++) {
            // 剪枝
            if (nums[k] > target && target > 0) {
                break;
            }
            // 去重
            if (k > 0 && nums[k] == nums[k - 1]) {
                continue;
            }

            for (int i = k + 1; i < n; i++) {
                // 二级剪枝，将 nums[k] + nums[i] 当成一个整体
                if (nums[k] + nums[i] > target && target > 0) {
                    break;
                }
                // 二级去重
                if (i > k + 1 && nums[i] == nums[i - 1]) {
                    continue;
                }

                int left = i + 1;
                int right = n - 1;
                while (left < right) {
                    long sum = (long) nums[k] + nums[i] + nums[left] + nums[right];
                    if (sum > target) {
                        right--;
                    } else if (sum < target) {
                        left++;
                    } else {
                        result.add(Arrays.asList(nums[k], nums[i], nums[left], nums[right]));
                        left++;
                        right--;

                        // 给 b 和 c 去重
                        while (left < right && nums[right] == nums[right + 1]) {
                            right--;
                        }
                        while (left < right && nums[left] == nums[left - 1]) {
                            left++;
                        }
                    }                
                }
            }
        }      
        return result;
    
    }
}

哈希法总结

见之前总结