递归程序设计

1.题目分析
1.一个人赶着鸭子去每个村庄卖，每经过一个村子卖去所赶鸭子的一半又一只。这样他经过了七个村子后还剩两只鸭子，问他出发时共赶多少只鸭子？经过每个村子卖出多少只鸭子？
分析：设置唯一的出口，当村庄编号为7时，跳出递归。
2.角谷定理。输入一个自然数，若为偶数，则把它除以2，若为奇数，则把它乘以3加1。经过如此有限次运算后，总可以得到自然数值1。求经过多少次可得到自然数1。
分析：设置唯一的出口，当自然数变为1时，跳出递归。
2.算法构造
递归：
①递归出口：fun(7)=2(当村庄为7时鸭子为2)
递归体：x=fun(n+1)*2+2（随着村庄编号的减少，鸭子数量增加）
②递归出口：fun(1)(当自然数为1)
递归体：

//当自然数为偶数时，除以2，并将步数加一，并返回此时的n值
if(n%2==0)
	{
		n=n/2;
		printf("%d\n",n);
		x++;
		return fun(n);
	}
//当自然数为奇数时，乘以3加1，并将步数加一，并返回此时的n值
else if(n%2==1)
	{
		n=n*3+1;
		printf("%d\n",n);
		x++;
		return fun(n);
	}

非递归：
通过for循环算出结果，注意条件和初始值
3.算法实现
递归
第①题

#include<stdio.h>

//递归函数
int fun(int n)
{
	//定义鸭子数目x
	int x;

	//当村庄编号为7时跳出递归，并输出此时的鸭子数目
	if(n==7)
	{
		x=2;
		printf("在第%d个村庄后还剩%d只鸭子\n",n,x);
		return x;
		
	}
	//当村庄编号从0~7变化时，算出鸭子数目并进行输出
	else
	{
		x=fun(n+1)*2+2;
		printf("在第%d个村庄后还剩%d只鸭子\n",n,x);	
		return x;
	}	
}
int main()
{	
	//调用递归函数
	fun(0);
	return 0;
}

第②题

#include<stdio.h>
#include<stdlib.h>

//将x定义为全局变量就不会因递归而重新初始化
int x=0;

//递归函数
int fun(int n)
{
	//当自然数为1时输出步数，并停止递归操作
	if(n==1)
	{
		printf("Step=%d\n",x);
		
	}
	//当自然数为偶数时，除以2，并将步数加一，并返回此时的n值
	else if(n%2==0)
	{
		n=n/2;
		printf("%d\n",n);
		x++;
		return fun(n);
	}
	//当自然数为奇数时，乘以3加1，并将步数加一，并返回此时的n值
	else if(n%2==1)
	{
		n=n*3+1;
		printf("%d\n",n);
		x++;
		return fun(n);
	}
	
}
int main()
{
	int a;
	printf("请输入一个自然数：");
	scanf("%d",&a);
	//调用递归函数
	fun(a);
	return 0;
}

非递归
第①题

#include<stdio.h>
int main()
{
	//定义村庄编号
	int n;
	//定义鸭子数目
	int x=2;
	//通过循环算出剩余的鸭子
	for(n=7;n>0;n--)
	{
		x=x*2+2;
		printf("在第%d个村子时还剩%d只鸭子\n",n,x);
	}
}

第②题

#include<stdio.h>
int main()
{
	//定义自然数和步数
	int n;
	int x;
	printf("请输入一个自然数：");
	scanf("%d",&x);
	//通过循环算出每一步的结果并将步数依次加一
	for(n=0;x!=1;n++)
	{
		if(x%2==0)
		{
			x=x/2;
			printf("%d\n",x);
		}
		else if(x%2==1)
		{
			x=x*3+1;
			printf("%d\n",x);
		}
	}
	//输出步数
	printf("Step=%d\n",n);
}

运行结果：
递归：
第一题：

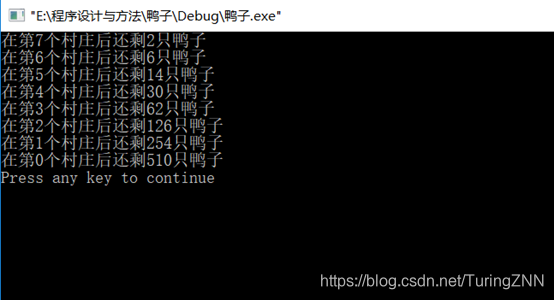
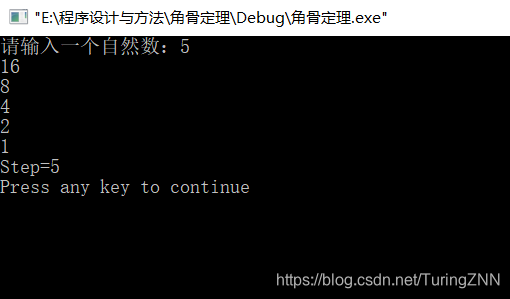
第二题：

非递归：
第一题：

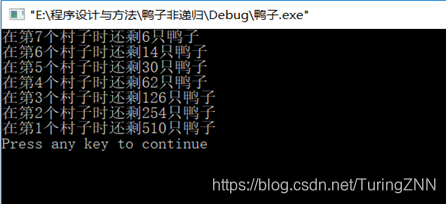
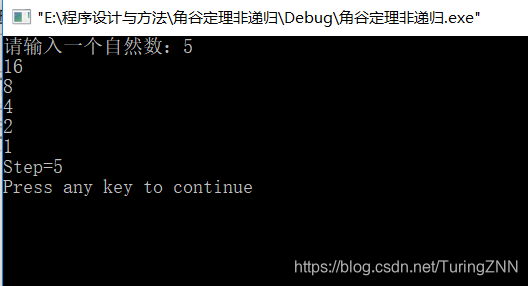
第二题：

5.经验归纳
在这次上机中让我对递归有了新的认识，本来以为很简单，后来发现没有想像中的简单，并且还出现了一些问题，在第一题中，忘记返回鸭子的数值，导致结果错误，为一串乱码，后来经过调整得出结果，在第二题中，输出步数是一个让我纠结很久的地方，因为递归会反复调用，那么我所定义的步数x会不停的被刷新，那么值就一直没有变化，后来将步数x定义为全局变量，得出正确结果，虽然在有错误时心情很烦躁，但是还是要坚持不断地调试，最后得出结果。