求N个数的最大公约数和最小公倍数

一·题目要求
基本要求： 求N个数的最大公约数和最小公倍数。用C或C++或java或python语言实现程序解决问题。
1.程序风格良好(使用自定义注释模板)
2.提供友好的输入输出，并进行输入数据的正确性验证。
二·题目分析
先算出两个数的最大公约数，再用最大公约数与第三个求最大公约数，直到第N个，用循环判断N个数中是否有1，若有1，则在新数组b[j]中去掉1，再求出没有1的数组b[j]里的最大公约数，算出N个数的乘积，用乘积除以最大公约数的j-1次方，得出最小公倍数。
三·编译结果

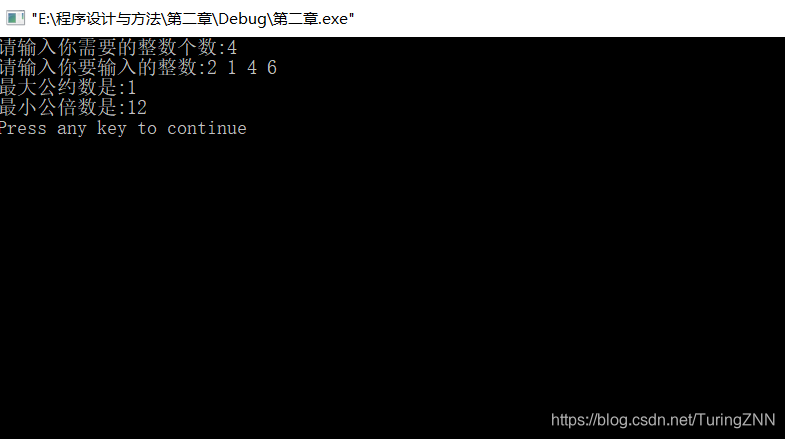
四·调试结果
运行到光标处无法输出，c值出现问题，往上发现是循环的问题，应为i<n，而不是n-1

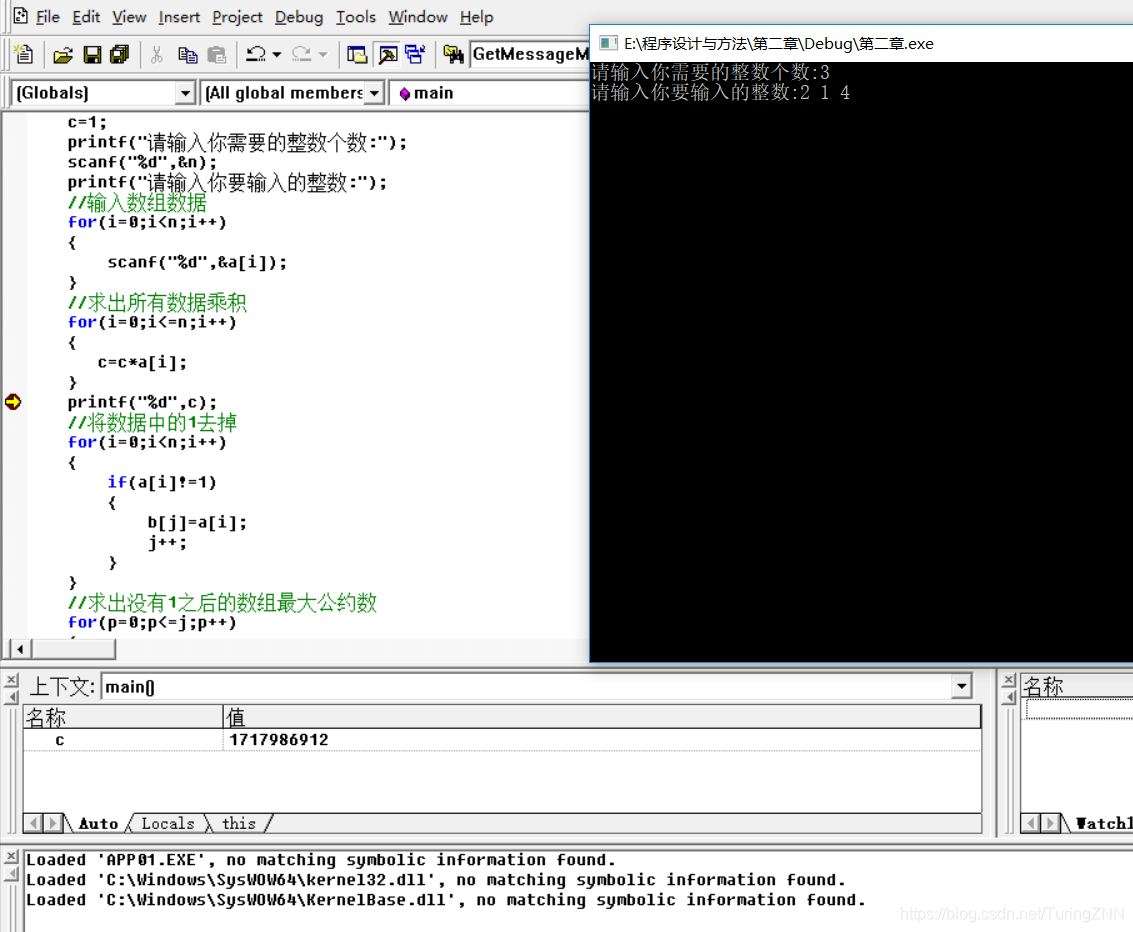
五·测试结果
重新写了一段代码测试数组乘积是否正确

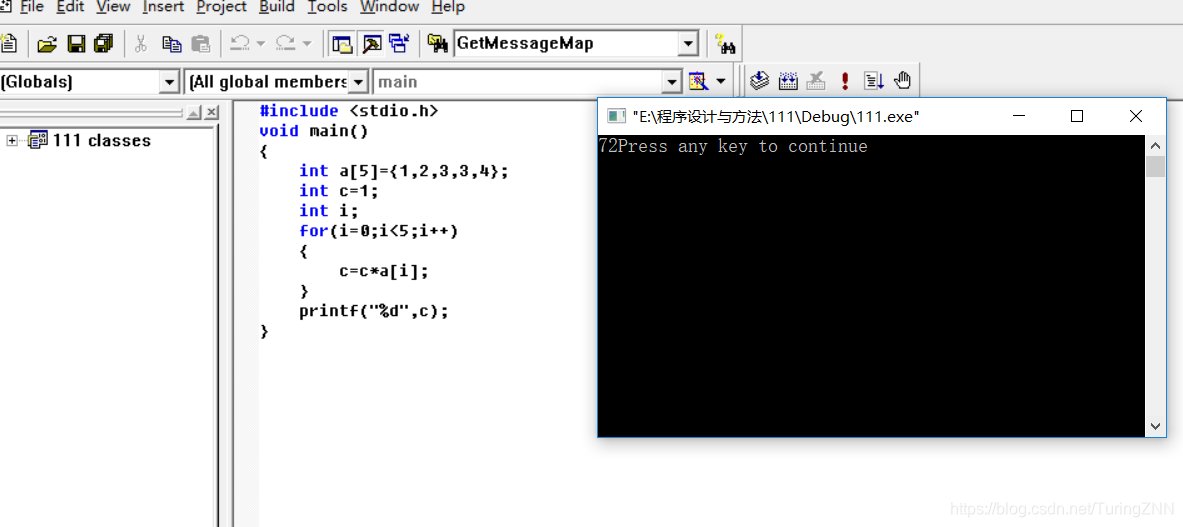
六·程序实现

#include <stdio.h>
#include <math.h>

//辗转相除法嵌套
//自定义函数求两数的最大公约数
int divisor (int a,int b)    
{
  int  temp; 
//比较求出最大值和最小值
  if(a<b)            
    { temp=a;a=b;b=temp;}
//通过循环求两数的余数，直到余数为0 
   while(b!=0)           
    {
      temp=a%b;
      a=b;             
      b=temp;
    }
//返回最大公约数到调用函数处 
  return (a);           
} 

void main()
{
	int a[10],b[10];
	int n,m,i,j,p,q,c,d;
	j=0;
	c=1;
	printf("请输入你需要的整数个数:");
	scanf("%d",&n);
	printf("请输入你要输入的整数:");
	//输入数组数据
	for(i=0;i<n;i++)
	{
		scanf("%d",&a[i]);
	}
	//求出所有数据乘积
    for(i=0;i<n;i++)
	{
       c=c*a[i];
	}
	//将数据中的1去掉
    for(i=0;i<n;i++)
	{
		if(a[i]!=1)
		{
			b[j]=a[i];
			j++;
		}
	}
	//求出没有1之后的数组最大公约数
	for(p=0;p<=j;p++)
	{
		q=divisor(b[p],b[p+1]);
		b[p+1]=q;
	}
	//求出最大公约数
    for(i=0;i<n;i++)
	{
		m=divisor(a[i],a[i+1]);
		a[i+1]=m;   
	}
	printf("最大公约数是:%d\n",m);
	//求出最小公倍数
	d=c/(pow(q,(j-1)));
	printf("最小公倍数是:%d\n",d);
}

七·经验总结
在这次实践中，开始是毫无头绪，但是后来经过思考，想出了解决办法。在程序运行过程中，我发现数组的乘积一直有错误，我就在的思考是不是我的哪个循环有错，然后我就写了一段测试代码，发现没有错误，后来我发现先后顺序不对，要在最开始的数组上面进行相乘，然后进行了调整，得出了结果。实践是检验真理的唯一标准，所以还是要积极动手才能发现自己的问题。