7
1 5
2 5
5 1
5 3
3 6
7 4
4 8
代码:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<stdio.h>
using namespace std;
const int MAXN=555;
const int n=100;
vector<int> g[MAXN];
int form[MAXN],tot;
bool use[MAXN];
bool match(int x){
for(int i=0;i<g[x].size();i++){
if(!use[g[x][i]]){
use[g[x][i]]=true;
if(form[g[x][i]]==-1 || match(form[g[x][i]])){
form[g[x][i]]=x;
return x;
}
}
}
}
int hungary(){
tot=0;
memset(form,255,sizeof(form));
for(int i=1;i<=n;i++){
memset(use,0,sizeof(use));
if(match(i))
++tot;
}
return tot;
}
int main()
{
int N;
cin>>N;
int a,b;
int ans=0;
for(int i=1;i<=N;i++)
{
cin>>a>>b;
g[a].push_back(b);
}
ans=hungary();
cout<<ans<<endl;
}




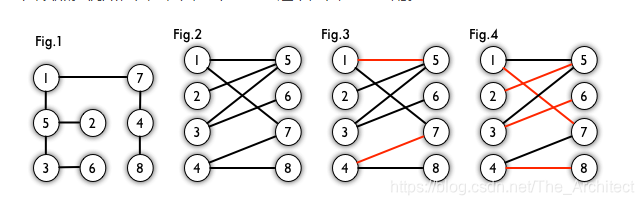
 本文深入探讨了匈牙利算法在解决二分图最大匹配问题中的应用,通过具体的代码实现展示了算法的高效性和实用性。文章首先介绍了匈牙利算法的基本原理,随后通过实例演示了如何使用该算法寻找二分图的最大匹配,最后通过代码实现进一步解释了算法的具体操作流程。
本文深入探讨了匈牙利算法在解决二分图最大匹配问题中的应用,通过具体的代码实现展示了算法的高效性和实用性。文章首先介绍了匈牙利算法的基本原理,随后通过实例演示了如何使用该算法寻找二分图的最大匹配,最后通过代码实现进一步解释了算法的具体操作流程。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








