<think>我们使用树链剖分（重链剖分）将树分割成链，然后利用DFS序（实际上是剖分后的DFS序）将树结构转化为线性序列，然后使用线段树维护序列上的权值。这样，子树查询就转化为区间查询，节点更新就转化为单点更新。
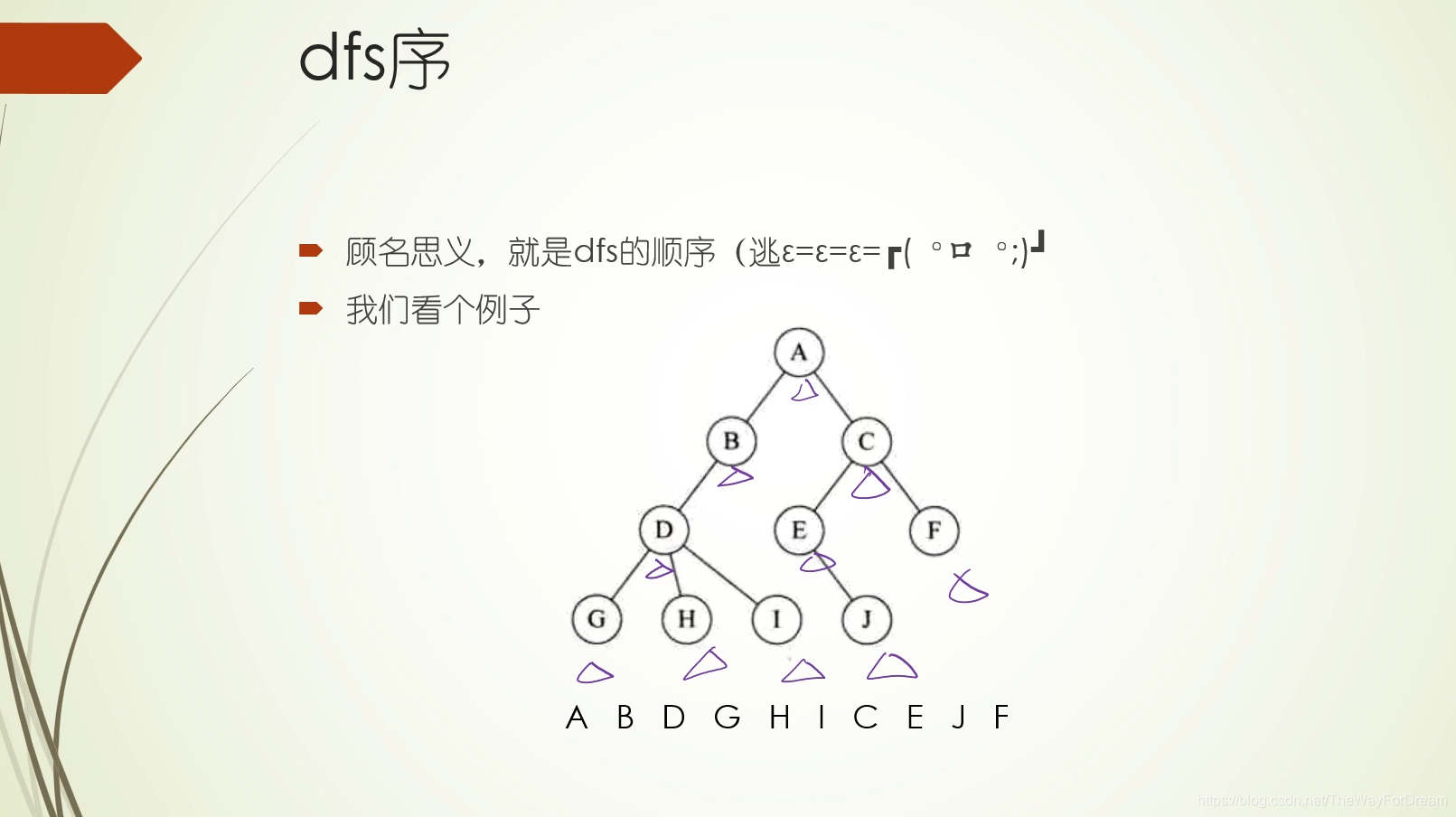
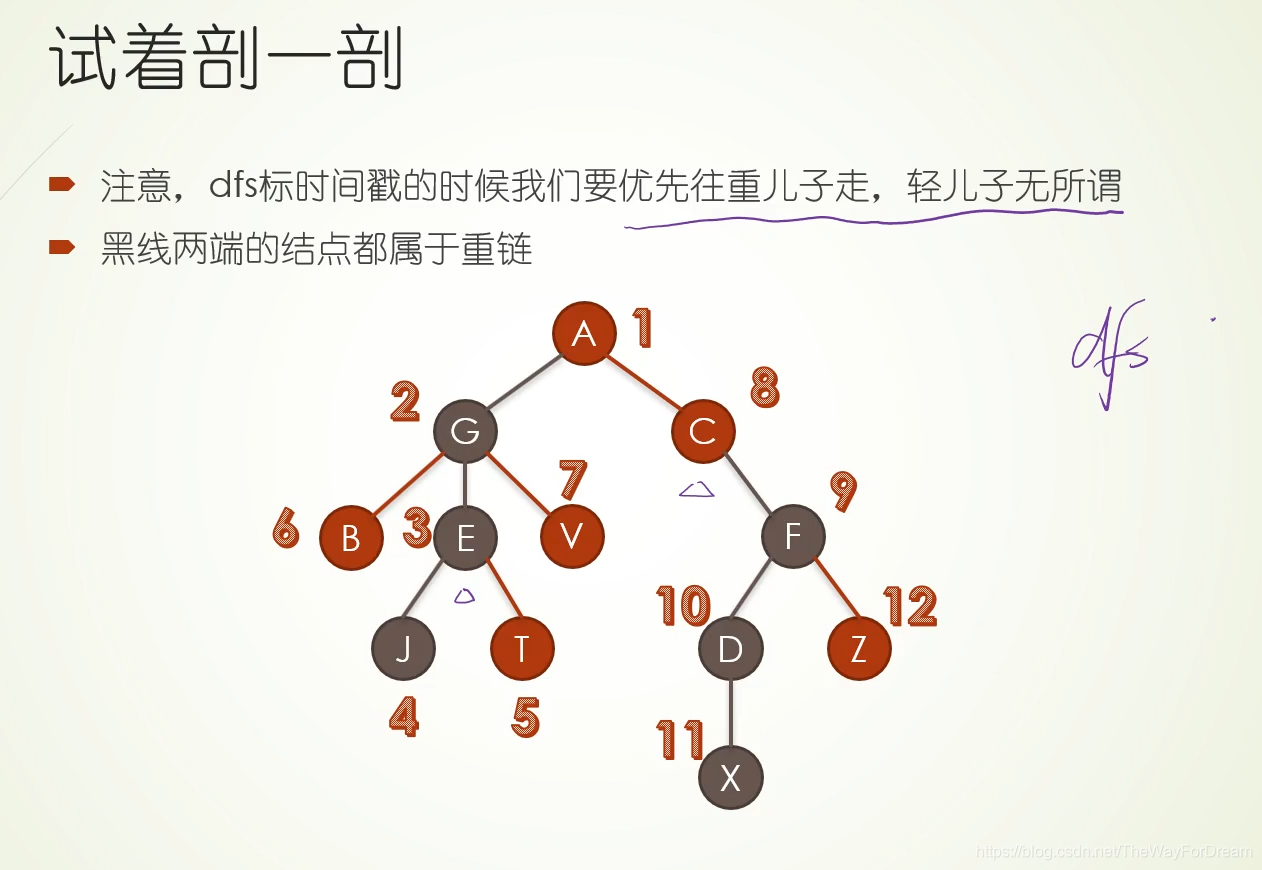
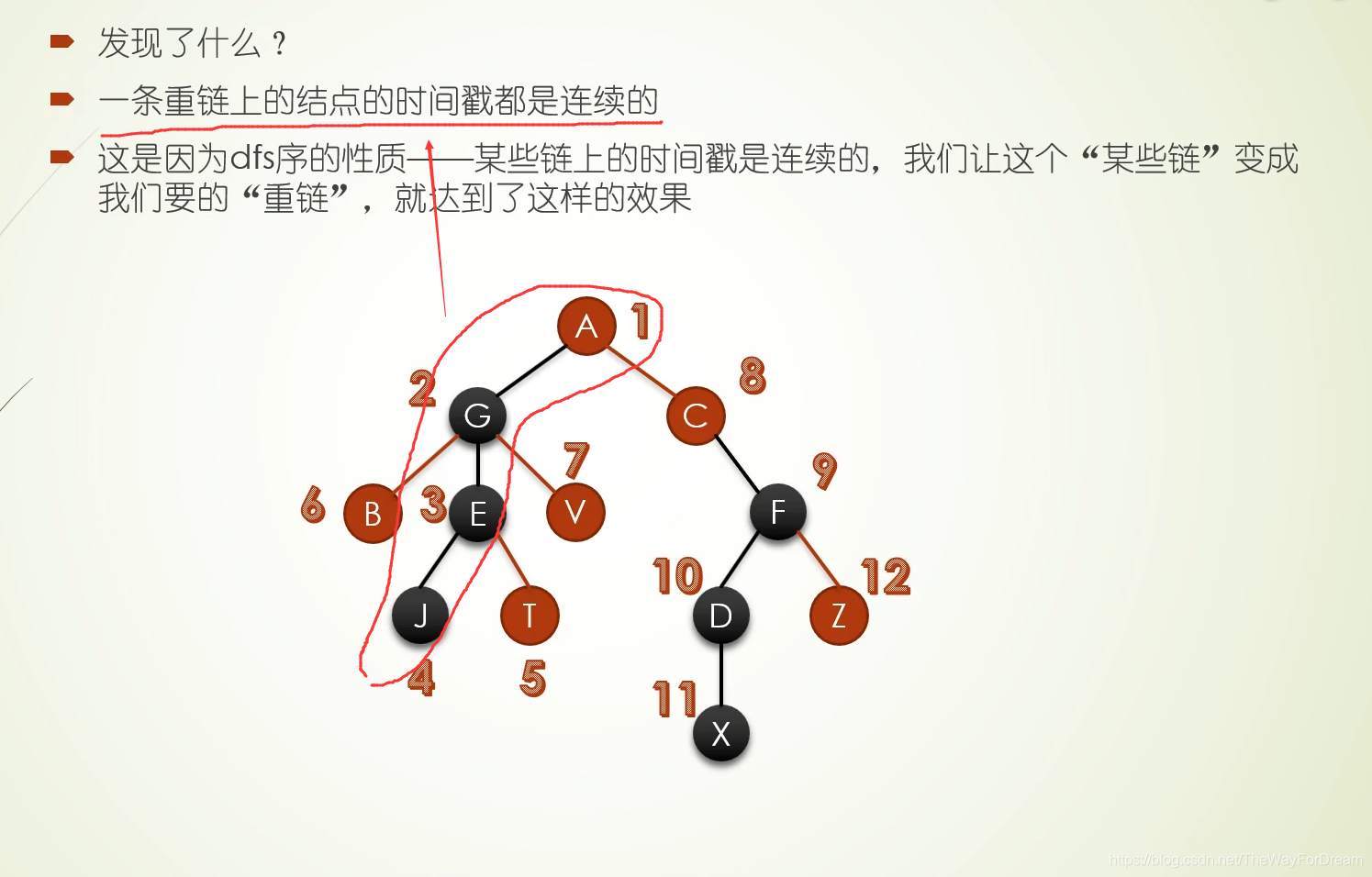
树链剖分的DFS序：在剖分DFS中，我们优先遍历重儿子，这样保证重链上的节点在DFS序中是连续的。同时，每个子树在DFS序中也是连续的（因为DFS遍历子树时是连续的）。因此，子树查询可以转化为区间查询。
步骤：
1. 第一次DFS：计算每个节点的父节点、深度、重儿子、子树大小。
2. 第二次DFS：确定DFS序（时间戳），同时记录每个节点所在链的顶端节点（用于路径查询，但本题只需要子树查询，所以这一步可以简化，但我们还是按标准剖分来做）。
3. 建立线段树：在DFS序上建立线段树，支持单点更新和区间求和。
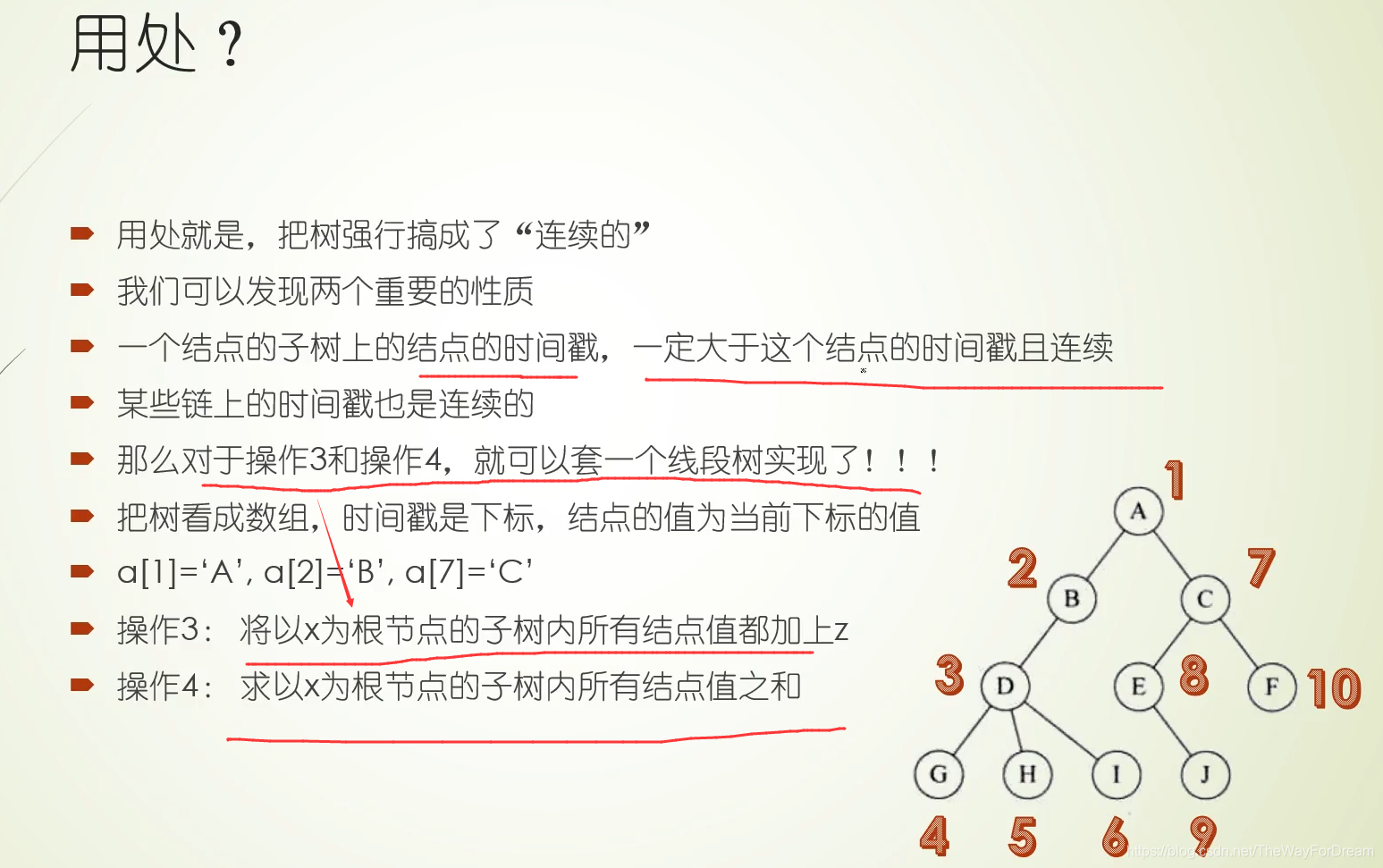
子树查询：对于节点u，其子树对应的区间为[in[u], out[u]]（即DFS进入和退出的时间戳）。注意：在树链剖分中，由于优先遍历重儿子，子树节点在DFS序中仍然是连续的。
因此，我们可以使用线段树来维护这个区间和。
伪代码（Python风格）如下：
```python
import sys
sys.setrecursionlimit(200000)
class SegmentTree:
def __init__(self, data):
self.n = len(data)
self.size = 1
while self.size < self.n:
self.size *= 2
self.tree = [0] * (2 * self.size)
# 构建线段树，初始数据
for i in range(self.n):
self.tree[self.size + i] = data[i]
for i in range(self.size - 1, 0, -1):
self.tree[i] = self.tree[2*i] + self.tree[2*i+1]
def update(self, index, value):
# 单点更新：将位置index的值改为value（注意：这里是直接赋值，如果是增加则需要调整）
# 但通常我们支持增加一个差值，这里按需求，我们假设是更新为新的值，所以需要知道旧值？或者我们设计为增加一个增量？
# 根据问题，节点改变权值，我们可以用增量更新。但为了通用，这里我们实现为单点设置值，但需要知道原值？或者我们设计为传入增量（更符合动态更新）。
# 这里我们实现为增量更新（delta）
# index: 原始数组中的位置（0-indexed）
pos = index + self.size
self.tree[pos] += value # 增加一个增量
while pos > 1:
pos //= 2
self.tree[pos] = self.tree[2*pos] + self.tree[2*pos+1]
def query(self, l, r):
# 区间查询 [l, r] (闭区间)
l += self.size
r += self.size
res = 0
while l <= r:
if l % 2 == 1:
res += self.tree[l]
l += 1
if r % 2 == 0:
res += self.tree[r]
r -= 1
l //= 2
r //= 2
return res
# 树链剖分部分
n = 100000
graph = [[] for _ in range(n+1)]
# 第一次DFS：计算父节点、深度、子树大小、重儿子
parent = [0] * (n+1)
depth = [0] * (n+1)
size = [0] * (n+1)
heavy = [-1] * (n+1) # 重儿子，初始化为-1
def dfs1(u, p, d):
parent[u] = p
depth[u] = d
size[u] = 1
max_size = 0
for v in graph[u]:
if v == p:
continue
dfs1(v, u, d+1)
size[u] += size[v]
if size[v] > max_size:
max_size = size[v]
heavy[u] = v
# 第二次DFS：确定DFS序（时间戳）和重链的顶端
head = [0] * (n+1) # 链的顶端节点
pos = [-1] * (n+1) # 节点在DFS序中的位置（时间戳）
cur_time = 0
def dfs2(u, h):
global cur_time
head[u] = h
pos[u] = cur_time
cur_time += 1
# 如果有重儿子，先遍历重儿子
if heavy[u] != -1:
dfs2(heavy[u], h)
for v in graph[u]:
if v == parent[u] or v == heavy[u]:
continue
dfs2(v, v) # 轻儿子，自己作为新链的顶端
# 初始化
def init_tree(root):
dfs1(root, 0, 0)
dfs2(root, root)
# 初始化一个长度为n（节点数）的数组，初始权值，假设为0，或者根据实际输入
arr = [0] * n # 注意：节点从1开始，时间戳从0到n-1
seg_tree = SegmentTree(arr)
return seg_tree, pos, head # 返回线段树和位置数组
# 更新节点u的权值（增加delta）
def update_node(seg_tree, u, delta):
idx = pos[u] # 节点u在线段树中的位置
seg_tree.update(idx, delta)
# 查询子树u的权值和：子树u对应的区间为 [pos[u], pos[u]+size[u]-1] ？注意：在树链剖分的DFS序中，子树u的节点在区间[pos[u], pos[u]+size[u]-1]内吗？
# 实际上，在第二次DFS中，我们优先遍历重儿子，然后轻儿子。子树u的DFS序区间是连续的，因为递归完子树后才会遍历下一个子树。所以子树u的区间为 [pos[u], pos[u] + size[u] - 1]。
def query_subtree(seg_tree, u):
l = pos[u]
r = pos[u] + size[u] - 1
return seg_tree.query(l, r)
# 注意：这里线段树的区间是[0, n-1]，所以直接使用pos[u]和pos[u]+size[u]-1即可。
```
### 注意点：
- 树链剖分的DFS序保证了每个子树是连续的，所以我们可以用区间[pos[u], pos[u]+size[u]-1]表示子树。
- 线段树支持区间求和和单点更新（增量更新）。如果节点权值改变为新的值，则需要计算增量（新值-旧值）然后更新。
### 时间复杂度：
- 预处理：两次DFS，O(n)
- 更新：O(log n)
- 查询：O(log n)
### 与树状数组+DFS序的对比：
- 树状数组+DFS序（普通DFS序）同样可以做到，且树状数组常数更小，代码更简单。
- 树链剖分的主要优势在于可以同时支持路径查询（而不仅仅是子树查询）。如果问题需要查询路径上的权值和，树链剖分就更有优势。
### 总结：
对于子树查询，树状数组+普通DFS序已经足够高效。树链剖分+线段树也可以实现，但代码稍复杂，但扩展性强（支持路径查询）。本题要求子树查询，两种方法均可，但树链剖分在这里有点“大材小用”。
§§相关问题§§
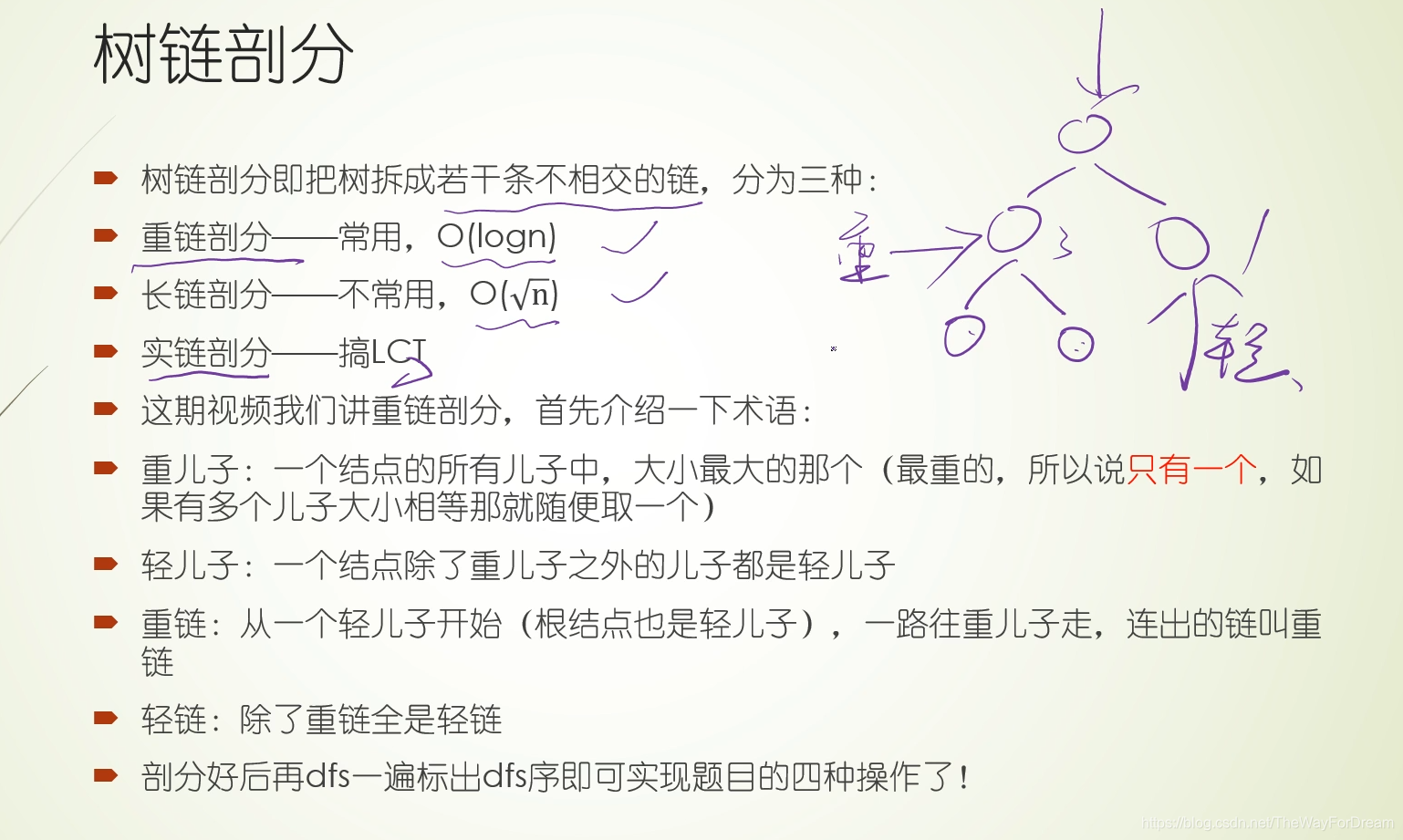
1. 树链剖分中重链和轻链的作用是什么？为什么优先遍历重儿子？
2. 除了子树查询，树链剖分还能支持哪些类型的查询和操作？
3. 如果树的结构是动态变化的（如添加或删除边），如何维护树链剖分？
4. 线段树和树状数组在实现子树查询时各自的优缺点是什么？</think>对于树结构不变、节点数不超过 100,000 的场景，使用 **线段树 + 树链剖分** 是高效支持子树权值查询和节点权值更新的解决方案。树链剖分将树结构转化为线性序列，线段树则提供高效的区间查询和单点更新能力。
### 解决方案步骤：
1. **树链剖分预处理**：
- **第一次 DFS**：计算每个节点的父节点、深度、子树大小（`size[u]`）和重儿子（子树最大的子节点）
- **第二次 DFS**：生成 DFS 序（优先遍历重儿子），记录节点入序时间戳 `dfn[u]` 和子树结束时间 `end[u]`（子树节点在 DFS 序中连续）
2. **线段树构建**：
- 基于 DFS 序构建线段树，叶子节点存储原始节点权值
- 支持单点更新（节点权值修改）和区间查询（子树权值和）
### 代码实现（Python 风格）
```python
import sys
sys.setrecursionlimit(200000)
class SegmentTree:
def __init__(self, n):
self.n = n
self.size = 1
while self.size < n:
self.size *= 2
self.tree = [0] * (2 * self.size)
def update(self, index, delta):
"""单点更新：位置 index 增加 delta"""
i = index + self.size
self.tree[i] += delta
while i > 1:
i //= 2
self.tree[i] = self.tree[2*i] + self.tree[2*i+1]
def query(self, l, r):
"""区间查询 [l, r] 的和"""
l += self.size
r += self.size
res = 0
while l <= r:
if l % 2 == 1:
res += self.tree[l]
l += 1
if r % 2 == 0:
res += self.tree[r]
r -= 1
l //= 2
r //= 2
return res
# 树链剖分预处理
n = 100000 # 最大节点数
graph = [[] for _ in range(n+1)]
parent = [0] * (n+1) # 父节点
depth = [0] * (n+1) # 深度
size = [0] * (n+1) # 子树大小
heavy = [-1] * (n+1) # 重儿子
dfn = [0] * (n+1) # DFS 入序时间戳
end = [0] * (n+1) # 子树结束时间戳
cur_time = 0
def dfs1(u, p, d):
"""第一次 DFS：计算 size/heavy"""
parent[u] = p
depth[u] = d
size[u] = 1
max_size = 0
for v in graph[u]:
if v == p: continue
dfs1(v, u, d+1)
size[u] += size[v]
if size[v] > max_size:
max_size = size[v]
heavy[u] = v
def dfs2(u, head):
"""第二次 DFS：生成 DFS 序"""
global cur_time
dfn[u] = cur_time
cur_time += 1
# 优先遍历重儿子
if heavy[u] != -1:
dfs2(heavy[u], head) # 重儿子继承当前链头
for v in graph[u]:
if v == parent[u] or v == heavy[u]:
continue
dfs2(v, v) # 轻儿子作为新链头
end[u] = cur_time - 1 # 子树结束时间
# 初始化树链剖分
def init_tree(root=1):
dfs1(root, 0, 0)
dfs2(root, root) # 根节点作为第一条链的链头
return SegmentTree(cur_time) # 创建线段树
# 更新节点 u 的权值 (新值 new_val)
def update_node(seg_tree, u, new_val, old_val):
delta = new_val - old_val
seg_tree.update(dfn[u], delta)
# 查询子树 u 的权值和
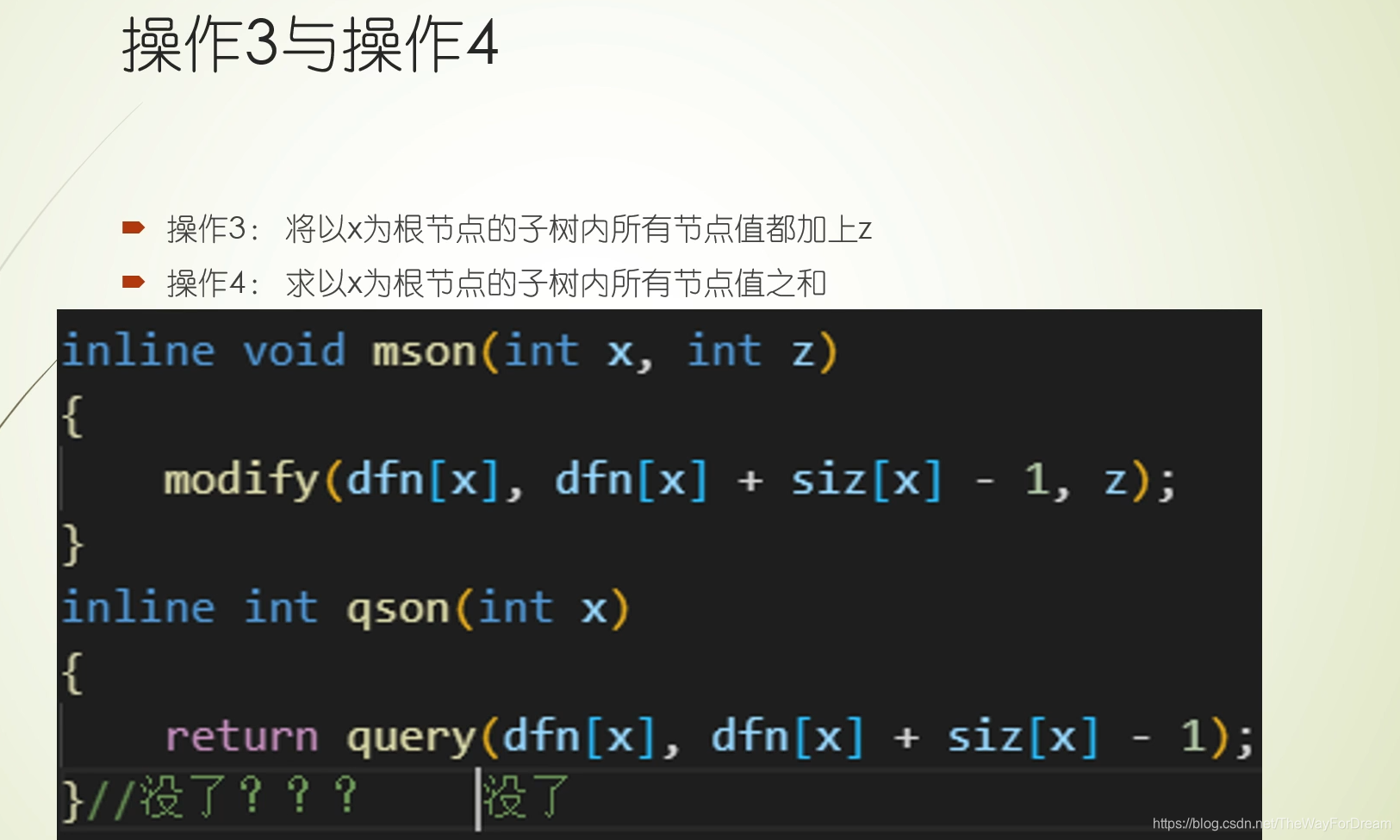
def query_subtree(seg_tree, u):
return seg_tree.query(dfn[u], end[u])
# 使用示例
if __name__ == "__main__":
# 假设树已构建在 graph 中，root=1
seg_tree = init_tree()
# 初始化节点权值 (假设存储在 node_val 数组)
for u in range(1, n+1):
seg_tree.update(dfn[u], node_val[u])
# 示例：更新节点 5 权值为 10 (旧值假设为 7)
update_node(seg_tree, 5, 10, 7)
# 示例：查询子树 3 的权值和
print(query_subtree(seg_tree, 3))
```
### 时间复杂度分析
| 操作 | 时间复杂度 | 说明 |
|--------------|------------|--------------------------|
| 树链剖分预处理 | O(n) | 两次 DFS 遍历 |
| 单点权值更新 | O(log n) | 线段树单点更新 |
| 子树权值查询 | O(log n) | 线段树区间查询 |
### 优势与适用场景
1. **树链剖分优势**：
- 将子树查询转化为 **连续区间查询**（`[dfn[u], end[u]]`）
- DFS 序连续性由重链优先遍历保证
2. **线段树优势**：
- O(log n) 高效区间求和
- 支持动态点更新
3. **扩展性**：
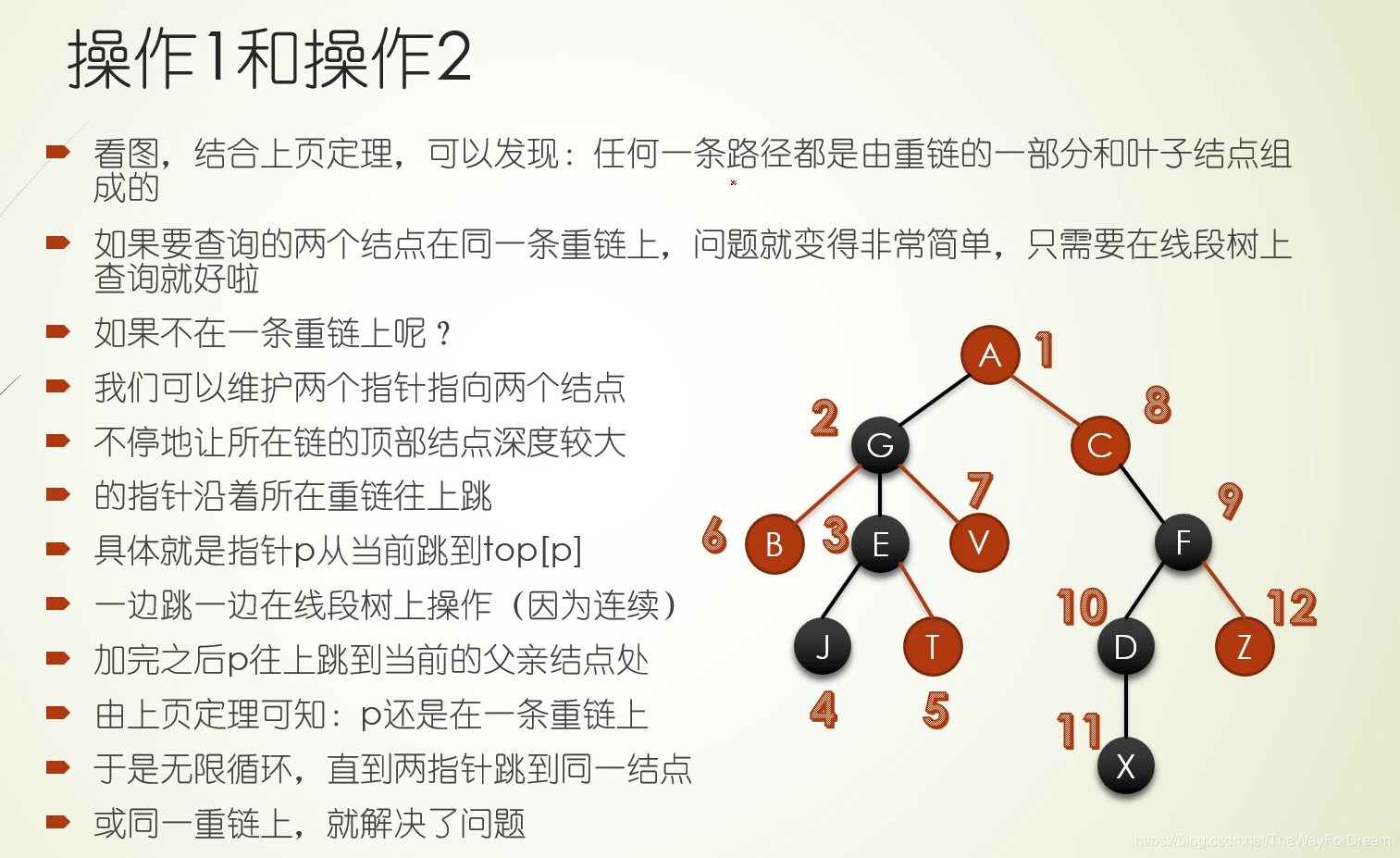
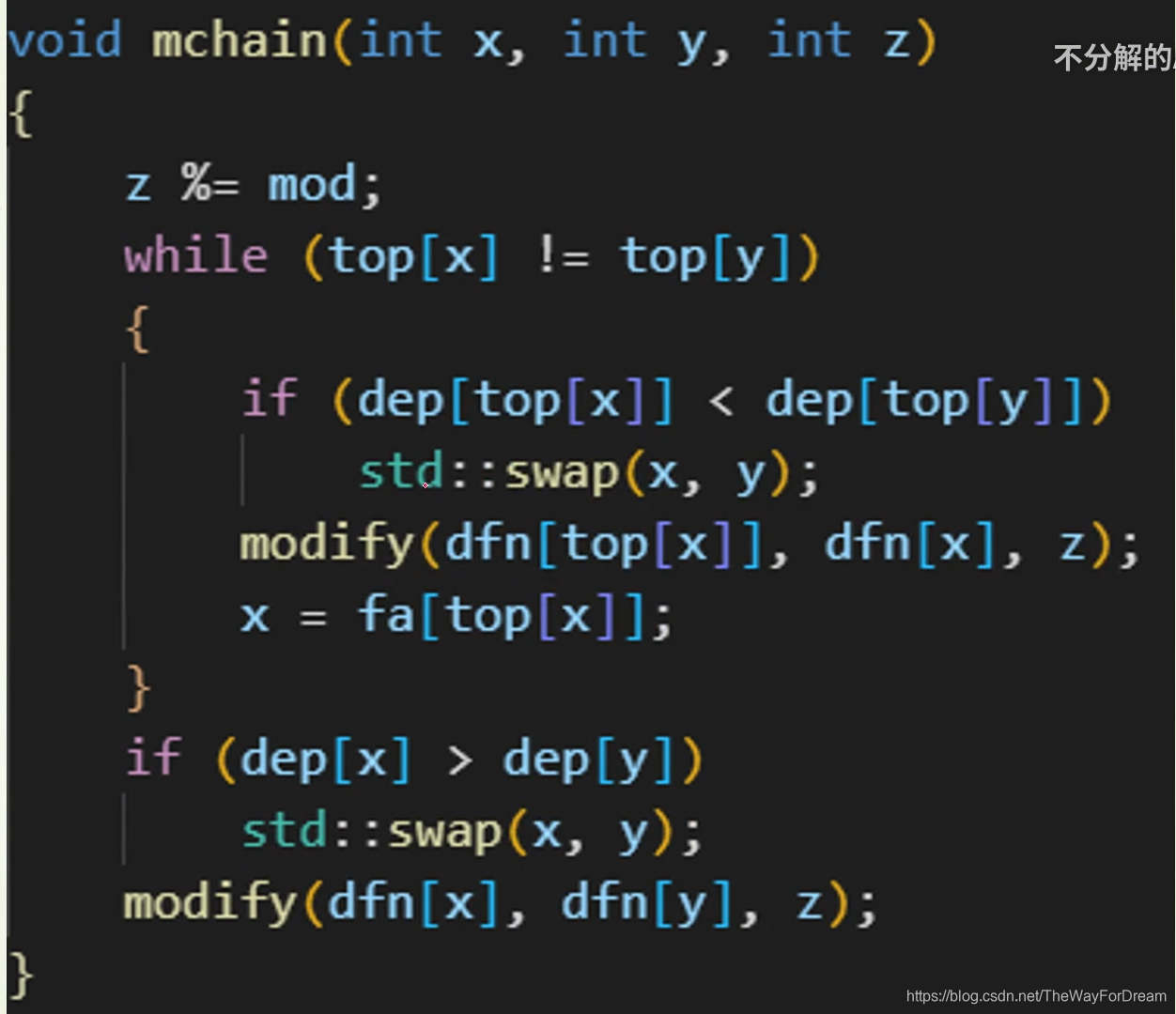
- 可扩展支持路径查询（通过跳链查询）
- 可支持其他聚合操作（最大值、最小值等）
此方案在节点数 100,000 时完全可行，预处理 O(n)，每次操作 O(log n)。
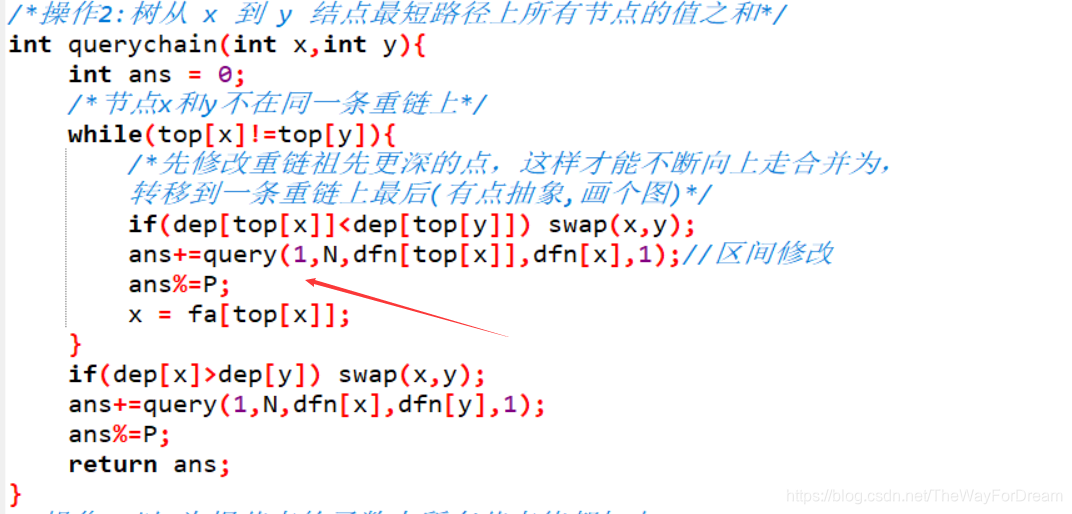
本文详细介绍了树链剖分的原理，涉及dfs序、时间戳在链式前向星和线段树中的运用，以及如何解决区间修改、查询问题。通过模板题和LCA问题实例，配合视频教学，帮助读者深入理解并掌握这一技术。
最低0.47元/天 解锁文章
扫一扫
509
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
