(CodeForces) E1,E2. Array and Segments (Easy / Hard version) (线段树||差分)

视频讲解戳这里（感觉我讲的还没这写的清楚）

传送门

题目大意：n个数，可选的m次操作，一次操作区间[l,r],使得区间中的数全都减1，问你选那几个操作可以使得该数组的最大值-最小值最大。E1，E2的区别就是一个数据大一个数据小。

解题思路：一开始是没有头绪的，这是让你选操作而不是让你操作，但是还是很容易联想到差分和线段树操作的。我们可以考虑一顿操作之后数组中必然会出现最大值和最小值，因为操作都是-1，那每个数被操作后都有可能变成最小值，对于E1的数据我们完全可以枚举每一个数为可能的最小值，只要操作区间包含这个数，我们就操做，最后扫一遍数组求的最值相减。这为什么是对的呢，因为如果最大值在他的操作区间，那就一同减一不影响结果，不在那就是极好的。

E1非常暴力的代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<cmath>
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
const int maxn=305;
struct node {
	int l,r,id;
} t[maxn];
int n,m,a[maxn],b[maxn];
int main() {
	std::ios::sync_with_stdio(0);
	cin>>n>>m;
	int mx=-inf,mi=inf;
	for(int i=1; i<=n; ++i) {
		cin>>a[i];
		mx=max(mx,a[i]);
		mi=min(mi,a[i]);
	}
	for(int i=1; i<=m; ++i) {
		cin>>t[i].l>>t[i].r;
		t[i].id=i;
	}
	vector<int> v;
	int ans=mx-mi;
	vector<int> tp;
	for(int i=1; i<=n; ++i) {
		tp.clear();
		memcpy(b,a,sizeof(a));
		for(int j=1; j<=m; ++j) {
			if(t[j].l<=i&&t[j].r>=i) {
				for(int k=t[j].l; k<=t[j].r; ++k) {
					b[k]--;
				}
				tp.push_back(t[j].id);
			}
		}
		mx=-inf,mi=inf;
		for(int i=1; i<=n; ++i) {
			mx=max(mx,b[i]);
			mi=min(mi,b[i]);
		}
		if(mx-mi>ans) {
			v=tp;
			ans=mx-mi;
		}
	}
	cout<<ans<<endl;
	cout<<v.size()<<endl;
	for(int i=0; i<v.size(); ++i) {
		cout<<v[i]<< " ";
	}
	cout<<endl;
	return 0;
}

解题思路：E2数据n直接变成了1e5但是m还是300，直接考虑，线段树的复杂度是n*mlogn,而差分是n^2,复杂度都不容乐观，我们仔细考虑一下，如果只有一个操作区间比如 1~15时，我们考虑1为最低时，操作结束后，相当于1~15都考虑过了，但我们还在不辞辛劳的枚举，做了多少无用功。

 

 

 

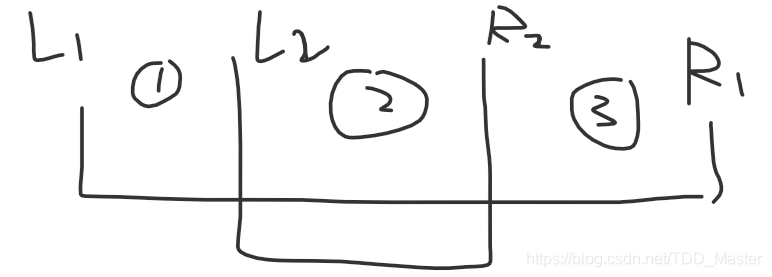
最好的应该是考虑1，2，3区间最简的，但是我们不妨直接将l1,l2,r1,r2(区间多了再去个重)加入数组，考虑这几个边界，考虑l1时，解决了1，3区间，l2时解决了2区间，虽然这样还是会有多考虑的，但是已经大大减少，而且减少了讨论，何乐不为。

线段树版代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<cmath>
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
const int maxn=1e5+5;
struct node {
	ll mx;
	ll mi;
} s[maxn<<2],pres[maxn<<2];
ll add[maxn<<2],preadd[maxn<<2];
ll a[maxn];
int n,m,le[maxn],ri[maxn];
void pushup(int rt) {
	s[rt].mx=max(s[rt<<1].mx,s[rt<<1|1].mx);
	s[rt].mi=min(s[rt<<1].mi,s[rt<<1|1].mi);
}
void build(int rt,int l,int r) {
	if(l==r) {
		s[rt].mx=a[l];
		s[rt].mi=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	build(rt<<1,l,mid);
	build(rt<<1|1,mid+1,r);
	pushup(rt);
}
void pushdown(int rt,int ln,int rn) {
	if(add[rt]) {
		add[rt<<1]+=add[rt],add[rt<<1|1]+=add[rt];
		s[rt<<1].mx+=add[rt],s[rt<<1].mi+=add[rt];
		s[rt<<1|1].mx+=add[rt],s[rt<<1|1].mi+=add[rt];
		add[rt]=0;
	}
}
void update(int L,int R,int C,int l,int r,int rt) {
	if(L<=l&&R>=r) {
		s[rt].mx+=C,s[rt].mi+=C;
		add[rt]+=C;
		return ;
	}
	int mid=(l+r)>>1;
	pushdown(rt,mid-l+1,r-mid);
	if(L<=mid) {
		update(L,R,C,l,mid,rt<<1);
	}
	if(R>mid) {
		update(L,R,C,mid+1,r,rt<<1|1);
	}
	pushup(rt);
}
int main() {
	scanf("%d%d",&n,&m);
	ll tmx=-inf,tmi=inf;
	for(int i=1; i<=n; ++i) {
		scanf("%lld",a+i);
		tmx=max(tmx,a[i]);
		tmi=min(tmi,a[i]);
	}
	vector<int> tt;
	for(int i=1; i<=m; ++i) {
		scanf("%d%d",le+i,ri+i);
		tt.push_back(le[i]);
		tt.push_back(ri[i]);
	}
	sort(tt.begin(),tt.end());
	tt.erase(unique(tt.begin(),tt.end()),tt.end());
	
	int ans=tmx-tmi;
	vector<int> v,tp;
	build(1,1,n);
	memcpy(pres,s,sizeof(s)),memcpy(preadd,add,sizeof(add));
	for(int i=0; i<(int)tt.size(); ++i) {
		tp.clear();
		memcpy(s,pres,sizeof(pres)),memcpy(add,preadd,sizeof(preadd));
		for(int j=1; j<=m; ++j) {
			if(le[j]<=tt[i] && ri[j]>=tt[i]) {
				update(le[j],ri[j],-1,1,n,1);
				tp.push_back(j);
			}
		}
		if(s[1].mx-s[1].mi>ans) {
			ans=s[1].mx-s[1].mi;
			v=tp;
		}
	}
	cout<<ans<<endl;
	cout<<v.size()<<endl;
	for(int i=0; i<v.size(); ++i) {
		cout<<v[i]<<" ";
	}
	cout<<endl;

	return 0;
}

差分版代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<cmath>
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
const int maxn=1e5+5;
using namespace std;
int n,m,le[maxn],ri[maxn],a[maxn];
int main() {
	std::ios::sync_with_stdio(0);
	cin>>n>>m;
	int mx=-inf,mi=inf,l,r;
	for(int i=1; i<=n; ++i) {
		cin>>a[i];
		mx=max(mx,a[i]);
		mi=min(mi,a[i]);
	}
	int res=mx-mi;
	vector<int> v,tp,ans;
	for(int i=1; i<=m; ++i) {
		cin>>le[i]>>ri[i];
		v.push_back(le[i]),v.push_back(ri[i]);
	}
	sort(v.begin(),v.end());
	v.erase(unique(v.begin(),v.end()),v.end());
	int sum[maxn];
	for(int i=0; i<(int)v.size(); ++i) {
		tp.clear();
		memset(sum,0,sizeof(sum));
		for(int j=1; j<=m; ++j) {
			if(le[j]<=v[i]&&ri[j]>=v[i]){
				tp.push_back(j);
				sum[le[j]]--;
				sum[ri[j]+1]++;
			}
		}
		mx=-inf,mi=inf;
		for(int i=1;i<=n;++i){
			sum[i]+=sum[i-1];
			mx=max(mx,sum[i]+a[i]);
			mi=min(mi,sum[i]+a[i]);
		}
		if(mx-mi>res){
			res=mx-mi;
			ans=tp;
		}
	}
	cout<<res<<endl;
	cout<<(int)ans.size()<<endl;
	for(int i=0;i<(int)ans.size();++i){
		cout<<ans[i]<<" ";
	}
	cout<<endl;

	return 0;
}

虽然都能过，但是差分的效率比线段树高的不是一点半点(可能线段树写的烂，还有这里memcpy花的时间多)

线段树 

差分