【数学建模】清风数模正课4 拟合算法

拟合算法

在插值算法中，我们得到的曲线一定是要经过所有的函数点的；而用拟合所得到的曲线则不一样，拟合问题中，不需要得到的曲线一定经过给定的点。

拟合的目的是寻求一个函数曲线，使得该曲线在某种准则下与所有的数据点最为接近，也就是曲线拟合地最好。

为了确定拟合曲线，我们要使用最小二乘法：

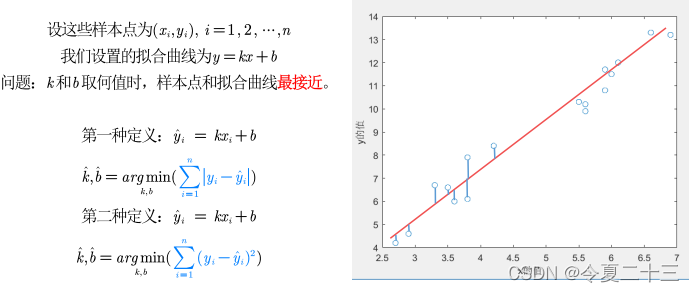
 第一种定义方法有绝对值，不容易求导，因此计算比较复杂。而第二种方法，就是最小二乘法，可以理解为求得样本点和拟合曲线间距之差的二次方之和，并且这个和要是最小的。

在这里为什么不用四次方或奇数次方呢？

1. 使用四次方的话，极端数据将对拟合曲线产生很大影响；

2. 使用奇数次方的话，误差很可能会正负相抵。

求解最小二乘法

 相关代码

clear;clc
load  data1
plot(x,y,'o')
% 给x和y轴加上标签
xlabel('x的值')
ylabel('y的值')
n = size(x,1);
k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
hold on % 继续在之前的图形上来画图形
grid on % 显示网格线

% % 画出y=kx+b的函数图像 plot(x,y)
% % 传统的画法：模拟生成x和y的序列，比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7  % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b  % k和b都是已知值
% plot(xx,yy,'-')

% 匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数，可以是一个，也可以是多个，用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子
%  z=@(x,y) x^2+y^2; 
%  z(1,2) 
% % ans =  5
% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval =  [xmin xmax] 表示定义域的范围

f=@(x) k*x+b;
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','SouthEast')

评价拟合的好坏

 这里提到的线性函数，指的是对参数为线性，也就是k和b只能以一次方出现，而且不能互相计算或复合。

相关代码

y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2)  % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR   % 5.6843e-14  =   5.6843*10^-14   matlab浮点数计算的一个误差
R_2 = SSR / SST