AcWing 1015. 摘花生JAVA（数字三角形模型DP）

最新推荐文章于 2024-10-01 18:52:56 发布

原创最新推荐文章于 2024-10-01 18:52:56 发布 · 326 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划

AcWing算法提高专栏收录该内容

10 篇文章

订阅专栏

本文介绍了一个使用动态规划解决网格中从左上角到右下角路径最大值的问题，通过Java实现，适用于类似LeetCode上的不同路径系列题目。代码详细展示了如何初始化网格，计算每一步的最大值，并最终返回从起点到终点的最大路径值。

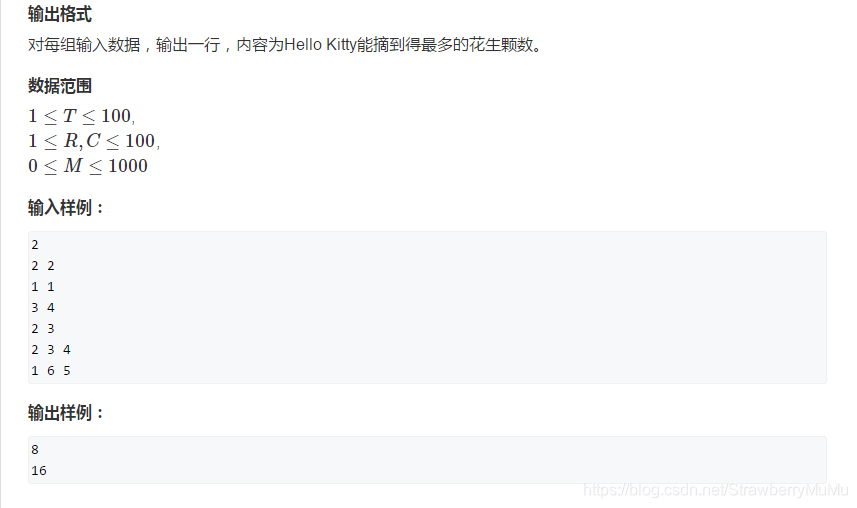
类似：leetcode62. 不同路径；63. 不同路径 II


import java.io.*;
import java.lang.*;

class Main{
    static int n = 0, R = 0, C = 0, N = 110;
    static int[][] nums = new int[N][N];
    static int[][] max = new int[N][N];
    static int getMax(){
        
        for(int i = 1; i <= R; ++i){
            for(int j = 1; j <= C; ++j){
                max[i][j] = Math.max(max[i - 1][j], max[i][j - 1]) + nums[i][j];
            }
        }
        return max[R][C];
    }
    public static void main(String[] args)throws Exception{
        BufferedReader buf = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.valueOf(buf.readLine());
        
        while(n-- != 0){
            String[] params = buf.readLine().split(" ");
            R = Integer.valueOf(params[0]);
            C = Integer.valueOf(params[1]);
            for(int i = 1; i <= R; ++i){
                String[] info = buf.readLine().split(" ");
                for(int j = 1; j <= C; ++j){
                    nums[i][j] = Integer.valueOf(info[j - 1]);
                }
            }
            int res = getMax();
            System.out.println(res);
        }
    }
}