最短路问题
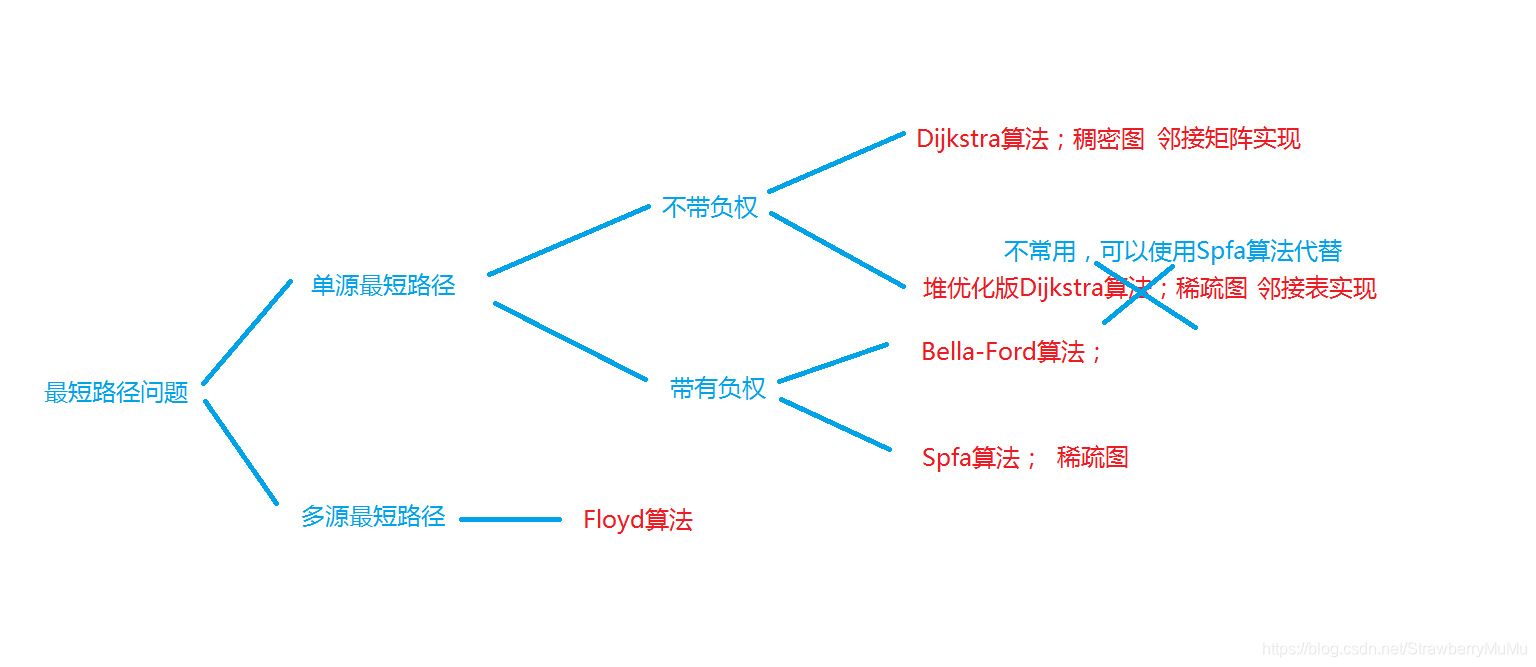
稠密图:Dijkstra算法;时间复杂度O(n^2)
稀疏图或者负权:Spfa算法;时间复杂度O(nm)
有步数限制的情况:Bella-Ford算法;时间复杂度O(nm)
多源组电路问题:Floyd算法;时间复杂度O(n^3)
最小生成树问题
邻接矩阵:Prim算法;时间复杂度O(n^2) 类似于Dijkstra算法
Kruskal算法;时间复杂度O(mlogm); 小根堆+并查集
 本文深入探讨了图算法中关键的几种方法,包括适用于稠密图的Dijkstra算法、适合稀疏图或存在负权边的SPFA算法、考虑步数限制的Bellman-Ford算法、多源组电路问题的Floyd算法,以及最小生成树问题的Prim和Kruskal算法。这些算法不仅涵盖了图论中的经典问题,还提供了高效解决实际问题的策略。
本文深入探讨了图算法中关键的几种方法,包括适用于稠密图的Dijkstra算法、适合稀疏图或存在负权边的SPFA算法、考虑步数限制的Bellman-Ford算法、多源组电路问题的Floyd算法,以及最小生成树问题的Prim和Kruskal算法。这些算法不仅涵盖了图论中的经典问题,还提供了高效解决实际问题的策略。
最短路问题

稠密图:Dijkstra算法;时间复杂度O(n^2)
稀疏图或者负权:Spfa算法;时间复杂度O(nm)
有步数限制的情况:Bella-Ford算法;时间复杂度O(nm)
多源组电路问题:Floyd算法;时间复杂度O(n^3)
最小生成树问题
邻接矩阵:Prim算法;时间复杂度O(n^2) 类似于Dijkstra算法
Kruskal算法;时间复杂度O(mlogm); 小根堆+并查集
 1833
1833
 224
224
 600
600
 433
433

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


