一、DFS与BFS
二、树与图的遍历：拓扑排序
三、最短路径
四、最小生成树
五、二分图：染色法、匈牙利算法
一、DFS与BFS
（一）DFS（深度优先遍历）
1、使用栈（stack）实现。
2、DFS所需要的空间是树的高度h
3、搜索到某个节点不具有最短性
4、回溯：回溯的时候，一定要记得恢复现场
5、剪枝：提前判断某个分支一定不合法，直接剪掉该分支
例题：
842.排列数字
题目描述
给定一个整数n，将数字1~n排成—排，将会有很多种排列方法。
现在，请你按照字典序将所有的排列方法输出。
输入格式
共一行，包含一个整数n。
输出格式
按字典序输出所有排列方案，每个方案占一行。
数据范围
1 ≦ n ≦ 7
输入样式：
3
输出样式：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
模拟思路：
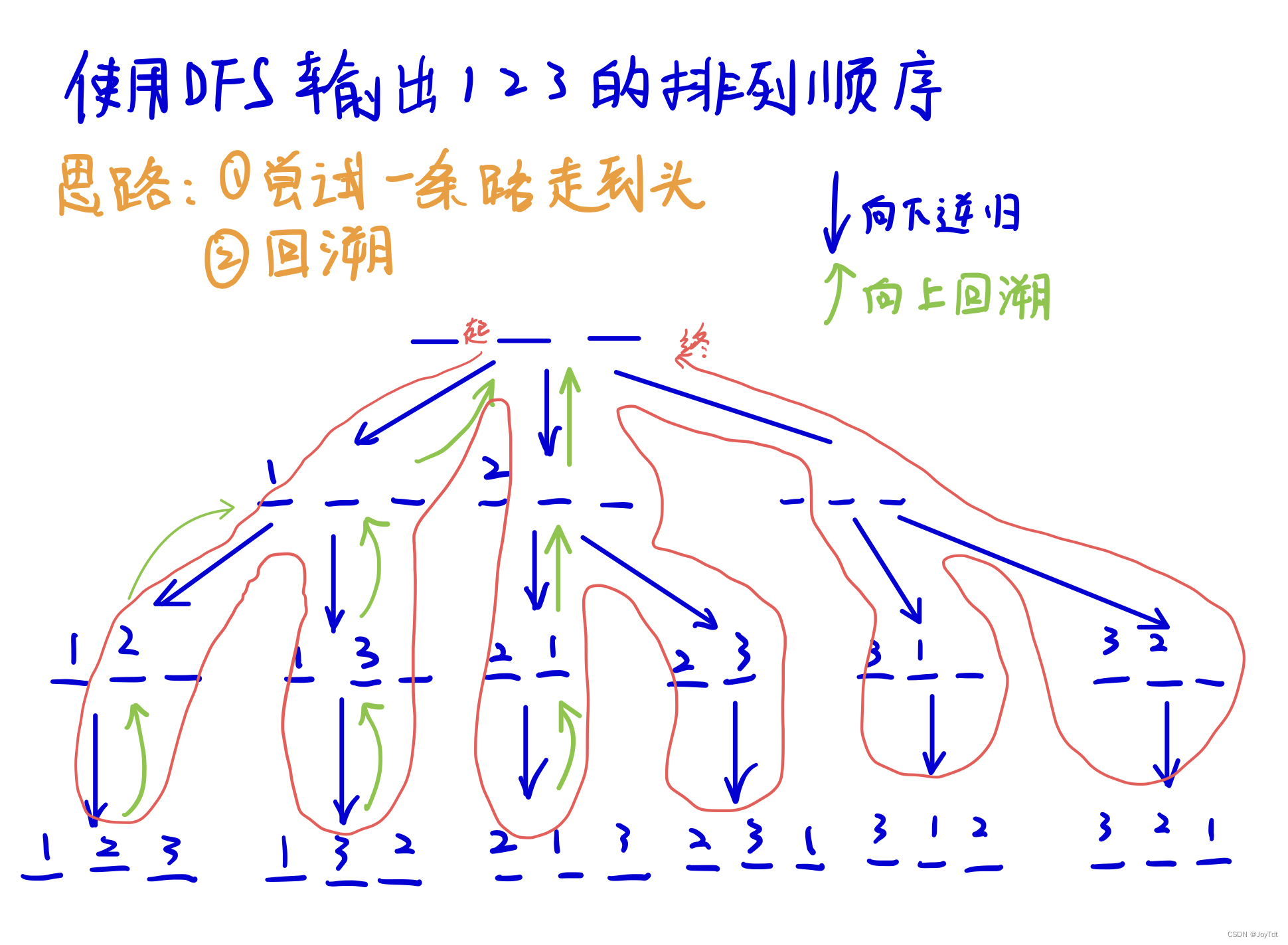
代码：
#include<bits/stdc++.h>
using namespace std;
const int N = 10;
int n;
int path[N]; // 记录所有的搜索路径
bool st[N]; // 记录这些点有没有被用过，true表示被用过，false表示没被使用
void dfs(int u) // 第u层
{
if(u == n) // 从0开始作为第一层，当搜索完最后一层，就输出这条路径并结束递归
{
for(int i = 0; i < n; i ++)
{
printf("%d ", path[i]);
}
puts("");
return;
}
for(int i = 1; i <= n; i ++)
{
if(!st[i]) // 如果i未被使用
{
path[u] = i; // 写入路径记录
st[i] = true; // 更新状态为已使用
dfs(u + 1); // 给下一层找数
//----------------------------------下一层递归结束，此时该恢复状态了
st[i] = false; // 更新状态为未使用
path[u] = 0; // 清空该层路径记录
}
}
}
int main()
{
cin>>n;
dfs(0);
return 0;
}
例题：
843.n-皇后问题
题目描述
n-皇后问题是指将n个皇后放在n*n的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。
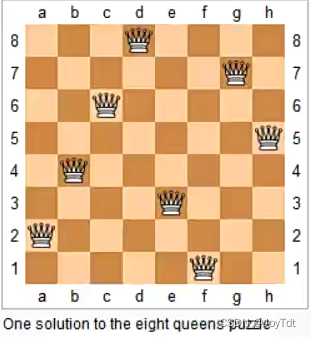
现在给定整数n，请你输出所有的满足条件的棋子摆法。
输入格式
共—行，包含整数n。
输出格式
每个解决方案占n行，每行输出一个长度为n的字符串，用来表示完整的棋盘状态。其中"."表示某一个位置的方格状态为空，"Q"表示某一个位置的方格上摆着皇后。每个方案输出完成后，输出一个空行。
数据范围
1 ≦ n ≦ 9
输入样式：
4
输出样式：
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
分析：
只要满足这一行，这一列，主对角线，和副对角线上没有被使用，就可以落子
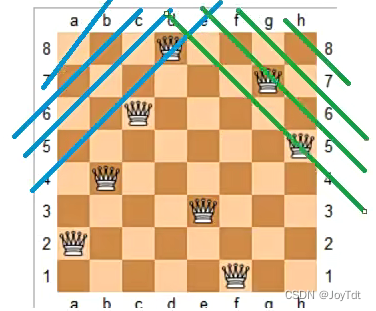
代码：
#include<bits/stdc++.h>
using namespace std;
const int N = 10;
int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N];
/*
只要满足这一行，这一列，主对角线，和副对角线上没有被使用，就可以落子。通过一定提炼后的做法。找到了规律（上方橙色字体）
*/
void dfs(int u) // 第u层
{
if(u == n) // 从0开始作为第一层，当搜索完最后一层，就输出这条路径并结束递归
{
for(int i = 0; i < n; i ++)
{
puts(g[i]);
}
puts("");
return;
}
for(int i = 0; i < n; i ++) // 在每个dfs中只处理这一行的情况
{
if(!col[i] && !dg[u + i] && !udg[n - u + i]) // 如果当前列，主对角线，副对角线都没有被占用
{
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true; // 更新状态为已使用
dfs(u + 1); // 给下一层找数
//----------------------------------下一层递归结束，此时该恢复状态了,进行回溯操作
col[i] = dg[u + i] = udg[n - u + i] = false; // 更新状态为未使用
g[u][i] = '.'; // 清空该层路径记录
}
}
}
/*
从(x,y)坐标开始判断能否放皇后，去除不能放的
*/
void dfs2(int x, int y, int s) // (x, y)代表当前坐标，s是皇后个数
{
if(y == n) y = 0, x ++; // 列满
if(x == n) // 行满
{
if(s == n) // 皇后放置满
{
for (int i = 0; i < n; i++) puts(g[i]);
puts("");
}
return;
}
// 不放皇后
dfs2(x, y + 1, s);
// 放皇后
if( !row[x] && !col[y] && !dg[x + y] && !udg[x - y + n])
{
g[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true; // 更新状态为已使用
dfs2(x, y + 1, s + 1);
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false; // 更新状态为未使用
g[x][y] = '.';
}
}
int main()
{
cin>>n;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
g[i][j] = '.';
// dfs(0);
dfs2(0, 0, 0);
return 0;
}
（二）BFS（广度优先遍历）
1、使用队列（queue）实现。
2、BFS需要的空间是2h
3、搜索到某个节点一般是具有最短性的路径，通常来说，求“最短”的操作，都可以用BFS来做
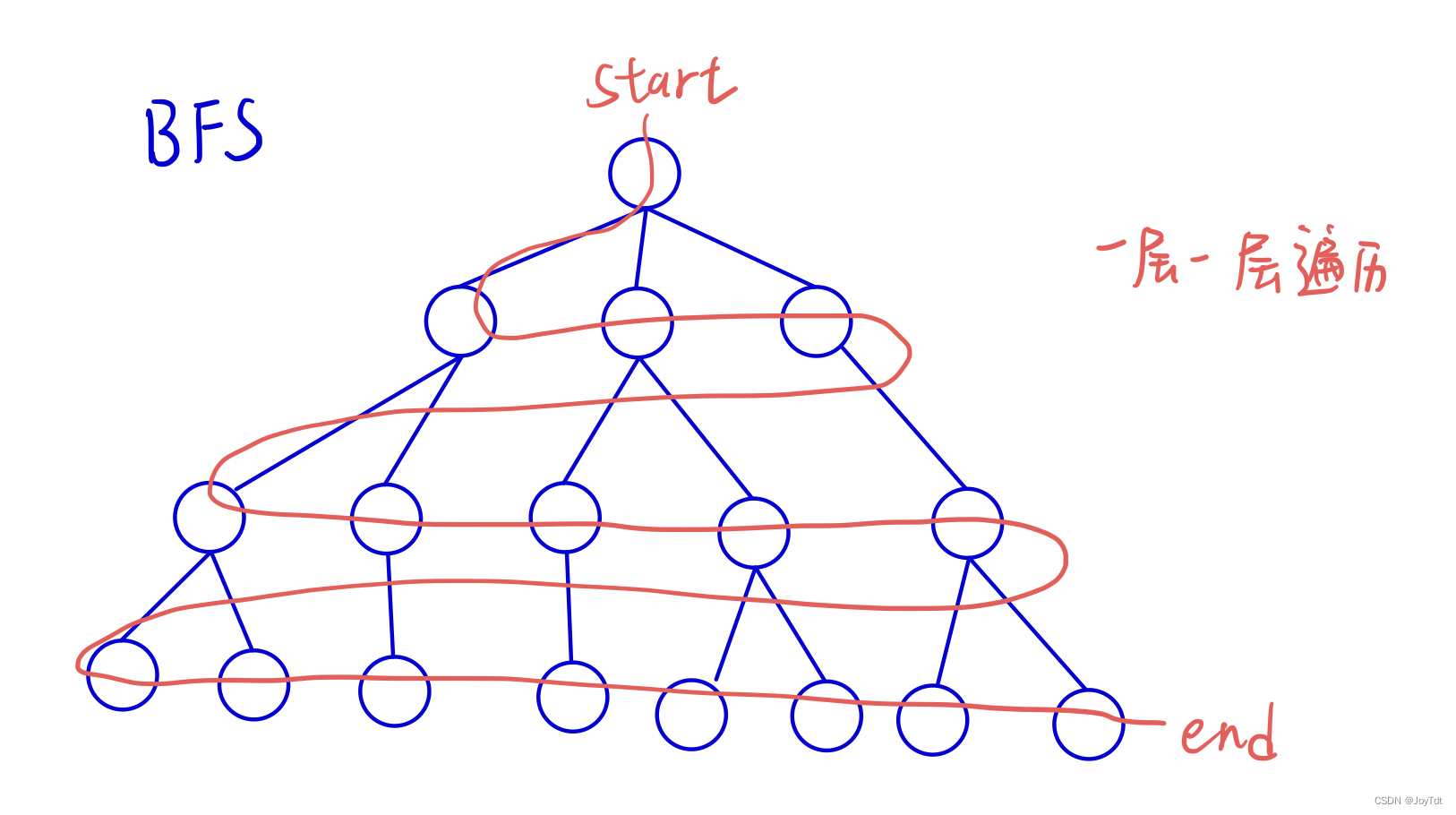
基本框架：
844.走迷宫
题目描述
给定一个n*m的二维整数数组，用来表示一个迷宫，数组中只包含0或1，其中0表示可以走的路，1表示不可通过的墙壁。
最初，有一个人位于左上角(1,1)处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。请问，该人从左上角移动至右下角(n, m)处，至少需要移动多少次。
数据保证(1,1)处和(n, m)处的数字为0，且一定至少存在一条通路。
输入格式
第—行包含两个整数n和m。
接下来n行，每行包含m个整数（(O或1)，表示完整的二维数组迷宫。
输出格式
输出路径。
输出一个整数，表示从左上角移动至右下角的最少移动次数。
数据范围
1 ≦ m ≦ n ≦ 100
输入样式：
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样式：
4 4
3 4
2 4
2 3
2 2
2 1
2 0
1 0
8
代码：
#include<bits/stdc++.h>
using namespace std;
const int N = 10;
typedef pair<int, int> PII; // 这里模拟队列
int n, m;
int g[N][N]; // 存放地图
int d[N][N]; // 存放到当前点已经走了几步了————————d[x][y] == -1代表这一点还有没有走到
PII q[N * N]; // 工作队列。存放当前路径经过的各个点的坐标{x, y}
PII Prev[N][N]; // 存放当前节点从哪里来的，即上一个节点是谁
int bfs()
{
// 初始化队列
int hh = 0, tt = 0;
q[0] = {
0, 0};
memset(d, -1, sizeof d); // 初始化d数组，全部置为-1
d[0][0] = 0;
int dx[4] = {
-1, 0, 1, 0}, dy[4] = {
0, 1, 0, -1}; // (dx[i], dy[i]) 就代表了，在当前这个节点往上下左右移动之后的位移矢量，分别为向上是(0，-1)，向右是(1, 0)，其他方向类似
while (hh <= tt) // 队列不为空
{
auto t = q[hh ++]; // bfs核心，拿队列中现存的节点
for(int i = 0; i < 4; i++) // 每个点接下来一共有四种走法，上下左右
{
int x = t.first + dx[i], y = t.second + dy[i]; // x,y对应新的移动后的点的坐标
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) // 新走的(x, y)满足边界内，且可以走这一点(g[x][y] == 0)，而且这一点未被走到过(d[x][y] == -1)
{
d[x][y
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
