强化学习（三）：时序差分学习（Temporal-Difference Learning, TD）

1. TD预测

TD是另一种对最优策略的学习方法，本节讲述TD预测，即使用TD求解策略$\pi$的值函数$v_{\pi }(s)$。

TD预测被称为 DP 和 MC 的结合体，DP是 期望更新+自举bootstrap，MC是 采样更新 + 样本估计。而TD则是采样更新 + 自举，即值函数$V(S_t)$更新基于采样得到的$V(S_{t+i})$的结果。

如果$i=1$，就为TD(0)单步TD算法，否则就为多步TD

当然动态特性$p(s^{\prime },a|s,a)$对于TD也是未知的。

1.1. TD(0)算法

根据采样更新与自举的思想，TD(0)的状态值函数预测式为

$$V(S_t)=V(S_t)+\alpha [R_{t+1}+\gamma V(S_{t+1})-V(S_t)]\text{\hspace{1em}(1)}$$

先给出一些定义：
TD目标：指$R_{t+1}+\gamma V(S_{t+1})$
TD误差：指$R_{t+1}+\gamma V(S_{t+1})-V(S_t)$
步长\学习率：指$\alpha$

如何理解上述定义呢？

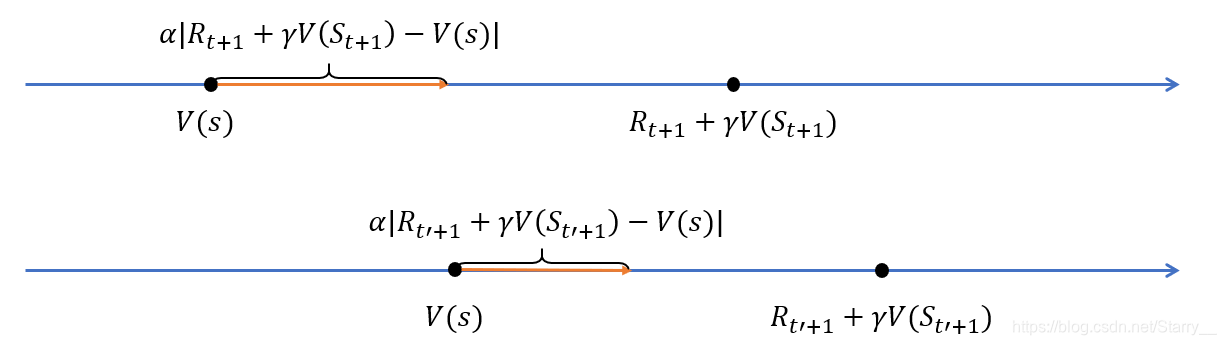
结合图一看就明白了。对于状态$s$，所有包含$s$的episode均会使值函数的估计值$V(s)$朝着TD目标走长度为 $\alpha$倍TD误差 的一步，而获得新的$V(s)$。就是经过这样不断地走，最终会接近$v_{\pi }(s)$。

有没有想到梯度下降中的步长的概念？意思其实是一样的，同样的可以使用非恒定学习率，例如$s的更$