作用
辗转相除法用于求得两个数之间的最小公约数,本文主要论证辗转相除法中的一个变换过程的数学逻辑合理性
前导声明
d
=
(
a
,
b
)
d = (a,b)
d=(a,b)表示
d
d
d是a、b的最大公约数
d
∣
a
d \vert a
d∣a表示
d
d
d整除a,即
a
m
o
d
d
=
=
0
a \bmod d == 0
amodd==0
a
=
b
∗
k
+
r
⇒
r
=
a
−
b
∗
k
a = b * k +r \Rightarrow r = a - b * k
a=b∗k+r⇒r=a−b∗k,其中,r即为a / b的余数,k即为a / b 的商
方法解析
方法1 ----夹逼法
令
d
0
=
(
a
,
b
)
d_0 = (a,b)
d0=(a,b),
d
1
=
(
r
,
b
)
d_1 = (r,b)
d1=(r,b)
则有
d
0
=
(
a
,
b
)
⟹
d
0
∣
a
∧
d
0
∣
b
d_0 = (a,b) \Longrightarrow d_0 \vert a \land d_0 \vert b
d0=(a,b)⟹d0∣a∧d0∣b
此时,由于有
r
=
a
−
b
∗
k
r = a - b * k
r=a−b∗k ,易证
d
0
∣
r
d_0 \vert r
d0∣r
因此,
d
0
d_0
d0是r、b的公因子,即
d
0
∣
(
b
,
r
)
=
d
1
⟹
d
0
<
=
d
1
d_0 \vert (b,r) = d_1 \Longrightarrow d_0 <= d_1
d0∣(b,r)=d1⟹d0<=d1
with the same reason,using
a
=
b
∗
k
+
r
a = b * k +r
a=b∗k+r and
d
1
=
(
r
,
b
)
d_1 = (r,b)
d1=(r,b) , we can conclude that
d
1
∣
(
b
,
r
)
=
d
0
⟹
d
1
<
=
d
0
d_1 \vert (b,r) = d_0 \Longrightarrow d_1 <= d_0
d1∣(b,r)=d0⟹d1<=d0
totally,we can see that
d
1
=
=
d
0
d_1 == d_0
d1==d0
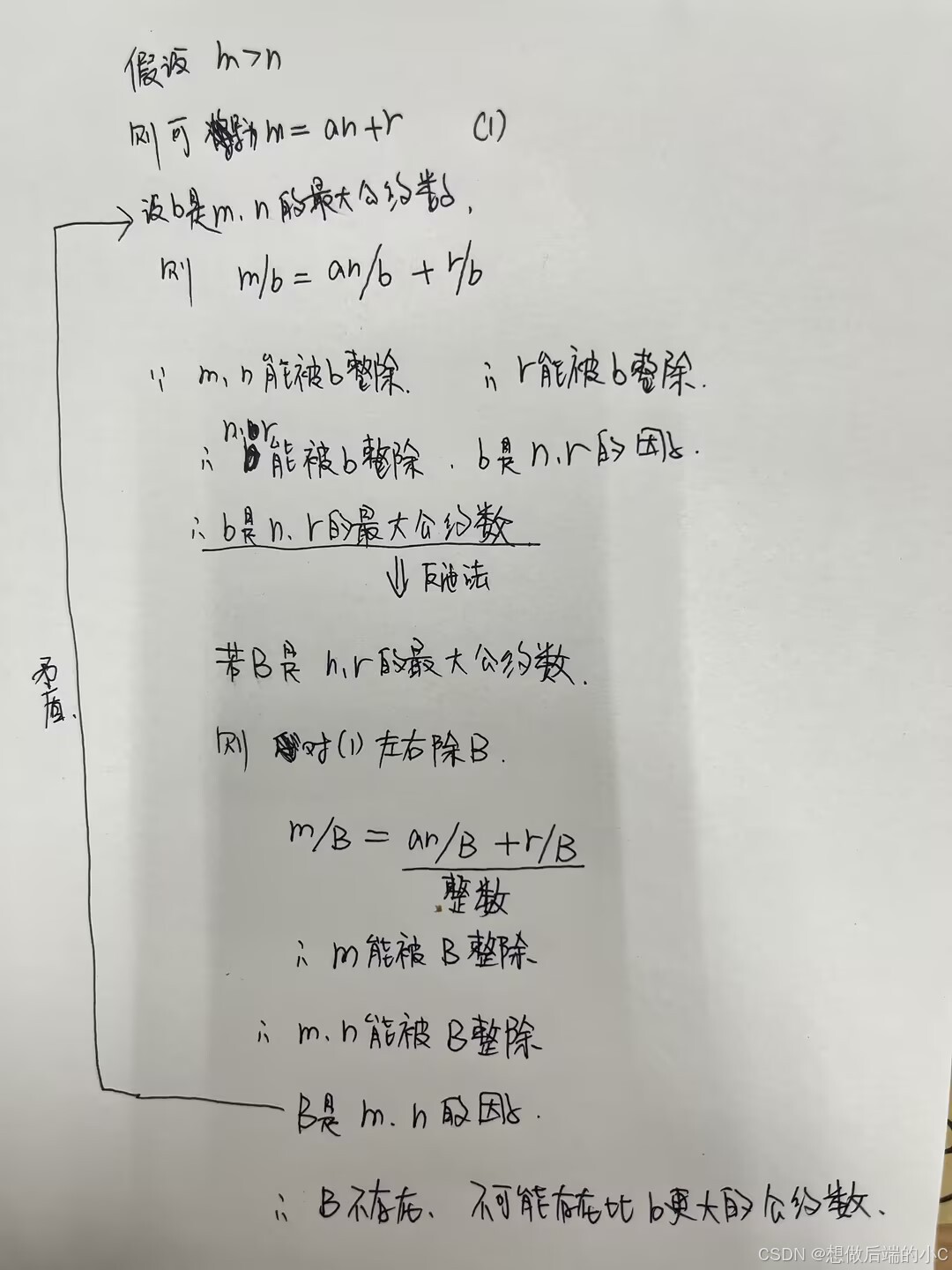
方法2 ----反证法
使用方法1得出的结论
d
0
d_0
d0是r、b的公因子
用反证法假设
d
1
=
(
b
,
r
)
d_1 = (b,r)
d1=(b,r),因此
d
1
>
d
0
d_1>d_0
d1>d0,同上理可得
d
1
d_1
d1也是a和b的公约数,可是这与
d
0
=
(
a
,
b
)
d_0 = (a,b)
d0=(a,b) 产生矛盾,故不存在
d
1
>
d
0
d_1>d_0
d1>d0,使得
d
0
=
(
a
,
b
)
d_0 = (a,b)
d0=(a,b) ,并且
d
1
=
(
b
,
r
)
d_1 = (b,r)
d1=(b,r)。因此
d
0
d_0
d0既等于
g
c
d
(
a
,
b
)
gcd(a,b)
gcd(a,b),又等于
g
c
d
(
b
,
r
)
gcd(b,r)
gcd(b,r),故得证。
























 4289
4289

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








