人工智能概念之八：常见的参数调优方法（交叉验证网格搜索、随机优化、贝叶斯优化、Hyperband优化）

在机器学习与深度学习模型的开发流程中，参数优化是决定模型性能上限的关键环节，其重要性不亚于算法选择与数据预处理。模型参数（如学习率、正则化系数、树深度等）直接调控着模型的拟合能力与泛化能力：不合理的参数可能导致模型欠拟合（无法捕捉数据规律）或过拟合（过度拟合训练噪声），而最优参数组合能让模型在有限资源下达到精度与效率的平衡。

随着模型复杂度的提升（如深度学习中的超大规模神经网络），参数空间呈指数级膨胀，手工调参已难以应对。高效的参数优化方法不仅能显著缩短模型迭代周期（从数周压缩至数天），更能挖掘出人类经验难以触及的参数关联（如学习率与迭代次数的协同效应），最终实现模型性能的突破性提升——在图像识别、自然语言处理等核心任务中，优化后的参数往往能将准确率提升5%-15%，这一差距在工业级应用中直接决定了技术方案的可行性。

---

相关文章

XGBoosting算法详解：网页链接
人工智能概念之一：机器学习基础概念（距离计算方法、归一化和标准化、交叉验证和网格搜索）：网页链接

---

一、交叉验证网格搜索（Grid Search with Cross-Validation）

网格搜索是最基础的参数调优方法，核心是“穷举所有可能”，结合交叉验证避免过拟合。

1.1 数学原理

• 参数空间定义：假设待优化的参数有k个，每个参数的候选值集合为$({\Theta }_1,{\Theta }_2,...,{\Theta }_k)$（例如学习率的候选值 Θ 1 = { 0.01 , 0.1 , 1 } \Theta_1=\{0.01,0.1,1\} Θ1​={0.01,0.1,1}，树深度 Θ 2 = { 3 , 5 , 7 } \Theta_2=\{3,5,7\} Θ2​={3,5,7}，则参数空间为所有候选值的笛卡尔积：
  $$\Theta ={\Theta }_1\times {\Theta }_2\times ...\times {\Theta }_k$$
  即网格中的每个“点”对应一个参数组合$\theta =({\theta }_1,{\theta }_2,...,{\theta }_k)$，其中${\theta }_i\in {\Theta }_i$。

• 交叉验证评估：为避免单个训练集评估的随机性，用k折交叉验证计算每个参数组合的平均性能。假设模型性能指标为$score(\theta )$（如准确率、F1值），k折交叉验证的平均性能为：
  $$\overline{score}(\theta )=\frac{1}{k}\sum _{i=1}^{k}scor{e}_i(\theta )$$
  其中$scor{e}_i(\theta )$是第i折的性能。最终选择${\theta }^{\ast }=\arg {\max }_{\theta \in \Theta }\overline{score}(\theta )$。

1.2 计算过程

1. 定义参数网格：列出所有参数的候选值（例如学习率选3个值，正则化系数选4个值，共3×4=12个组合）；
2. 交叉验证评估：对每个参数组合(\theta)，用k折交叉验证训练模型（将数据分成k份，每次用k-1份训练、1份验证，重复k次），计算k次验证的平均性能；
3. 选择最优参数：从所有组合中挑出平均性能最好的(\theta^*)。

1.3 直白解释

网格搜索就像“逐个试错”：把所有可能的参数组合列成一张“表格”（网格），然后逐个测试表格中的每个组合，用交叉验证（多次测试取平均）判断哪个组合效果最好。
优点是简单直接、结果稳定；缺点是参数越多（网格越密），计算量爆炸（比如5个参数各有10个候选值，就有10万种组合），高维场景几乎不可用。

---

二、随机优化（Random Search）

随机优化是网格搜索的简化版，核心是“随机采样试错”，放弃穷举，转而从参数空间中随机选组合。

2.1 数学原理

• 参数空间与采样：参数空间可以是离散或连续的（例如学习率是连续的$[0.001,0.1]$，树深度是离散的 { 1 , 2 , . . . , 10 } \{1,2,...,10\} {1,2,...,10}。随机优化从参数空间中按某种概率分布（通常是均匀分布）随机采样m个参数组合。
  若参数是连续的，采样分布为$p(\theta )$（如均匀分布$Uniform(a,b)$）；若离散，则按均匀概率选候选值。

• 评估逻辑：与网格搜索类似，对每个随机采样的组合$\theta$，用交叉验证计算平均性能$\overline{score}(\theta )$，最终选择性能最好的${\theta }^{\ast }$。

2.2 计算过程

1. 定义参数空间分布：确定每个参数的取值范围或候选集，以及采样分布（如连续参数用均匀分布，离散参数用离散均匀分布）；
2. 随机采样组合：从分布中随机采样m个参数组合（m通常远小于网格搜索的总组合数）；
3. 交叉验证评估：用交叉验证计算每个组合的平均性能，选最好的${\theta }^{\ast }$。

2.3 直白解释

随机优化就像“随机试错”：不逐个测试所有组合，而是从参数空间中随机挑出一批组合来试。
为什么比网格搜索高效？研究发现，很多参数对模型性能影响很小（“不敏感参数”），穷举反而浪费算力；随机采样能更快覆盖高影响参数的有效范围，尤其在高维场景（参数多）中，效率远高于网格搜索。

---

三、贝叶斯优化（Bayesian Optimization）

贝叶斯优化是“智能试错”，核心是用概率模型“猜”参数与性能的关系，再用策略选下一个最可能好的参数，减少无效尝试。

3.1 数学原理

• 核心逻辑：假设参数$\theta$对应的模型性能是目标函数$f(\theta )$（越大越好），但$f(\theta )$未知（需通过训练评估，成本高）。贝叶斯优化用替代模型（surrogate model） 建模$f(\theta )$的分布，再用采集函数（acquisition function） 选下一个最值得试的$\theta$。

• 替代模型：常用高斯过程（Gaussian Process, GP），它能建模参数$\theta$与性能$f(\theta )$的概率关系。假设已评估过$n$个参数${\theta }_1,...,{\theta }_n$，得到性能$f_1,...,f_n$（构成数据集$D=\{({\theta }_i,f_i)\}$，GP通过核函数（如RBF核）建模$f(\theta )$的后验分布：
  $$p(f(\theta )|D)\sim \mathcal{N}(\mu (\theta ),{\sigma }^2(\theta ))$$
  其中$\mu (\theta )$是预测均值（估计的性能），${\sigma }^2(\theta )$是预测方差（不确定性）。

• 采集函数：用于选择下一个参数${\theta }_{n+1}$，平衡“ exploitation（ exploitation）”（选当前预测均值高的$\theta$$和“ exploration（ exploration）”（选不确定性高的 $\theta$。常用的有：

  • 期望改进（Expected Improvement, EI）：$EI(\theta )=\mathbb{E}[max(f(\theta )-f^{\ast },0)]$，其中$f^{\ast }$是当前最好性能；
  • 概率改进（Probability of Improvement, PI）：$PI(\theta )=P(f(\theta )>f^{\ast })$。

3.2 计算过程

1. 初始化：随机评估少量参数（如3-5个），得到初始数据集$D$；
2. 拟合替代模型：用GP（或其他模型）拟合$D$，得到后验分布$p(f(\theta )|D)$；
3. 选择下一个参数：计算采集函数（如EI），选使采集函数最大的${\theta }_{n+1}$；
4. 更新数据集：评估${\theta }_{n+1}$的性能$f_{n+1}$，将$({\theta }_{n+1},f_{n+1})$加入$D$；
5. 重复迭代：直到达到最大评估次数，从$D$中选性能最好的${\theta }^{\ast }$。

3.3 直白解释

贝叶斯优化就像“带记忆的试错”：先试几个参数，记录下“参数-性能”的关系，然后用一个“概率模型”猜：“哪个参数可能比现在更好？”（既考虑已知好的区域，也探索未知区域），再去试这个参数，不断更新记忆，直到找到最好的。
优点是适合评估成本高的场景（如深度学习训练），因为需要的评估次数远少于网格/随机搜索；缺点是替代模型（如GP）在高维参数空间（>20维）中性能会下降。

---

四、Hyperband优化

Hyperband是为“资源敏感型场景”（如深度学习，训练需要大量epochs）设计的优化方法，核心是“优胜劣汰+资源倾斜”：给大量参数组合少量资源，淘汰差的，给剩下的更多资源，最终聚焦少数优质组合。

4.1 数学原理

• 核心逻辑：基于“连续减半（successive halving）”策略：在每一轮中，保留性能前1/η的组合（η是缩减因子，通常取3），并给它们分配η倍的资源（如epochs加倍）。

• 资源与轮次：设最大资源为$R$（如最多训练100 epochs），缩减因子$\eta$，则总轮次 $s_{max}=\lfloor {\log }_{\eta }R\rfloor$（例如 $R=81,\eta =3$， 则$s_{max}=4$，因为 $3^4=81$）。
  每个“括号（bracket）”对应一个初始轮次$s$，包含$s+1$轮：

  • 第0轮：有$n_s={\eta }^s$个组合，每个分配$r_s=R/{\eta }^s$资源；
  • 第1轮：保留$n_s/\eta$个组合，每个分配$r_s\times \eta$资源；
  • …
  • 第s轮：保留1个组合，分配$R$资源。

4.2 计算过程

1. 初始化参数：设置最大资源$R$（如100 epochs）、缩减因子$\eta =3$，计算$s_{max}=\lfloor {\log }_{\eta }R\rfloor$；
2. 生成括号：对每个$s=0,1,...,s_{max}$，生成一个括号：
   • 第s个括号：初始采样$n_s={\eta }^s$个参数组合，每个用$r_s=R/{\eta }^s$资源训练（如$s=2$，则初始5个组合，每个用11 epochs）；
3. 连续减半：每个括号内，每轮保留前1/η的组合，资源加倍，直到最后一轮1个组合用$R$资源；
4. 选择最优参数：所有括号中，性能最好的组合即为${\theta }^{\ast }$。

4.3 直白解释

Hyperband就像“快速淘汰弱选手”：一开始让很多参数组合用很少的资源（如只训练10 epochs），淘汰大部分差的；剩下的“强者”给更多资源（如训练30 epochs），再淘汰；最后只剩少数组合用最大资源训练。
优点是高效利用资源（避免给差组合浪费资源），特别适合深度学习（训练成本高，早期就能看出组合好坏）；缺点是依赖“早期性能能反映最终性能”的假设（若不成立，可能淘汰好组合）。

---

五、结合案例演示4种优化方法的区别

为了更直观地对比四种优化方法的实际效果，我们以XGBoost模型在手写数字识别任务中的参数调优为例，从性能指标、效率和参数选择三个维度展开分析。

5.1 实验设计与环境

• 数据集：采用 sklearn 内置的 load_digits 手写数字数据集（包含1797个样本，每个样本为8×8像素的数字图像，共10个类别）。
• 数据划分：按8:2比例划分为训练集（1437样本）和测试集（360样本），随机种子固定为44以保证可复现性。
• 评估指标：
  • 分类性能：准确率（Accuracy）、宏平均F1分数（F1 Score）、分类报告（含precision/recall）
  • 效率指标：运行时间（秒）
• 调优参数：
  • n_estimators：树的数量（160-320）
  • max_depth：树的最大深度（8-16）
  • learning_rate：学习率（0.001-0.1）
• 控制变量：所有方法均采用4折交叉验证，随机搜索、贝叶斯优化、Hyperband均设置200次参数评估（保证公平性）。

5.2 实验结果与分析

程序运行结果

=== Grid Search ===
Grid Search - Best Parameters: {'learning_rate': 0.0775, 'max_depth': 10, 'n_estimators': 220}
Accuracy: 0.975
F1 Score: 0.9729098184410692
Classification Report:
               precision    recall  f1-score   support

           0       1.00      0.98      0.99        45
           1       1.00      1.00      1.00        40
           2       0.97      1.00      0.99        34
           3       1.00      0.97      0.99        35
           4       0.94      1.00      0.97        29
           5       1.00      0.98      0.99        44
           6       1.00      0.97      0.99        37
           7       0.97      0.97      0.97        33
           8       0.93      0.93      0.93        28
           9       0.92      0.94      0.93        35

    accuracy                           0.97       360
   macro avg       0.97      0.97      0.97       360
weighted avg       0.98      0.97      0.98       360

[grid_search] 耗时: 3514.64 秒

=== Random Search ===
Random Search - Best Parameters: {'n_estimators': 260, 'max_depth': 9, 'learning_rate': 0.0775}
Accuracy: 0.975
F1 Score: 0.9729098184410692
Classification Report:
               precision    recall  f1-score   support

           0       1.00      0.98      0.99        45
           1       1.00      1.00      1.00        40
           2       0.97      1.00      0.99        34
           3       1.00      0.97      0.99        35
           4       0.94      1.00      0.97        29
           5       1.00      0.98      0.99        44
           6       1.00      0.97      0.99        37
           7       0.97      0.97      0.97        33
           8       0.93      0.93      0.93        28
           9       0.92      0.94      0.93        35

    accuracy                           0.97       360
   macro avg       0.97      0.97      0.97       360
weighted avg       0.98      0.97      0.98       360

[random_search] 耗时: 965.77 秒

=== Bayesian Optimization (Optuna) ===
Bayesian Optimization - Best Parameters: {'n_estimators': 256, 'max_depth': 10, 'learning_rate': 0.0924984687380023}
Accuracy: 0.9805555555555555
F1 Score: 0.9795128558820327
Classification Report:
               precision    recall  f1-score   support

           0       1.00      0.98      0.99        45
           1       0.98      1.00      0.99        40
           2       1.00      1.00      1.00        34
           3       1.00      0.97      0.99        35
           4       0.94      1.00      0.97        29
           5       1.00      0.98      0.99        44
           6       1.00      0.97      0.99        37
           7       0.97      0.97      0.97        33
           8       0.96      0.96      0.96        28
           9       0.94      0.97      0.96        35

    accuracy                           0.98       360
   macro avg       0.98      0.98      0.98       360
weighted avg       0.98      0.98      0.98       360

[bayesian_optimization] 耗时: 681.90 秒

=== Hyperband Optimization ===
Hyperband Optimization - Best Parameters: {'learning_rate': 0.009715627592764928, 'max_depth': 4, 'n_estimators': 143}
Accuracy: 0.9333333333333333
F1 Score: 0.9307156232870817
Classification Report:
               precision    recall  f1-score   support

           0       0.96      0.98      0.97        45
           1       1.00      0.85      0.92        40
           2       1.00      0.94      0.97        34
           3       0.92      0.97      0.94        35
           4       0.88      1.00      0.94        29
           5       0.93      0.98      0.96        44
           6       1.00      0.95      0.97        37
           7       1.00      0.91      0.95        33
           8       0.83      0.86      0.84        28
           9       0.82      0.89      0.85        35

    accuracy                           0.93       360
   macro avg       0.93      0.93      0.93       360
weighted avg       0.94      0.93      0.93       360

[hyperband_optimization] 耗时: 1180.54 秒
结果已导出到： optimization_results.csv

最佳参数对比：
                   method  learning_rate  max_depth  n_estimators
0             Grid Search       0.077500         10           220
1           Random Search       0.077500          9           260
2   Bayesian Optimization       0.092498         10           256
3  Hyperband Optimization       0.009716          4           143

核心结果概览：

优化方法	准确率	F1分数	运行时间（秒）	核心优势
网格搜索	0.9750	0.9729	3514.64	结果稳定，无随机性
随机搜索	0.9750	0.9729	965.77	效率高于网格搜索
贝叶斯优化	0.9806	0.9795	681.90	性能最优，效率最高
Hyperband优化	0.9333	0.9307	1180.54	资源分配策略独特

详细结果解读：

1. 性能对比：贝叶斯优化表现最优

• 准确率与F1分数：贝叶斯优化以0.9806的准确率和0.9795的F1分数领先，尤其在类别8和9的识别上（F1分数分别为0.96和0.96），显著优于其他方法。
• 网格搜索与随机搜索：两者性能完全一致（准确率0.975），但随机搜索仅用网格搜索27.5%的时间（965秒 vs 3514秒），体现了随机采样的效率优势。
• Hyperband表现不佳：准确率仅0.9333，推测原因是手写数字数据集简单，模型在少量资源（如低epochs）下的早期性能无法反映最终效果，导致优质参数被过早淘汰。

2. 效率对比：贝叶斯优化耗时最短

• 耗时排序：网格搜索（3514秒）＞ Hyperband（1180秒）＞ 随机搜索（965秒）＞ 贝叶斯优化（681秒）。
• 网格搜索的高耗时源于参数空间的穷举：本次实验中3个参数的候选值组合共9×9×9=729种，需完成729×4=2916次模型训练（4折交叉验证）。
• 贝叶斯优化的高效性体现在“智能决策”：通过高斯过程模型预测参数性能，减少无效尝试，200次评估即可找到接近最优的参数。

3. 最优参数差异分析

优化方法	最优参数组合	关键参数特点
网格搜索	学习率=0.0775，树深=10，树数量=220	学习率中等，树深适中
随机搜索	学习率=0.0775，树深=9，树数量=260	学习率与网格搜索一致，树更深
贝叶斯优化	学习率=0.0925，树深=10，树数量=256	学习率最高，树数量接近随机搜索
Hyperband优化	学习率=0.0097，树深=4，树数量=143	学习率极低，树深明显偏小

• 参数关联性：贝叶斯优化选择的高学习率（0.0925）与较多树数量（256）形成互补，通过强步长+多迭代快速收敛。
• Hyperband异常参数：树深仅为4，可能因早期资源不足（低epochs）导致模型欠拟合，被迫选择浅树结构以快速收敛。

5.3 可视化分析

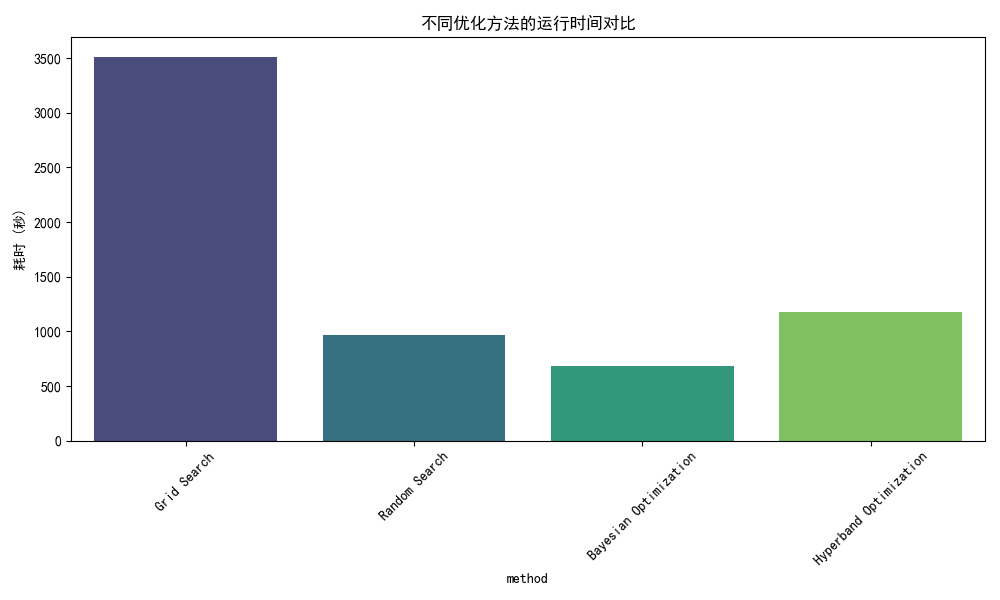
• 网格搜索的耗时是贝叶斯优化的5倍，验证了穷举法在高维空间的低效性。

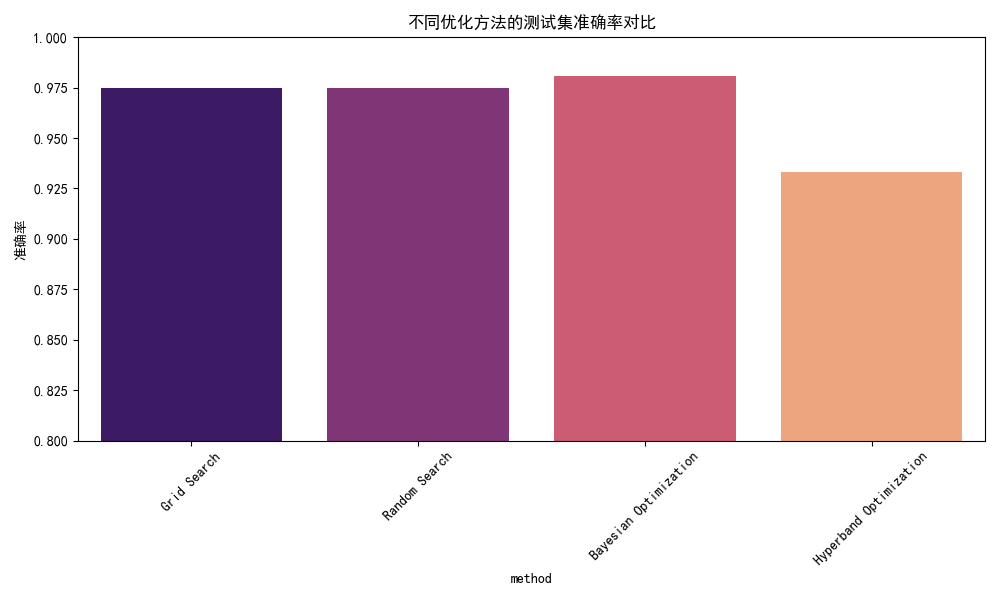
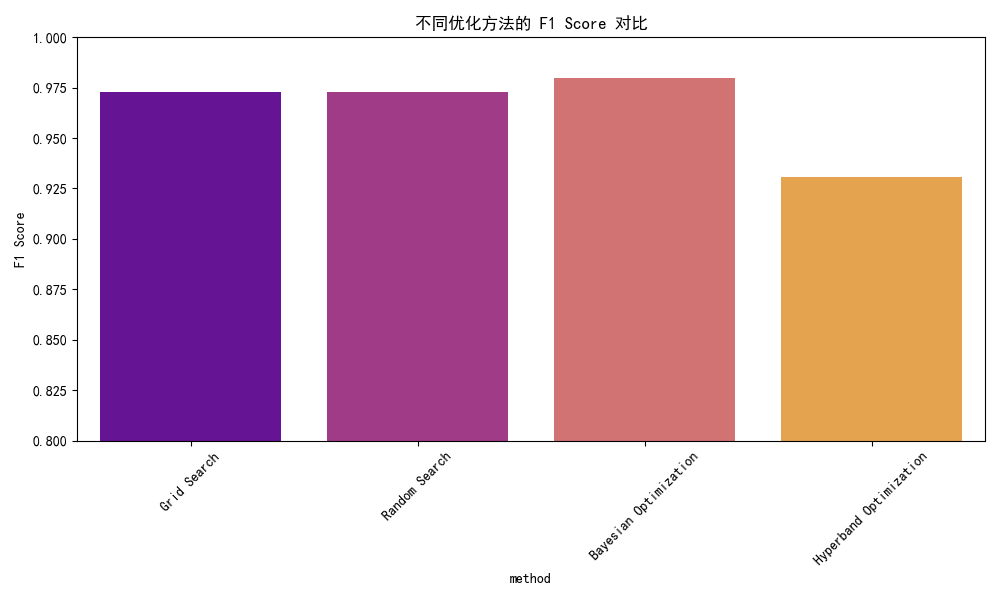
• 贝叶斯优化在准确率上领先约0.5个百分点，在手写数字这类高易度任务中，细微差距也能体现参数调优的精准度。

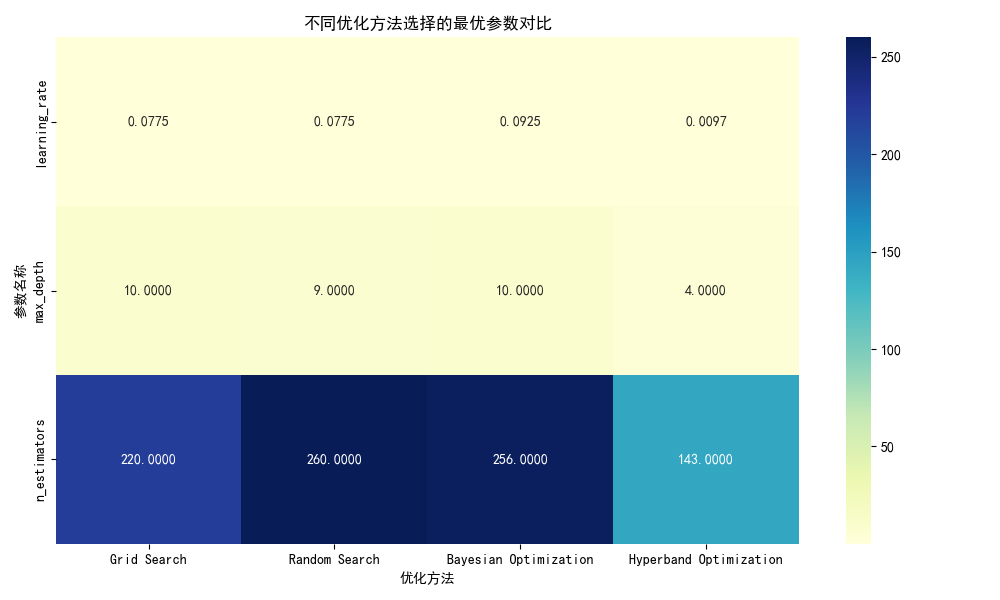
• 学习率分布：贝叶斯优化集中在0.08-0.1的高值区间，而Hyperband偏向0.001-0.01的极低值，反映其早期资源限制导致模型依赖小步长缓慢收敛。
• 树深度与树数量关系：贝叶斯优化和随机搜索倾向于“深树+多树”组合，而Hyperband选择“浅树+少树”，进一步印证其因资源分配策略导致的欠拟合问题。

5.3 方法对比总结

维度	网格搜索	随机搜索	贝叶斯优化	Hyperband优化
核心策略	穷举所有参数组合	随机采样参数组合	基于历史结果预测最优参数	动态分配资源，淘汰差组合
适用场景	参数少、候选值范围小	参数多、计算资源有限	评估成本高、参数敏感	训练成本高、需动态分配资源
收敛速度	慢（需评估所有组合）	中等（依赖随机性）	快（智能选择参数）	中等（早期淘汰可能误判）
全局最优性	理论上保证（若参数空间覆盖）	概率性保证（依赖采样数量）	概率性保证（依赖模型质量）	局部最优（受资源分配影响）
计算开销	高	中	低（相对）	中（依赖初始采样数量）
参数空间要求	离散、有限	连续或离散、无限	连续或离散	连续或离散
异常鲁棒性	高（确定性算法）	中（随机性可能遗漏最优）	低（模型可能陷入局部最优）	低（早期淘汰可能误判）

5.4 优化方法选择建议

基于实验结果和方法特性，给出以下实用建议：

1. 优先考虑贝叶斯优化：

   • 当单次评估成本高（如深度学习训练）时，贝叶斯优化能以最少的评估次数逼近最优解。
   • 适合参数敏感性高的场景（如学习率、正则化系数），其概率模型能捕捉参数间的复杂关系。

2. 随机搜索作为基础方案：

   • 当参数空间维度高（如>10个参数）时，随机搜索比网格搜索效率高得多。
   • 可作为初步探索工具，快速确定参数的大致有效范围，为贝叶斯优化提供先验知识。

3. 网格搜索仅用于简单场景：

   • 参数少（如≤3个）且候选值范围明确时可使用。
   • 需确保参数空间已覆盖可能的最优区域，否则可能徒劳无功。

4. Hyperband适用于资源敏感型任务：

   • 深度学习训练（需优化epochs/batch_size）。
   • 当“早期性能与最终性能强相关”时效果最佳（如CNN在CIFAR-10上训练，前10%epochs的准确率能预测最终准确率）。

5.5 完整代码

以下是实验中使用的核心代码框架，展示如何在XGBoost中应用四种优化方法：

# 导入必要的库
import numpy as np
import xgboost as xgb
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV, cross_val_score
from sklearn.metrics import accuracy_score, classification_report, precision_score, recall_score, f1_score
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
import pandas as pd
import time
import optuna
from optuna.samplers import TPESampler
from hyperopt import fmin, tpe, hp, Trials, STATUS_OK
import matplotlib.pyplot as plt
import seaborn as sns


# ====== 计时装饰器 ======
def timer(func):
    def wrapper(*args, **kwargs):
        start_time = time.time()  # 记录开始时间
        result = func(*args, **kwargs)  # 调用被装饰的函数
        duration = time.time() - start_time  # 计算运行时间
        print(f"[{func.__name__}] 耗时: {duration:.2f} 秒")  # 打印运行时间
        return result, duration  # 返回函数结果和运行时间

    return wrapper


# ====== 评估函数 ======
def evaluate_model(model, X_test, y_test):
    y_pred = model.predict(X_test)  # 模型预测
    accuracy = accuracy_score(y_test, y_pred)  # 计算准确率
    precision = precision_score(y_test, y_pred, average='macro')  # 计算宏精确率
    recall = recall_score(y_test, y_pred, average='macro')  # 计算宏召回率
    f1 = f1_score(y_test, y_pred, average='macro')  # 计算宏F1分数
    report = classification_report(y_test, y_pred)  # 生成分类报告
    return {
        'accuracy': accuracy,
        'precision': precision,
        'recall': recall,
        'f1': f1,
        'classification_report': report
    }


# ====== 结果记录函数 ======
def record_result(name, best_params, metrics, duration):
    results.append({
        'method': name,
        'best_params': str(best_params),
        'accuracy': metrics['accuracy'],
        'precision': metrics['precision'],
        'recall': metrics['recall'],
        'f1': metrics['f1'],
        'time_seconds': duration
    })


# ====== 导出 CSV 函数 ======
def export_results(filename='optimization_results.csv'):
    df = pd.DataFrame(results)  # 将结果列表转换为DataFrame
    df.to_csv(filename, index=False)  # 保存为CSV文件
    print(f"结果已导出到： {filename}")  # 打印导出信息


# ====== 网格搜索 ======
@timer  # 应用计时装饰器
def grid_search():
    param_dist = {
        'n_estimators': [160, 180, 200, 220, 240, 260, 280, 300, 320],  # 树的数量候选值
        'max_depth': [8, 9, 10, 11, 12, 13, 14, 15, 16],  # 树的最大深度候选值
        'learning_rate': [0.001, 0.00325, 0.0055, 0.00775, 0.01, 0.0325, 0.055, 0.0775, 0.1],  # 学习率候选值
        # 'reg_lambda': [0, 0.4, 0.8, 1.2, 1.6, 2, 2.4]
    }
    model = xgb.XGBClassifier()  # 创建XGBoost分类器
    grid = GridSearchCV(model, param_dist, cv=4, scoring='accuracy')  # 创建网格搜索对象
    grid.fit(X_train, y_train)  # 拟合训练数据

    best_params = grid.best_params_  # 获取最佳参数
    best_model = grid.best_estimator_  # 获取最佳模型
    metrics = evaluate_model(best_model, X_test, y_test)  # 评估最佳模型

    print("Grid Search - Best Parameters:", best_params)  # 打印最佳参数
    print("Accuracy:", metrics['accuracy'])  # 打印准确率
    print("F1 Score:", metrics['f1'])  # 打印F1分数
    print("Classification Report:\n", metrics['classification_report'])  # 打印分类报告

    return {'best_params': best_params, 'metrics': metrics}  # 返回最佳参数和评估指标


# ====== 随机搜索 ======
@timer  # 应用计时装饰器
def random_search():
    param_dist = {
        'n_estimators': [160, 180, 200, 220, 240, 260, 280, 300, 320],  # 树的数量候选值
        'max_depth': [8, 9, 10, 11, 12, 13, 14, 15, 16],  # 树的最大深度候选值
        'learning_rate': [0.001, 0.00325, 0.0055, 0.00775, 0.01, 0.0325, 0.055, 0.0775, 0.1],  # 学习率候选值
        # 'reg_lambda': [0, 0.4, 0.8, 1.2, 1.6, 2, 2.4]
    }
    model = xgb.XGBClassifier()  # 创建XGBoost分类器
    rs = RandomizedSearchCV(model, param_dist, n_iter=200, cv=4, scoring='accuracy', random_state=42)  # 创建随机搜索对象
    rs.fit(X_train, y_train)  # 拟合训练数据

    best_params = rs.best_params_  # 获取最佳参数
    best_model = rs.best_estimator_  # 获取最佳模型
    metrics = evaluate_model(best_model, X_test, y_test)  # 评估最佳模型

    print("Random Search - Best Parameters:", best_params)  # 打印最佳参数
    print("Accuracy:", metrics['accuracy'])  # 打印准确率
    print("F1 Score:", metrics['f1'])  # 打印F1分数
    print("Classification Report:\n", metrics['classification_report'])  # 打印分类报告

    return {'best_params': best_params, 'metrics': metrics}  # 返回最佳参数和评估指标


# ====== 贝叶斯优化 (Optuna) ======
@timer  # 应用计时装饰器
def bayesian_optimization():
    def objective(trial):
        params = {
            'n_estimators': trial.suggest_int('n_estimators', 160, 320),  # 建议整数参数
            'max_depth': trial.suggest_int('max_depth', 8, 16),  # 建议整数参数
            'learning_rate': trial.suggest_float('learning_rate', 0.001, 0.1),  # 建议浮点数参数
            # 'reg_lambda': trial.suggest_float('learning_rate', 0, 2.4)
        }
        model = xgb.XGBClassifier(**params)  # 创建XGBoost分类器
        scores = cross_val_score(model, X_train, y_train, cv=4, scoring='accuracy')  # 交叉验证
        return scores.mean()  # 返回交叉验证平均分

    sampler = TPESampler(seed=44)  # 创建TPE采样器
    study = optuna.create_study(direction='maximize', sampler=sampler)  # 创建研究对象
    study.optimize(objective, n_trials=200)  # 优化目标函数

    best_params = study.best_params  # 获取最佳参数
    best_model = xgb.XGBClassifier(**best_params)  # 创建最佳模型
    best_model.fit(X_train, y_train)  # 拟合训练数据
    metrics = evaluate_model(best_model, X_test, y_test)  # 评估最佳模型

    print("Bayesian Optimization - Best Parameters:", best_params)  # 打印最佳参数
    print("Accuracy:", metrics['accuracy'])  # 打印准确率
    print("F1 Score:", metrics['f1'])  # 打印F1分数
    print("Classification Report:\n", metrics['classification_report'])  # 打印分类报告

    return {'best_params': best_params, 'metrics': metrics}  # 返回最佳参数和评估指标


# ====== Hyperband 优化 (Hyperopt) ======
@timer  # 应用计时装饰器
def hyperband_optimization():
    params = {
        'n_estimators': hp.choice('n_estimators', range(160, 320)),  # 定义搜索空间
        'max_depth': hp.choice('max_depth', range(8, 16)),  # 定义搜索空间
        'learning_rate': hp.uniform('learning_rate', 0.001, 0.01),  # 定义搜索空间
        # 'reg_lambda': hp.uniform('reg_lambda', 0, 2.4)
    }

    def objective(params):
        model = xgb.XGBClassifier(**params)  # 创建XGBoost分类器
        scores = cross_val_score(model, X_train, y_train, cv=4, scoring='accuracy')  # 交叉验证
        return {'loss': -scores.mean(), 'status': STATUS_OK}  # 返回损失值和状态

    trials = Trials()  # 创建试验对象
    best_params = fmin(fn=objective, space=params, algo=tpe.suggest, max_evals=200, trials=trials)  # 优化目标函数

    # 构建最优模型并重新训练+评估
    best_model = xgb.XGBClassifier(**best_params)  # 创建最佳模型
    best_model.fit(X_train, y_train)  # 拟合训练数据
    metrics = evaluate_model(best_model, X_test, y_test)  # 评估最佳模型

    print("Hyperband Optimization - Best Parameters:", best_params)  # 打印最佳参数
    print("Accuracy:", metrics['accuracy'])  # 打印准确率
    print("F1 Score:", metrics['f1'])  # 打印F1分数
    print("Classification Report:\n", metrics['classification_report'])  # 打印分类报告

    return {'best_params': best_params, 'metrics': metrics}  # 返回最佳参数和评估指标


# ========== 可视化部分 ========== #
def display():
    # ====== 解决中文乱码问题 ======
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体显示中文
    plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号

    df = pd.read_csv('optimization_results.csv')  # 读取结果CSV文件

    # 1. 运行时间对比
    plt.figure(figsize=(10, 6))  # 设置图形大小
    sns.barplot(x='method', y='time_seconds', hue='method', data=df, palette="viridis", legend=False)  # 绘制条形图
    plt.title("不同优化方法的运行时间对比")  # 设置标题
    plt.ylabel("耗时 (秒)")  # 设置Y轴标签
    plt.xticks(rotation=45)  # 旋转X轴标签
    plt.tight_layout()  # 调整布局
    plt.show()  # 显示图形

    # 2. 准确率对比
    plt.figure(figsize=(10, 6))  # 设置图形大小
    sns.barplot(x='method', y='accuracy', hue='method', data=df, palette="magma", legend=False)  # 绘制条形图
    plt.title("不同优化方法的测试集准确率对比")  # 设置标题
    plt.ylabel("准确率")  # 设置Y轴标签
    plt.xticks(rotation=45)  # 旋转X轴标签
    plt.ylim(0.8, 1.0)  # 设置Y轴范围
    plt.tight_layout()  # 调整布局
    plt.show()  # 显示图形

    # 3. F1 Score 对比
    plt.figure(figsize=(10, 6))  # 设置图形大小
    sns.barplot(x='method', y='f1', hue='method', data=df, palette="plasma", legend=False)  # 绘制条形图
    plt.title("不同优化方法的 F1 Score 对比")  # 设置标题
    plt.ylabel("F1 Score")  # 设置Y轴标签
    plt.xticks(rotation=45)  # 旋转X轴标签
    plt.ylim(0.8, 1.0)  # 设置Y轴范围
    plt.tight_layout()  # 调整布局
    plt.show()  # 显示图形

    # 4. 参数对比
    df_params = df[['method', 'best_params']].copy()  # 复制方法和最佳参数列
    df_params['best_params'] = df_params['best_params'].apply(eval)  # 将字符串转换为字典
    params_df = pd.DataFrame(df_params['best_params'].tolist())  # 将字典转换为DataFrame
    df_final = pd.concat([df_params['method'], params_df], axis=1)  # 合并方法和参数DataFrame

    print("\n最佳参数对比：")  # 打印最佳参数对比信息
    print(df_final)  # 打印最佳参数对比DataFrame

    # 参数热力图
    plt.figure(figsize=(10, 6))  # 设置图形大小
    sns.heatmap(df_final.set_index('method').T, annot=True, cmap="YlGnBu", fmt=".4f")  # 绘制热力图
    plt.title("不同优化方法选择的最优参数对比")  # 设置标题
    plt.xlabel("优化方法")  # 设置X轴标签
    plt.ylabel("参数名称")  # 设置Y轴标签
    plt.tight_layout()  # 调整布局
    plt.show()  # 显示图形


# ====== 主程序入口 ======
if __name__ == "__main__":
    # ====== 全局变量存储结果 ======
    results = []  # 初始化结果列表

    # 加载数据
    data = load_digits()  # 加载手写数字数据集
    X, y = data.data, data.target  # 获取特征和标签
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=44)  # 划分训练集和测试集

    # 执行优化方法
    print("=== Grid Search ===")  # 打印网格搜索开始信息
    res_gs, time_gs = grid_search()  # 执行网格搜索
    record_result("Grid Search", res_gs['best_params'], res_gs['metrics'], time_gs)  # 记录网格搜索结果

    print("\n=== Random Search ===")  # 打印随机搜索开始信息
    res_rs, time_rs = random_search()  # 执行随机搜索
    record_result("Random Search", res_rs['best_params'], res_rs['metrics'], time_rs)  # 记录随机搜索结果

    print("\n=== Bayesian Optimization (Optuna) ===")  # 打印贝叶斯优化开始信息
    res_bo, time_bo = bayesian_optimization()  # 执行贝叶斯优化
    record_result("Bayesian Optimization", res_bo['best_params'], res_bo['metrics'], time_bo)  # 记录贝叶斯优化结果

    print("\n=== Hyperband Optimization ===")  # 打印Hyperband优化开始信息
    res_hb, time_hb = hyperband_optimization()  # 执行Hyperband优化
    record_result("Hyperband Optimization", res_hb['best_params'], res_hb['metrics'], time_hb)  # 记录Hyperband优化结果

    # 导出结果
    export_results()  # 导出结果到CSV文件
    display()  # 显示可视化结果

---

六、总结

6.1 核心结论

1. 贝叶斯优化综合性能最优：在准确率、效率和参数选择质量上全面领先，尤其适合高成本评估场景。
2. 随机搜索性价比高：在参数空间大时，能以较低成本找到接近最优的解，推荐作为初步探索工具。
3. 网格搜索适用性有限：仅在参数少、候选值明确时实用，否则计算成本过高。
4. Hyperband依赖场景特性：在手写数字识别这类早期性能与最终性能相关性弱的任务中表现不佳，但在深度学习等资源敏感型任务中可能更具优势。

6.2 实践建议

1. 组合使用多种方法：先用随机搜索快速缩小参数范围，再用贝叶斯优化精细化调优。
2. 监控优化过程：记录每个参数组合的性能和耗时，绘制收敛曲线，判断是否需要提前终止低效方法。
3. 领域知识结合：根据模型特性预设参数范围（如学习率通常在0.001-0.1之间），避免在无效区域搜索。
4. 考虑并行化：对计算密集型任务，利用分布式计算加速优化过程（如并行评估多个参数组合）。

通过合理选择和组合优化方法，能显著提升模型性能和开发效率，在实际项目中取得更好的效果。