文章目录
相关文章
Transformer架构:结构介绍:网页链接
Transformer架构:输入部分代码实现(基于PyTorch):网页链接
一、核心模块的整体作用
Transformer架构的强大性能源于四大核心模块的协同设计,它们通过分层协作实现了对序列数据的深度语义建模:
-
多头注意力机制(MultiHeadedAttention)
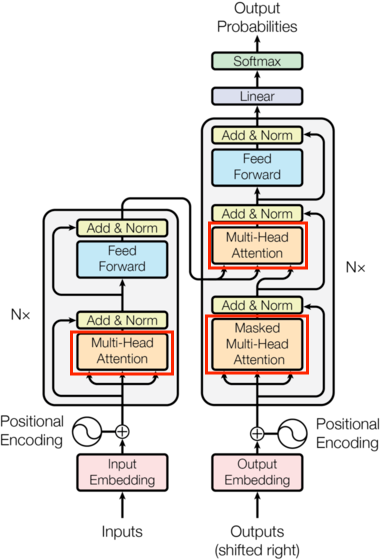
作为Transformer的“认知核心”,它通过将输入特征拆分到多个子空间(头),并行计算不同维度的注意力关联。这种设计让模型能同时捕捉多层面的语义关系——例如在文本处理中,一个头可能聚焦语法依赖(如主谓搭配),另一个头关注语义关联(如同义词替换),从而突破单头注意力的表达瓶颈。其核心是通过“查询-键-值”的交互模式,动态分配权重以突出关键信息。
-
前馈全连接层(PositionwiseFeedForward)
作为“特征增强器”,它对注意力输出进行非线性变换:通过“升维-激活-降维”的流程(如512→1024→512),将注意力捕捉的关联特征映射到更复杂的非线性空间。这种设计补充了注意力机制的线性局限,帮助模型学习高阶特征组合(如“上下文依赖+语义抽象”的复合模式),且对每个位置独立处理,兼顾效率与灵活性。

-
规范化层(LayerNorm)
作为“训练稳定器”,它通过对每个样本的特征维度进行均值-方差归一化,配合可学习的缩放与偏置参数,避免层间输出分布剧烈波动。与依赖批次统计的BatchNorm不同,LayerNorm在单样本上独立计算,不受批次大小影响,尤其适合序列长度可变的NLP任务,为深层网络的稳定训练提供保障。

-
子层连接结构(SublayerConnection)
作为“模块连接器”,它通过残差连接(输入与输出直接相加)与规范化、Dropout的结合,实现模块间的高效协同。残差连接解决了深层网络的梯度消失问题,让梯度能直接回传至浅层;规范化则确保每个子层的输入分布稳定;Dropout则通过随机失活抑制过拟合。这种“连接+正则”的设计,使多头注意力与前馈层能交替堆叠形成深层网络,最终实现对长距离依赖的精准建模。
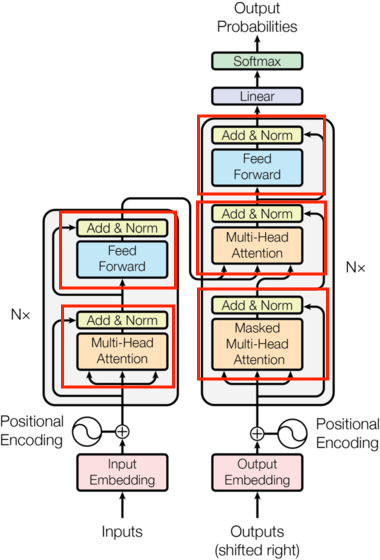
这四大模块形成“注意力捕捉关联→前馈增强特征→规范化稳定训练→残差连接深化网络”的闭环,共同支撑了Transformer在机器翻译、文本生成等任务中的卓越表现。
二、多头注意力机制(MultiHeadedAttention):并行捕捉多维度关联
在Transformer架构中,**多头注意力(Multi-Headed Attention)**是实现长距离依赖建模的核心组件。它通过将输入特征映射到多个子空间(头),并行计算注意力,从而同时捕捉不同语义维度的关联(如语法结构、语义相似性、位置关系等)。本文将结合流程图,详细解析多头注意力的实现逻辑,并对比代码实现与原论文的差异。
2.1 原理概述
注意力机制的核心是通过计算“查询(query)”与“键(key)”的相似度,为“值(value)”分配权重,公式为:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V Attention(Q,K,V)=softmax(dkQKT)V
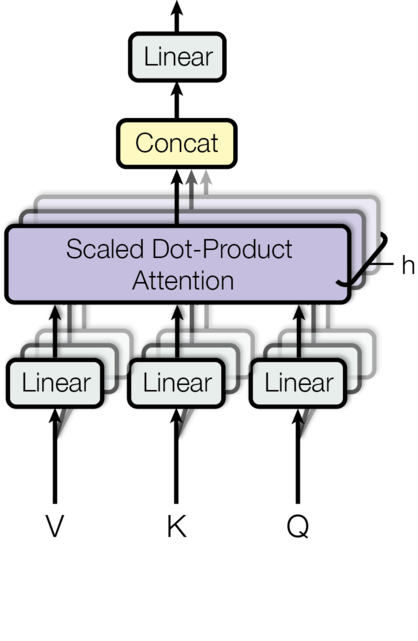
多头注意力在此基础上,将Q、K、V通过线性层拆分到 h h h个“头”(子空间),每个头独立计算注意力,最后拼接结果并通过线性层输出。公式为:
MultiHead
(
Q
,
K
,
V
)
=
Concat
(
head
1
,
.
.
.
,
head
h
)
W
O
\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O \\
MultiHead(Q,K,V)=Concat(head1,...,headh)WO
其中
head
i
=
Attention
(
Q
W
i
Q
,
K
W
i
K
,
V
W
i
V
)
\text{其中 } \text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)
其中 headi=Attention(QWiQ,KWiK,VWiV)
- 优势:每个头可捕捉不同语义子空间的关联(如语法、语义、位置等),提升模型表达能力。
- 关键创新:通过多头并行计算,突破单头注意力的表达瓶颈,同时利用参数共享降低计算复杂度。
2.2 代码实现与流程图解析
以下代码实现完整对应流程图中的三个核心阶段:初始化阶段、前向传播阶段和注意力计算阶段。
# 深度copy模型 输入模型对象和copy的个数 存储到模型列表中
def clones(module, N):
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
class MultiHeadedAttention(nn.Module):
def __init__(self, heads, embedding_dim, dropout=0.1):
super().__init__()
# 初始化阶段:验证输入合法性并配置基础参数
assert embedding_dim % heads == 0 # 确保词嵌入维度可被头数整除
self.d_k = embedding_dim // heads # 每个头的特征维度
self.heads = heads # 头的数量
self.linears = clones(nn.Linear(embedding_dim, embedding_dim), 4) # 4个线性层(Q/K/V + 输出)
self.attn = None # 存储注意力权重
self.dropout = nn.Dropout(p=dropout) # Dropout层
def forward(self, query, key, value, mask=None):
# 前向传播阶段:处理输入并执行多头注意力计算
if mask is not None:
mask = mask.unsqueeze(0) # 掩码升维以匹配多头结构
batch_size = query.size(0) # 获取批次大小
# 线性变换与多头拆分
query, key, value = [
model(x).view(batch_size, -1, self.heads, self.d_k).transpose(1, 2)
for model, x in zip(self.linears, (query, key, value))
]
# 注意力计算
x, self.attn = self.attention(query, key, value, mask=mask, dropout=self.dropout)
# 重组多头结果
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.heads * self.d_k)
# 最终线性变换
return self.linears[-1](x)
def attention(self, query, key, value, mask=None, dropout=None):
# 注意力计算阶段:核心逻辑实现
d_k = query.size(-1) # 每个头的特征维度
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k) # 计算注意力分数
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9) # 掩码处理
p_attn = F.softmax(scores, dim=-1) # 注意力权重归一化
if dropout is not None:
p_attn = dropout(p_attn) # Dropout正则化
attn_output = torch.matmul(p_attn, value) # 注意力加权输出
return attn_output, p_attn
完整结构图:
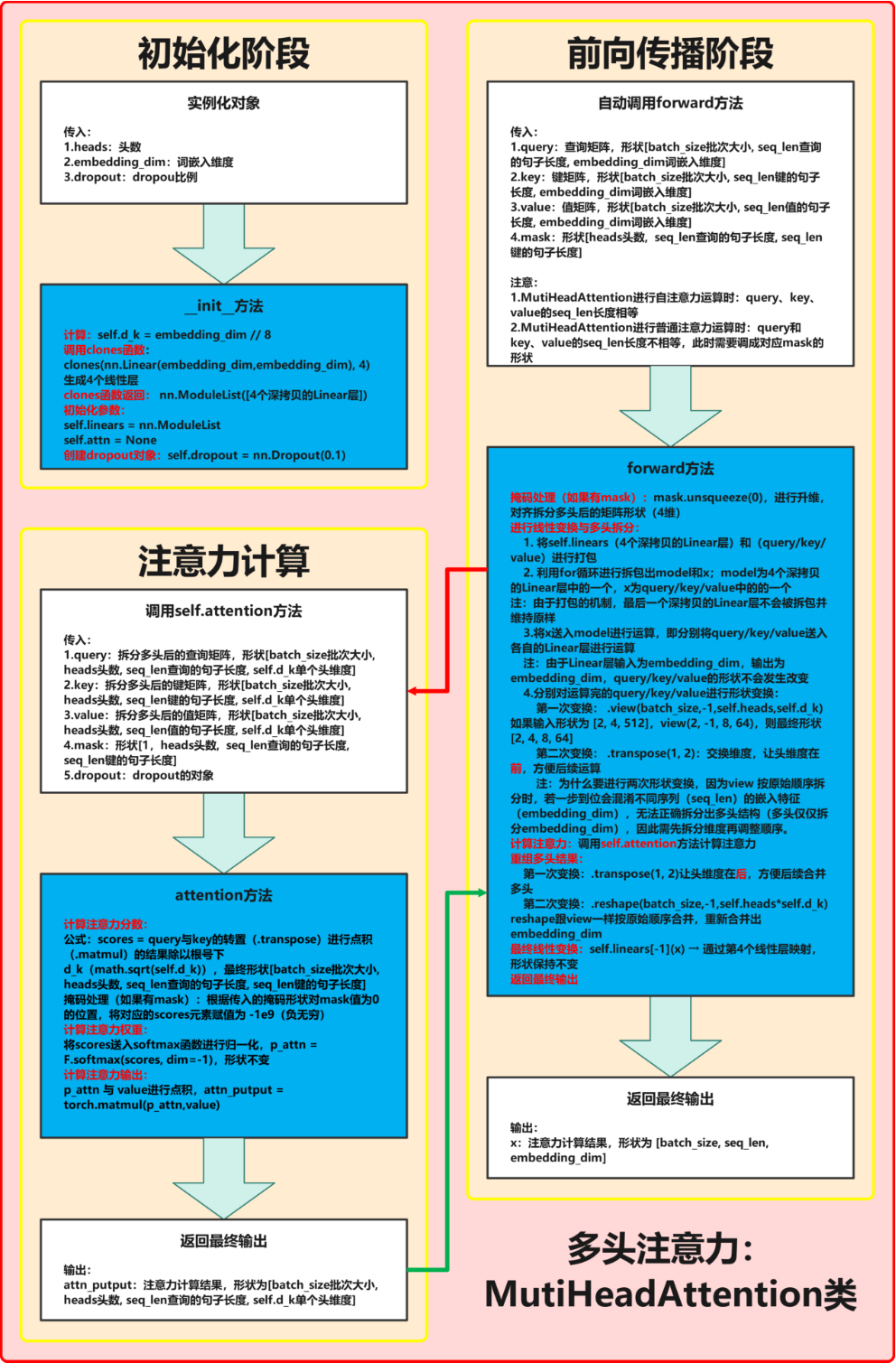
初始化阶段(__init__方法)

- 输入参数:
heads:头的数量(如8头)embedding_dim:词嵌入维度(如512)dropout:Dropout比例(如0.1)
- 核心计算:
self.d_k = embedding_dim // heads:计算每个头的特征维度(如512 // 8 = 64)self.linears = clones(...):生成4个线性层(用于Q/K/V变换和输出)
- 对象创建:
self.dropout = nn.Dropout(0.1):创建Dropout层
前向传播阶段(forward方法)

- 输入参数:
query:查询矩阵,形状[batch_size, seq_len_q, embedding_dim]key:键矩阵,形状[batch_size, seq_len_k, embedding_dim]value:值矩阵,形状[batch_size, seq_len_v, embedding_dim]mask:掩码矩阵,形状[heads, seq_len_q, seq_len_k]
- 关键步骤:
- 掩码升维:
mask.unsqueeze(0)调整掩码形状以匹配多头结构 - 线性变换与多头拆分:
query, key, value = [ model(x).view(batch_size, -1, self.heads, self.d_k).transpose(1, 2) for model, x in zip(self.linears, (query, key, value)) ]- 输入形状变化:
[batch_size, seq_len, 512]→[batch_size, seq_len, 8, 64]→[batch_size, 8, seq_len, 64]
- 输入形状变化:
- 注意力计算:调用
self.attention(...) - 重组多头结果:
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.heads * self.d_k)- 输出形状变化:
[batch_size, 8, seq_len, 64]→[batch_size, seq_len, 512]
- 输出形状变化:
- 最终线性变换:
self.linears[-1](x)输出结果
- 掩码升维:
注意力计算阶段(attention方法)

- 输入参数:
query:拆分后的查询矩阵,形状[batch_size, heads, seq_len_q, d_k]key:拆分后的键矩阵,形状[batch_size, heads, seq_len_k, d_k]value:拆分后的值矩阵,形状[batch_size, heads, seq_len_v, d_k]mask:掩码矩阵,形状[1, heads, seq_len_q, seq_len_k]dropout:Dropout对象
- 核心计算:
- 注意力分数:
torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k) - 掩码处理:
scores.masked_fill(mask == 0, -1e9) - 权重归一化:
F.softmax(scores, dim=-1) - Dropout:
dropout(p_attn)(可选) - 加权输出:
torch.matmul(p_attn, value)
- 注意力分数:
2.3 代码实现与原论文的区别
在代码实现中,多头注意力的计算顺序是先进行线性变换,再拆分多头;而原论文中是先拆分多头,再对每个头进行线性变换。具体差异如下:
-
代码实现逻辑:
- 输入Q、K、V首先通过各自的线性层(
self.linears)进行变换。 - 变换后的Q、K、V被拆分为多个头(
view和transpose操作)。 - 每个头独立计算注意力分数和权重。
- 最后将所有头的结果拼接并通过输出线性层。
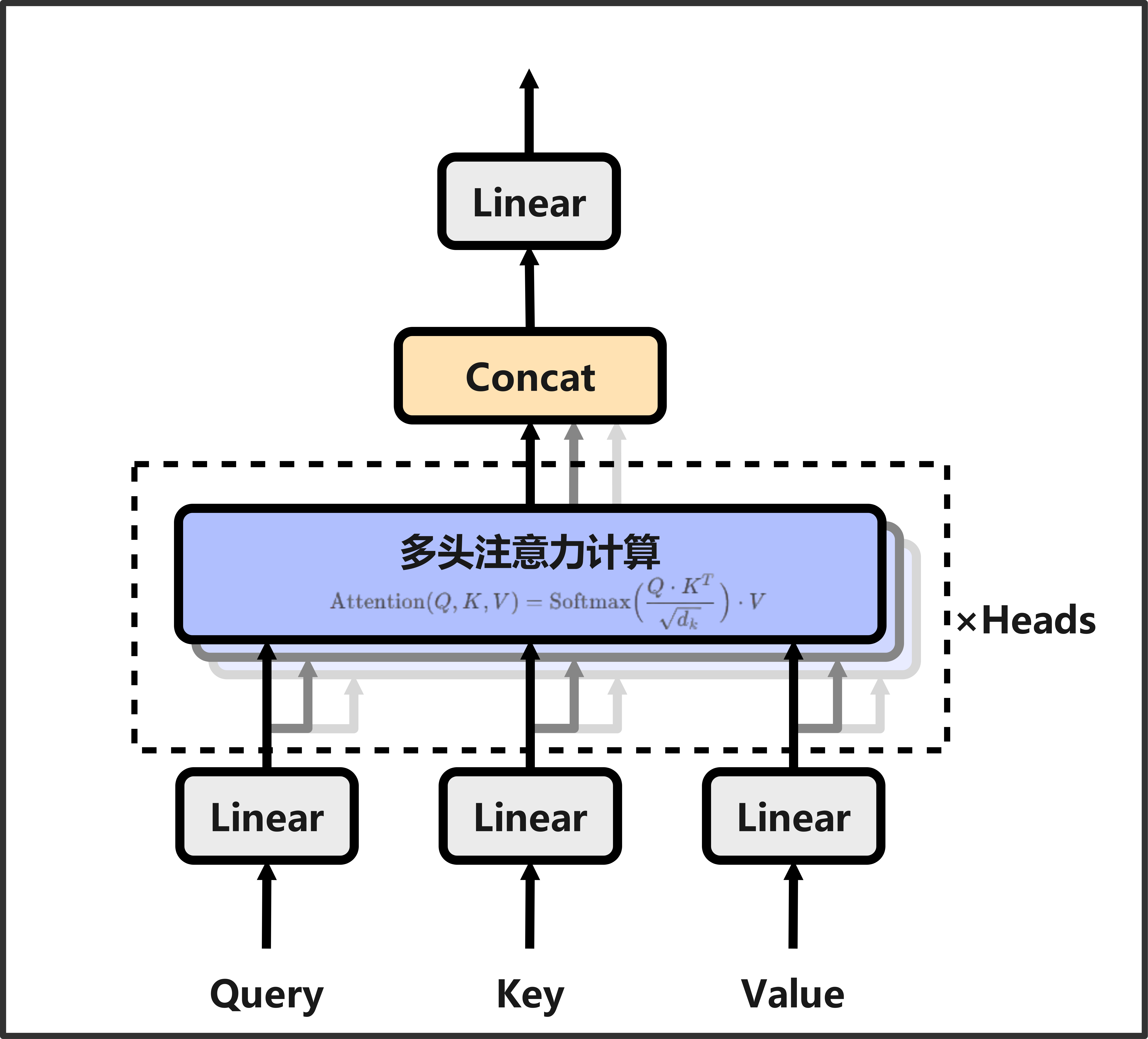
- 输入Q、K、V首先通过各自的线性层(
-
原论文逻辑:
- 输入Q、K、V首先被拆分为多个头。
- 每个头的Q、K、V分别通过各自的线性层进行变换。
- 每个头独立计算注意力分数和权重。
- 最后将所有头的结果拼接并通过输出线性层。
差异总结:
- 代码实现:线性变换在前,多头拆分在后。优点是实现简洁,利用广播机制减少代码复杂度。
- 原论文:多头拆分在前,线性变换在后。优点是每个头的线性变换参数独立,理论上更灵活,但实现复杂度较高。
2.4 关键细节解析
- 多头拆分:通过
view和transpose将embedding_dim=512拆分为8个头(每个头64维),使模型能并行学习不同子空间的关联。例如,一个头可能关注语法依赖,另一个关注语义相似性。 - 缩放点积:分数除以 d k \sqrt{d_k} dk(如 64 = 8 \sqrt{64}=8 64=8)是为了避免维度过高时内积值过大,导致softmax梯度消失(值过大时softmax输出接近one-hot,梯度趋近于0)。
- 掩码作用:
masked_fill(mask == 0, -1e9)确保模型在计算注意力时忽略无效位置(如填充的PAD token),避免其影响权重分配。
三、前馈全连接层(PositionwiseFeedForward):增强非线性表达
3.1 原理概述
前馈全连接层对注意力输出进行非线性变换,公式为:
FFN ( x ) = W 2 ⋅ ReLU ( W 1 x + b 1 ) + b 2 \text{FFN}(x) = W_2 \cdot \text{ReLU}(W_1 x + b_1) + b_2 FFN(x)=W2⋅ReLU(W1x+b1)+b2
- 作用:对每个位置的特征独立进行线性变换+非线性激活,增强模型对复杂模式的捕捉能力。
- 设计:中间层维度通常是嵌入维度的2-4倍(如配置中d_ff=1024,是512的2倍),通过升维再降维实现更丰富的特征组合。
3.2 代码实现与流程图解析
根据流程图,前馈全连接层的实现分为两个主要阶段:初始化阶段和前向传播阶段。
class PositionwiseFeedForward(nn.Module):
def __init__(self, embedding_dim, d_ff, dropout=0.1):
"""
初始化前馈全连接层
参数:
embedding_dim: 词嵌入维度(输入和输出的特征维度)
d_ff: 中间隐藏层的特征维度
dropout: Dropout概率
"""
super().__init__()
# 初始化阶段:创建网络层和Dropout对象
self.w1 = nn.Linear(embedding_dim, d_ff) # 第一层神经网络
self.w2 = nn.Linear(d_ff, embedding_dim) # 第二层神经网络
self.dropout = nn.Dropout(p=dropout) # Dropout对象
def forward(self, x):
"""
前向传播过程
参数:
x: 输入张量,形状为 [batch_size, seq_len, embedding_dim]
返回:
处理后的张量,形状为 [batch_size, seq_len, embedding_dim]
"""
# 前向传播阶段:数据经过网络层和激活函数
x = self.w1(x) # 经过第一层神经网络
x = F.relu(x) # 经过激活函数
x = self.dropout(x) # 经过Dropout处理
x = self.w2(x) # 经过第二层神经网络
return x
完整结构图:
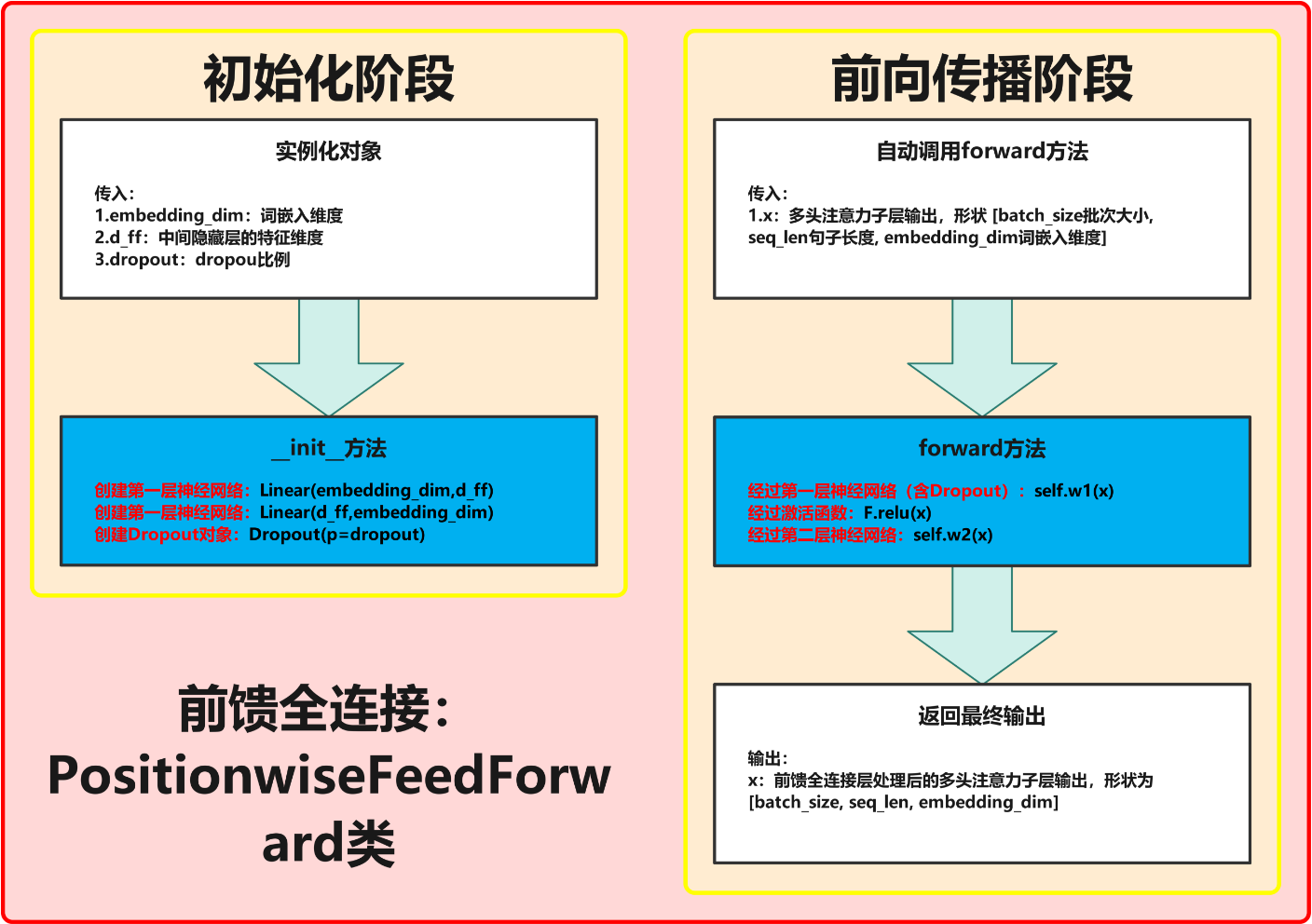
初始化阶段(__init__方法)
- 输入参数:
embedding_dim:词嵌入维度(输入和输出的特征维度)d_ff:中间隐藏层的特征维度dropout:Dropout概率
- 核心操作:
- 创建第一层神经网络:
nn.Linear(embedding_dim, d_ff) - 创建第二层神经网络:
nn.Linear(d_ff, embedding_dim) - 创建Dropout对象:
nn.Dropout(p=dropout)
- 创建第一层神经网络:
前向传播阶段(forward方法)
- 输入参数:
x:多头注意力子层输出,形状为[batch_size, seq_len, embedding_dim]
- 关键步骤:
- 第一层神经网络:
self.w1(x),将输入特征从embedding_dim映射到d_ff - 激活函数:
F.relu(x),引入非线性特性 - Dropout处理:
self.dropout(x),正则化防止过拟合 - 第二层神经网络:
self.w2(x),将特征从d_ff映射回embedding_dim
- 第一层神经网络:
- 输出:
- 处理后的张量,形状为
[batch_size, seq_len, embedding_dim]
- 处理后的张量,形状为
3.3 关键细节解析
- 位置无关性:与RNN不同,前馈层对每个位置独立处理(无序列依赖),因此称为"Positionwise"。这种设计配合注意力机制的全局依赖,兼顾效率与表达能力。
- 非线性作用:ReLU激活函数引入非线性,使模型能学习更复杂的特征映射(如语义组合、上下文关联)。
- 维度变换:通过"升维-非线性变换-降维"的结构,增强模型的特征表达能力。
四、规范化层(LayerNorm):稳定训练过程
4.1 原理概述
规范化层的作用是将输入特征归一化到稳定分布(均值0、方差1),公式为:
LayerNorm ( x ) = γ ⋅ x − μ σ 2 + ϵ + β \text{LayerNorm}(x) = \gamma \cdot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta LayerNorm(x)=γ⋅σ2+ϵx−μ+β
其中 μ \mu μ和 σ 2 \sigma^2 σ2是输入 x x x在特征维度上的均值和方差, γ \gamma γ(a2)和 β \beta β(b2)是可学习的缩放和平移参数, ϵ \epsilon ϵ是防止分母为0的小值。
- 与BatchNorm的区别:LayerNorm在单个样本的特征维度上计算均值和方差(如对[2,4,512]中的512维计算),而BatchNorm在批次维度上计算,更适合序列数据(样本长度可变)。
4.2 代码实现与流程图解析
根据流程图,层规范化的实现分为两个主要阶段:初始化阶段和前向传播阶段。
class LayerNorm(nn.Module):
def __init__(self, embedding_dim, eps=1e-6):
super().__init__()
# 初始化阶段:定义可学习参数
self.a2 = nn.Parameter(torch.ones(embedding_dim)) # 规范化层权重
self.b2 = nn.Parameter(torch.zeros(embedding_dim)) # 规范化层偏置
self.eps = eps # 防止除零的小常数
def forward(self, x):
# 前向传播阶段:计算均值、标准差并应用层规范化
mean = x.mean(dim=-1, keepdim=True) # 计算均值
std = x.std(dim=-1, keepdim=True) # 计算标准差
# 应用层规范化
return self.a2 * (x-mean) / (std + self.eps) + self.b2
完整结构图:

初始化阶段(__init__方法)
- 输入参数:
embedding_dim:词嵌入维度eps:防止除零的小常数,默认1e-6
- 核心操作:
- 定义规范化层权重:
nn.Parameter(torch.ones(embedding_dim)) - 定义规范化层偏置:
nn.Parameter(torch.zeros(embedding_dim)) - 这些参数通过反向传播自动更新
- 定义规范化层权重:
前向传播阶段(forward方法)
- 输入参数:
x:输入张量,形状为[batch_size, seq_len, embedding_dim]
- 关键步骤:
- 计算均值:
x.mean(dim=-1, keepdim=True),形状为[batch_size, seq_len, 1] - 计算标准差:
x.std(dim=-1, keepdim=True),形状为[batch_size, seq_len, 1] - 应用层规范化:
self.a2 * (x-mean) / (std + self.eps) + self.b2
- 计算均值:
- 输出:
- 规范化后的张量,形状为
[batch_size, seq_len, embedding_dim]
- 规范化后的张量,形状为
4.3 关键细节解析
- 可学习参数:a2和b2允许模型调整归一化后的分布(不一定是标准正态),保留有用特征的量级信息(如重要的语义特征可能需要更大的值)。
- 稳定梯度:归一化后的输入使权重更新更稳定,避免梯度消失(值过小)或爆炸(值过大),尤其在深层Transformer中至关重要。
- 维度保持:通过
keepdim=True保持维度不变,确保张量形状匹配,便于后续计算。
五、子层连接结构(SublayerConnection):残差连接+规范化
5.1 原理概述
子层连接将"子层"(注意力层或前馈层)的输出与输入通过残差连接结合,并应用规范化,公式为:
SublayerConnection ( x ) = x + Dropout ( LayerNorm ( Sublayer ( x ) ) ) \text{SublayerConnection}(x) = x + \text{Dropout}(\text{LayerNorm}(\text{Sublayer}(x))) SublayerConnection(x)=x+Dropout(LayerNorm(Sublayer(x)))
(注:两种顺序均常见,核心是残差+规范化)
- 作用:残差连接( x + . . . x + ... x+...)帮助梯度直接传播(避免深层网络梯度衰减),规范化稳定中间结果分布。
5.2 代码实现与流程图解析
根据流程图,子层连接结构的实现分为两个主要阶段:初始化阶段和前向传播阶段。
class SublayerConnection(nn.Module):
def __init__(self, embedding_dim, dropout=0.1):
super().__init__()
# 初始化阶段:创建规范化层和Dropout层
self.norm = LayerNorm(embedding_dim) # 规范化层
self.dropout = nn.Dropout(dropout) # Dropout层
def forward(self, x, sublayer):
# 前向传播阶段:子层处理、规范化和残差连接
myres = x +self.dropout(self.norm(sublayer(x)))
return myres
完整结构图:

初始化阶段(__init__方法)
- 输入参数:
embedding_dim:词嵌入维度dropout:Dropout概率
- 核心操作:
- 创建规范化层:
LayerNorm(embedding_dim) - 创建Dropout层:
nn.Dropout(dropout)
- 创建规范化层:
前向传播阶段(forward方法)
- 输入参数:
x:上一子层输出,形状为[batch_size, seq_len, embedding_dim]sublayer:子层对象(多头注意力层或前馈全连接层)
- 关键步骤:
- 子层处理:
sublayer(x),获取子层模块输出 - 规范化处理:
self.norm(sublayer_output),将子层输出送入规范化层 - 残差连接:
x + self.dropout(normed_output),进行残差连接
- 子层处理:
- 输出:
- 处理后的张量,形状为
[batch_size, seq_len, embedding_dim]
- 处理后的张量,形状为
5.3 关键细节解析
- 子层灵活性:通过传入不同的
sublayer对象(如多头注意力层或前馈全连接层),实现通用的连接结构,简化编码器/解码器的实现。 - Dropout作用:在子层输出后应用dropout,随机丢弃部分特征,防止模型过度依赖特定子层的输出,增强泛化能力。
- 残差连接:通过将原始输入与子层输出相加,有效缓解了深层网络中的梯度消失问题,使模型能够训练更深的网络。
六、完整代码
from Transformer_input import *
# 多头注意力机制类 MultiHeadedAttention 实现思路分析
# 1 init函数 (self, head, embedding_dim, dropout=0.1)
# 每个头特征尺寸大小self.d_k 多少个头self.head 线性层列表self.linears
# self.linears = clones(nn.Linear(embedding_dim, embedding_dim), 4)
# 注意力权重分布self.attn=None dropout层self.dropout
# 2 forward(self, query, key, value, mask=None)
# 2-1 掩码增加一个维度[8,4,4] -->[1,8,4,4] 求多少批次batch_size
# 2-2 数据经过线性层 切成8个头,view(batch_size, -1, self.head, self.d_k), transpose(1,2)数据形状变化
# 数据形状变化[2,4,512] ---> [2,4,8,64] ---> [2,8,4,64]
# 2-3 24个头 一起送入到attention函数中求 x, self.attn
# attention([2,8,4,64],[2,8,4,64],[2,8,4,64],[1,8,4,4]) ==> x[2,8,4,64], self.attn[2,8,4,4]]
# 2-4 数据形状再变化回来 x.transpose(1,2).contiguous().view(,,)
# 数据形状变化 [2,8,4,64] ---> [2,4,8,64] ---> [2,4,512]
# 2-5 返回最后线性层结果 return self.linears[-1](x)
# 深度copy模型 输入模型对象和copy的个数 存储到模型列表中
def clones(module,N):
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
class MutiHeadAttention(nn.Module):
def __init__(self,heads,embedding_dim,dropout=0.1):
super().__init__()
# 确认数据特征能否被被整除 eg 特征尺寸512 % 头数8
assert embedding_dim % heads == 0
# 计算每个头特征尺寸 特征尺寸512 // 头数8 = 64
self.d_k = embedding_dim //heads
# 多少头数
self.heads = heads
# 四个线性层
self.linears = clones(nn.Linear(embedding_dim,embedding_dim),4)
# 注意力权重分布
self.attn = None
# dropout层
self.dropout = nn.Dropout(p=dropout)
def forward(self,query,key,value,mask=None):
# 若使用掩码,则掩码增加一个维度[8,4,4] -->[1,8,4,4]
if mask is not None:
mask = mask.unsqueeze(0)
# 数据形状变化[2,4,512] ---> [2,4,8,64] ---> [2,8,4,64]
# 4代表4个单词 8代表8个头 让句子长度4和句子特征64靠在一起 更有利捕捉句子特征
query,key,value = [model(x).view(batch_size,-1,self.heads,self.d_k).transpose(1,2) for model,x in zip(self.linears,(query,key,value))]
# myoutptlist_data = []
# for model, x in zip(self.linears, (query, key, value)):
# print('x--->', x.shape) # [2,4,512]
# myoutput = model(x)
# print('myoutput--->', myoutput.shape) # [2,4,512]
# # [2,4,512] --> [2,4,8,64] --> [2,8,4,64]
# tmpmyoutput = myoutput.view(batch_size, -1, self.head, self.d_k).transpose(1, 2)
# myoutptlist_data.append( tmpmyoutput )
# mylen = len(myoutptlist_data) # mylen:3
# query = myoutptlist_data[0] # [2,8,4,64]
# key = myoutptlist_data[1] # [2,8,4,64]
# value = myoutptlist_data[2] # [2,8,4,64]
# 注意力结果表示x形状 [2,8,4,64] 注意力权重attn形状:[2,8,4,4]
# attention([2,8,4,64],[2,8,4,64],[2,8,4,64],[1,8,4,4]) ==> x[2,8,4,64], self.attn[2,8,4,4]]
x,self.attn = self.attention(query,key,value,mask=mask,dropout=self.dropout)
# 数据形状变化 [2,8,4,64] ---> [2,4,8,64] ---> [2,4,512]
x = x.transpose(1,2).reshape(batch_size,-1,self.heads*self.d_k)
# 返回最后变化后的结果 [2,4,512]---> [2,4,512]
x = self.linears[-1](x)
return x
# 自注意力机制函数attention 实现思路分析
# attention(query, key, value, mask=None, dropout=None)
# 1 求查询张量特征尺寸大小 d_k
# 2 求查询张量q的权重分布socres q@k^T /math.sqrt(d_k)
# 形状[2,4,512] @ [2,512,4] --->[2,4,4]
# 3 是否对权重分布scores进行 scores.masked_fill(mask == 0, -1e9)
# 4 求查询张量q的权重分布 p_attn F.softmax()
# 5 是否对p_attn进行dropout if dropout is not None:
# 6 求查询张量q的注意力结果表示 [2,4,4]@[2,4,512] --->[2,4,512]
# 7 返回q的注意力结果表示 q的权重分布
def attention(self,query,key,value,mask=None,dropout=None):
# query, key, value:代表注意力的三个输入张量
# mask:代表掩码张量
# dropout:传入的dropout实例化对象
# 2 求查询张量q的权重分布socres q@k^T /math.sqrt(d_k)
# [2,4,512] @ [2,512,4] --->[2,4,4]
scores = torch.matmul(query,key.transpose(-2,-1)/math.sqrt(self.d_k))
# 3 是否对权重分布scores 进行 masked_fill
if mask is not None:
# 根据mask矩阵0的位置 对sorces矩阵对应位置进行掩码
scores = scores.masked_fill(mask == 0 , -1e9)
# 4 求查询张量q的权重分布 softmax
p_attn = F.softmax(scores,dim=-1)
# 5 是否对p_attn进行dropout
if dropout is not None:
p_attn = dropout(p_attn)
# 查询张量q的注意力结果表示 bmm-matmul运算, 注意力查询张量q的权重分布p_attn
# [2,4,4]*[2,4,512] --->[2,4,512]
attn_putput = torch.matmul(p_attn,value)
return attn_putput,p_attn
# 前馈全连接层 PositionwiseFeedForward 实现思路分析
# 1 init函数 (self, d_model, d_ff, dropout=0.1):
# 定义线性层self.w1 self.w2, self.dropout层
# 2 forward(self, x)
# 数据经过self.w1(x) -> F.relu() ->self.dropout() ->self.w2 返回
class PositionwiseFeedForward(nn.Module):
def __init__(self,embedding_dim,d_ff,dropout=0.1):
# d_model 第1个线性层输入维度
# d_ff 第2个线性层输出维度
super().__init__()
# 定义线性层w1 w2 dropout
self.w1 = nn.Linear(embedding_dim,d_ff)
self.w2 = nn.Linear(d_ff,embedding_dim)
self.dropout = nn.Dropout(p=dropout)
def forward(self,x):
x = self.w1(x)
x = F.relu(x)
x = self.dropout(x)
x = self.w2(x)
return x
# 规范化层 LayerNorm 实现思路分析
# 1 init函数 (self, features, eps=1e-6):
# 定义线性层self.a2 self.b2, nn.Parameter(torch.ones(features))
# 2 forward(self, x) 返回标准化后的结果
# 对数据求均值 保持形状不变 x.mean(-1, keepdims=True)
# 对数据求方差 保持形状不变 x.std(-1, keepdims=True)
# 对数据进行标准化变换 反向传播可学习参数a2 b2
# eg self.a2 * (x-mean)/(std + self.eps) + self.b2
class LayerNorm(nn.Module):
def __init__(self,embedding_dim,eps = 1e-6):
# 参数features 待规范化的数据
# 参数 eps=1e-6 防止分母为零
super().__init__()
# 定义a2 规范化层的系数 y=kx+b中的k
self.a2 = nn.Parameter(torch.ones(embedding_dim))
# 定义b2 规范化层的系数 y=kx+b中的b
self.b2 = nn.Parameter(torch.zeros(embedding_dim))
self.eps = eps
def forward(self,x):
# 对数据求均值 保持形状不变
# [2,4,512] -> [2,4,1]
mean = x.mean(-1,keepdims=True)
# 对数据求方差 保持形状不变
# [2,4,512] -> [2,4,1]
std = x.std(-1,keepdim=True)
# 对数据进行标准化变换 反向传播可学习参数a2 b2
# 注意 * 表示对应位置相乘 不是矩阵运算
y = self.a2 * (x-mean)/(std+self.eps)+self.b2
return y
# 子层连接结构 子层(前馈全连接层 或者 注意力机制层)+ norm层 + 残差连接
# SublayerConnection实现思路分析
# 1 init函数 (self, size, dropout=0.1):
# 定义self.norm层 self.dropout层, 其中LayerNorm(size)
# 2 forward(self, x, sublayer) 返回+以后的结果
# 数据self.norm() -> sublayer()->self.dropout() + x
class SublayerConnection(nn.Module):
def __init__(self,embedding_dim,dropout=0.1):
# 参数size 词嵌入维度尺寸大小
# 参数dropout 置零比率
super().__init__()
# 定义norm层
self.norm = LayerNorm(embedding_dim)
# 定义dropout
self.dropout = nn.Dropout(dropout)
def forward(self,x,sublayer):
# 参数x 代表数据
# sublayer 函数入口地址 子层函数(前馈全连接层 或者 注意力机制层函数的入口地址)
# 方式1 # 数据self.norm() -> sublayer()->self.dropout() + x
# myres = x + self.dropout(sublayer(self.norm(x)))
# 方式2 # 数据sublayer() -> self.norm() ->self.dropout() + x
myres = x +self.dropout(self.norm(sublayer(x)))
return myres

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








