文章目录
本文是笔者进行神经网络学习的个人学习日记
图片和链接均源自网络,侵删
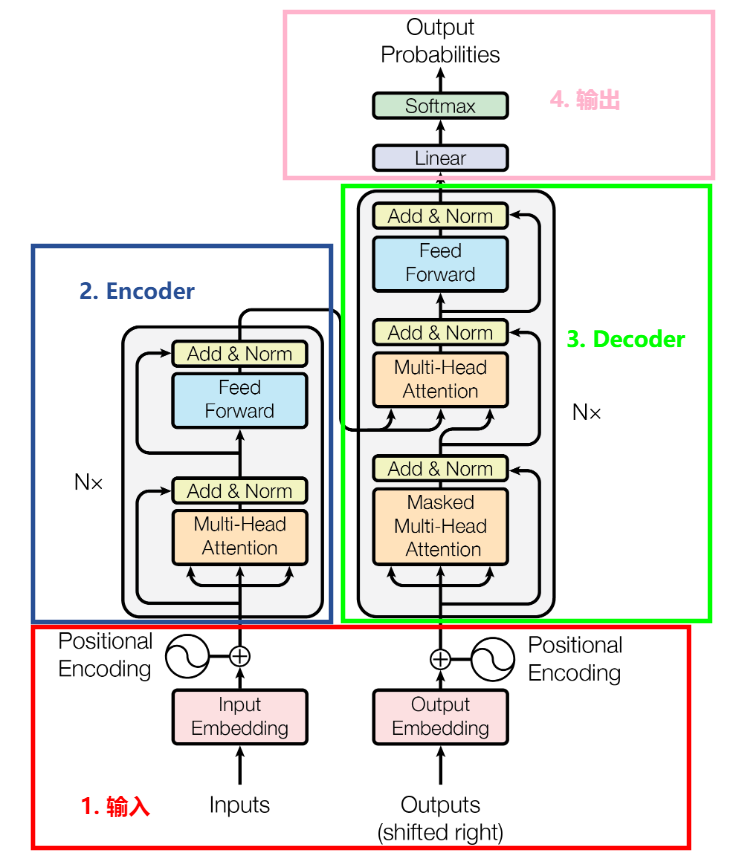
1 Transformer框架图
Transformer是一个基于Encoder-Decoder框架的模型,模型结构如下图,主要分为4个模块:输入输出和Encoder-Decoder。其中,Nx为Encoder和Decoder堆叠的个数。
史上最小白之Attention详解:https://blog.youkuaiyun.com/Tink1995/article/details/105012972
史上最小白之Transformer详解:https://blog.youkuaiyun.com/Tink1995/article/details/105080033
2 Encoder-Decoder结构
一个简单的Encoder-Decoder框架图如下所示。
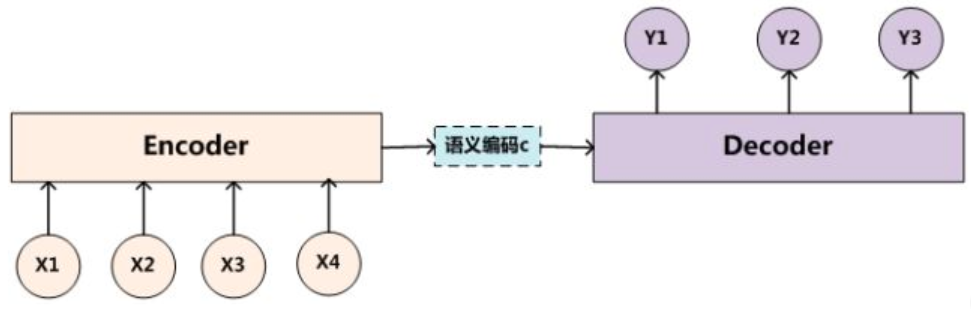
对于序列 < x 1 , x 2 , … , x n > <x_1,x_2,\dots,x_n> <x1,x2,…,xn>,Encoder会将其转化成一个语义编码C,这个C中储存了序列 < x 1 , x 2 , … , x n > <x_1,x_2,\dots,x_n> <x1,x2,…,xn>的信息。编码的方式有很多种,例如RNN/LSTM/GRU等。接下来,Decoder就要对语义编码C进行解码,方式也可以采用上述各种模型。
3 注意力机制
首先引入几个概念:
- 查询(Query):查询的范围,即主观意识的特征向量
- 键(Key):被比对的项,即物体的突出特征信息向量
- 值(Value):物体本身的特征向量,通常与Key成对出现
注意力机制就是通过Query和Key的注意力汇聚(给定一个Q,计算Q和K的相关性,然后根据相关性找合适的V)实现对Value的注意力权重分配,生成最终的输出结果。
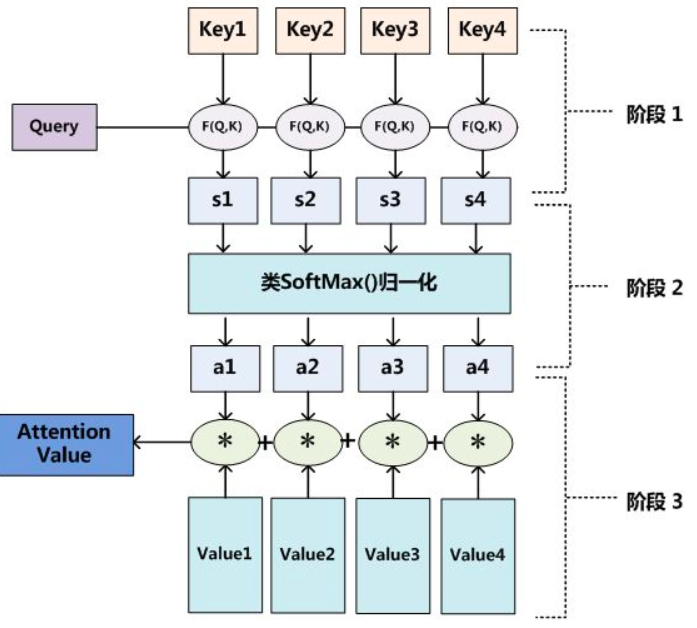
3.1 注意力机制计算过程
共分为三个阶段:
-
阶段一:根据计算Q和K之间的相关性(相似性),得到注意力得分,常见的相似性计算如点积(Transformer用的方法)、余弦相似度、MLP等:
- 点积: S i m ( Q , K i ) = Q ⋅ K i Sim(Q,K_i)=Q\cdot K_i Sim(Q,Ki)=Q⋅Ki
- 余弦相似度: S i m ( Q , K i ) = Q ⋅ K i ∣ ∣ Q ∣ ∣ ⋅ ∣ ∣ K i ∣ ∣ Sim(Q,K_i)=\frac{Q\cdot K_i}{||Q||\cdot||K_i||} Sim(Q,Ki)=∣∣Q∣∣⋅∣∣Ki∣∣Q⋅Ki
- MLP网络: S i m ( Q , K i ) = M L P ( Q , K i ) Sim(Q,K_i)=MLP(Q,K_i) Sim(Q,Ki)=MLP(Q,Ki)
-
阶段二:对注意力得分进行scale(一般 ÷ d K \div\sqrt{d_K} ÷dK即根号K的纬度)后,利用一个Softmax函数计算权重 a i a_i ai:
a i = S o f t m a x ( S i m i ) = e S i m i ∑ j = 1 L x e S i m j a_i=Softmax(Sim_i)=\frac{e^{Sim_i}}{\sum^{L_x}_{j=1}e^{Sim_j}} ai=Softmax(Simi)=∑j=1LxeSimjeSimi
其中, L x L_x Lx是Source的长度。 -
阶段三:上一步的计算结果 a i a_i ai即 V i Vi Vi对应的权重系数,进行加权求和得到Attention数值:
A t t e n t i o n ( Q , S o u r c e ) = ∑ i = 1 L x a i ⋅ V a l u e i Attention(Q,Source)=\sum^{L_x}_{i=1}a_i\cdot Value_i Attention(Q,Source)=i=1∑Lxai⋅Valuei
整体流程如下两张图:
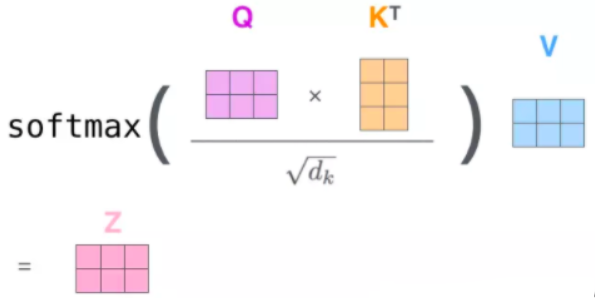
3.2 Self-Attention
由于神经网络接收的输入是很多大小不一的向量,并且不同向量之间有一定的关系,但实际训练时无法充分发挥其之间的关系导致模型训练结果效果差。因此,针对全连接神经网络对于多个相关的输入无法建立起相关性的问题,就可以用自注意力机制来解决,即让机器注意到不同部分之间的相关性。
自注意力机制与注意力机制相比,减少了对外部信息的依赖,它的Q、K、V来自同一组元素X,需要找到的也是X中的关键点。例如,在英-中机器翻译中,Source是英文句子,Target是翻译出的中文句子,Attention机制发生在Target的元素和Source中的所有元素之间。而Self Attention顾名思义,指的不是Target和Source之间的Attention机制,而是Source内部元素之间或者Target内部元素之间发生的Attention机制,也可以理解为Target=Source这种特殊情况下的注意力计算机制。
至于计算方法,与普通的注意力机制是相同的,只不过输入从Q、K、V变成了源X中的多个向量 X i X_i Xi。
- 阶段一:对于每个向量 X i X_i Xi,分别乘上三个权重矩阵 W Q W^Q WQ、 W K W^K WK、 W V W^V WV,得到Q、K、V,然后计算Q和K相似性(注意力得分)。
- 阶段二:对得分进行scale后,使用Softmax归一,得到权重矩阵。
- 阶段三:使用刚才得到的权重矩阵,与V相乘,计算加权求和。
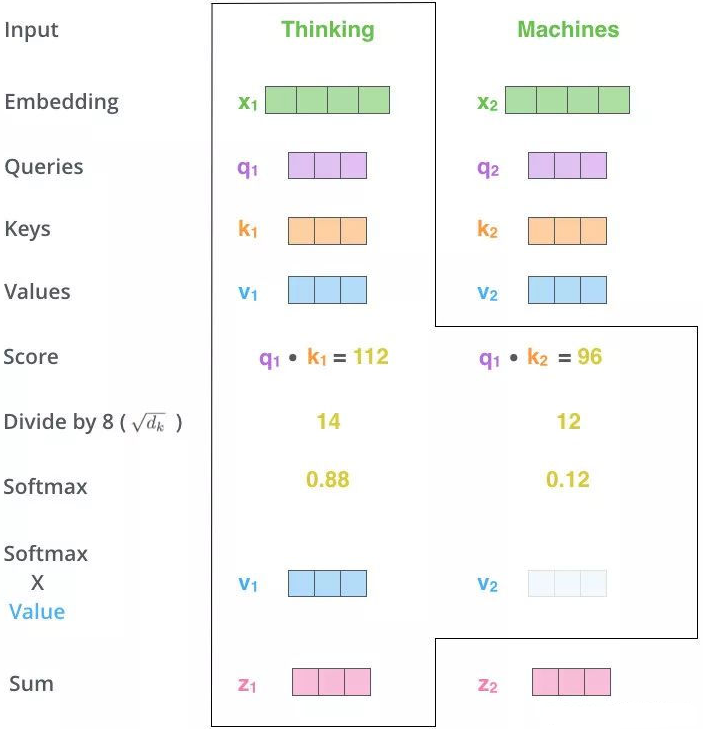
上图展示对Thinking Machines这句话进行自注意力的全过程,最终得到z1和z2两个新向量。
其中z1表示的是thinking这个词向量的新的向量表示(通过thinking这个词向量,去查询和thinking machine这句话里面每个单词和thinking之间的相似度)。也就是说新的z1依然是thinking的词向量表示,只不过这个词向量的表示蕴含了thinking machines这句话对于thinking而言哪个更重要的信息。
3.3 Multi-Head Attention
自注意力机制对当前位置信息进行编码时,可能会过度将注意力集中于自身的位置,有效信息的抓取能力就差一些。因此,提出了多头注意力机制,当给定相同的查询、键和值的集合时, 我们希望模型可以基于相同的注意力机制学习到不同的行为, 然后将不同的行为作为知识组合起来, 捕获序列内各种范围的依赖关系。
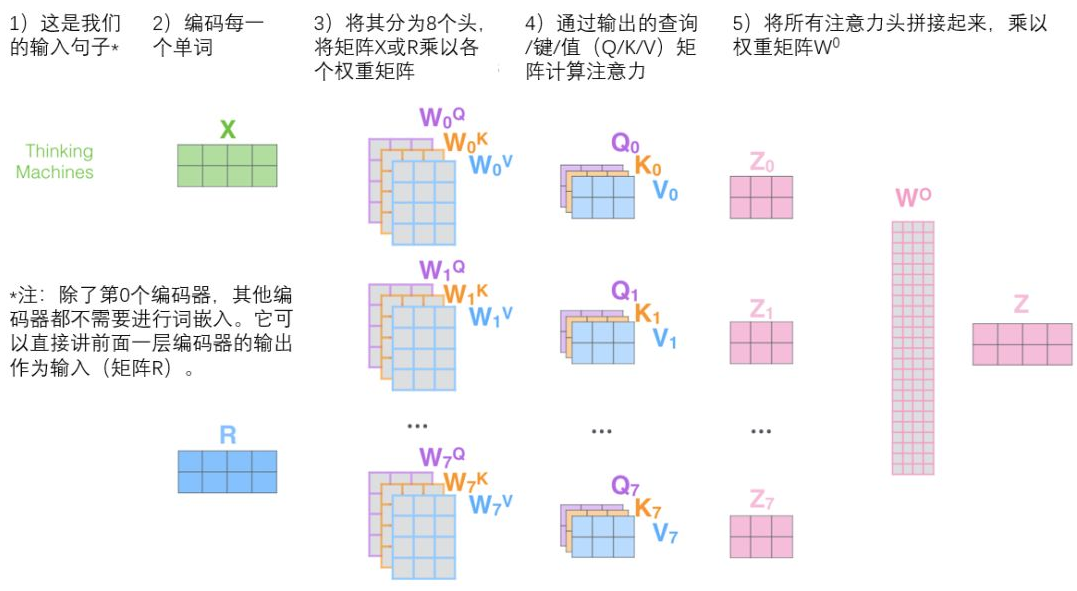
对于输入的embedding矩阵,self-attention只使用了一组 W Q W^Q WQ、 W K W^K WK、 W V W^V WV来进行变换得到Query,Keys,Values。而Multi-Head Attention使用多组得 W Q W^Q WQ、 W K W^K WK、 W V W^V WV到多组Query,Keys,Values,然后每组分别计算得到一个Z矩阵,最后将得到的多个Z矩阵进行拼接。Transformer里面是使用了8组不同的 W Q W^Q WQ、 W K W^K WK、 W V W^V WV。那么整体流程就成了下图这样:
3.4 Masked Multi-Head Attention
Mask表示掩码,它对某些值进行掩盖,使其在参数更新时不产生效果。Transformer模型中涉及两种 mask,分别是:
- padding mask:因为每个批次输入序列长度不同,我们要对输入序列进行对齐,在较短的序列后面填充 0。但是如果输入的序列太长,则是截取左边的内容,把多余的直接舍弃,即加上一个负无穷,使其经过Softmax后,这些位置的概率就会接近0。
- sequence mask:对于一个序列,如果要预测time_step为t的时刻,我们的解码输出应该只能依赖于t时刻之前的输出,而不能依赖t之后的输出。而训练时则是需要完整的输出。具体的,产生一个上三角矩阵,上三角的值全为0。把这个矩阵作用在每一个序列上,就可以达到目的。
4 Add & Normalize
注意到在经过Multi-Head Attention得到矩阵Z后,并没有直接传入FFN,而是经过了一步:Add & Normalize。
4.1 Add
Add,就是在Z的基础上加了一个残差块X,加入残差块X的目的是为了防止在深度神经网络训练中发生退化问题。
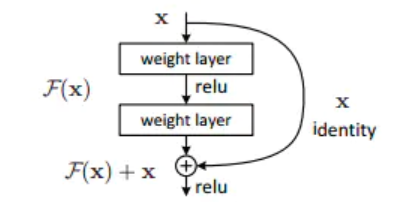
退化的意思就是深度神经网络通过增加网络的层数,Loss逐渐减小,然后趋于稳定达到饱和,然后再继续增加网络层数,Loss反而增大。于是对于多余的层,需要保证他们进行恒等映射,从而不会影响到模型的效果,也就是让 F ( X ) = X F(X)=X F(X)=X。而如果我们加入一个残差块X,如上图,要实现恒等映射 h ( X ) = F ( X ) + X = X h(X)=F(X)+X=X h(X)=F(X)+X=X,只需要实现 F ( X ) = 0 F(X)=0 F(X)=0就可以了。
而构造残差块中使用的ReLU函数能够将负数激活为0,过滤了负数的线性变化,也能够更方便地使得 F ( X ) = 0 F(X)=0 F(X)=0。
4.2 Normalize
归一化能够让神经网络在训练时加快速度和提高稳定性。使用到的归一化方法是Layer Normalization,在同一个样本中不同神经元之间进行归一化。相比于Batch Normalization(在同一个batch中不同样本之间的同一位置的神经元之间进行归一化)而言,LN归一的是样本整体。我们不需要分析每个样本每个维度的输入,因此LN是更合适的。
5 Positional Encoding
在输入的进行Embedding后,要添加一个位置编码,如果不添加位置编码,那么无论单词在什么位置,它的注意力分数都是确定的。
为了理解单词顺序,Transformer为每个输入的词嵌入添加了一个向量,这样能够更好的表达词与词之间的关系。词嵌入与位置编码相加,而不是拼接,他们的效率差不多,但是拼接的话维度会变大。Positional Encoding的公式如下:
{
P
E
(
p
o
s
,
2
i
)
=
sin
(
p
o
s
1000
0
2
i
/
d
m
o
d
e
l
)
P
E
(
p
o
s
,
2
i
+
1
)
=
cos
(
p
o
s
1000
0
2
i
/
d
m
o
d
e
l
)
\begin{cases} PE(pos, 2i) = \sin \left(\frac{pos}{10000^{2i/d_{model}}}\right) \\ PE(pos, 2i + 1) = \cos \left(\frac{pos}{10000^{2i/d_{model}}}\right) \end{cases}
⎩
⎨
⎧PE(pos,2i)=sin(100002i/dmodelpos)PE(pos,2i+1)=cos(100002i/dmodelpos)
其中,pos即position,意为token在句中的位置。设句子长度为L,则
p
o
s
=
0
,
1
,
…
,
L
−
1
pos = 0, 1, \ldots, L - 1
pos=0,1,…,L−1,
i
i
i为向量的某一维度,例如
d
m
o
d
e
l
=
512
d_{model} = 512
dmodel=512时,
i
=
0
,
1
,
…
,
255
i = 0, 1, \ldots, 255
i=0,1,…,255。
6 输出
首先经过一次线性变换(一个简单的全连接神经网络,可以看【神经网络学习日记(2)】全连接神经网络(FCNN)及Pytorch代码实现),然后Softmax得到输出的概率分布,通过词典,输出概率最大的对应的单词作为我们的预测输出。
个人神经网络学习日记:
【神经网络学习日记(1)】神经网络基本概念
【神经网络学习日记(2)】全连接神经网络(FCNN)及Pytorch代码实现
【神经网络学习日记(3)】卷积神经网络(CNN)
【神经网络学习日记(4)】循环神经网络(RNN、LSTM、BiLSTM、GRU)
【神经网络学习日记(5)】数据加载器(DataLoader)的调用
【神经网络学习日记(6)】Transformer结构详解
【神经网络学习日记(7)】Transformer的应用(BERT、Longformer、LLM)
【神经网络学习日记(8)】一些图神经网络的简单介绍(GCN、GAT、rGCN)
文中引用部分都尽可能写出了,如果有侵犯其他人文章版权的问题,请务必联系我,谢谢!
 Transformer结构及注意力机制详解
Transformer结构及注意力机制详解





















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








