mpc原理解释以及代码实现

MPC模型预测控制原理与实现

最新推荐文章于 2025-11-04 16:42:07 发布

原创最新推荐文章于 2025-11-04 16:42:07 发布 · 2.2k 阅读

58 ·

CC 4.0 BY-SA版权

文章标签：

#自动驾驶 #自动化 #线性代数

文章参考B站Dr_can的视频【MPC模型预测控制器】1_最优化控制和基本概念_哔哩哔哩_bilibili

在最优控制中，mpc是一个非常强大的算法，在算力资源充足的情况下，可以在线性/非线性系统中实现对系统的约束，以及预测控制，实用于高精度轨迹跟踪、以及复杂约束系统，广泛应用在自动驾驶领域中。

对比LQR mpc可以对系统进行约束，实现系统输入以及输入的高精度把控。

一.场景分析

比如一辆汽车在路面上行驶，想要变道，如下图所示，采用较为舒缓的路线，动力学上消耗较少。

而如果在紧急避障的情况下，比如前方突然出现一辆汽车，为了躲避，汽车需要紧急向另一车道进行变道，而不考虑舒适度问题。此时在输入能量上比上图消耗更多

二.最优控制和代价函数

在这两种情况下，哪一种是更优控制呢？

显然，图一在考虑舒适角度上更加优秀，而图二在紧急避障上则处理更加迅速，所以，对于不同的应用背景，应当设定不同的指标去衡量优劣，因此我们引入代价函数（Cost Function）的概念：

首先，对于单输入单输出系统（SISO）而言，

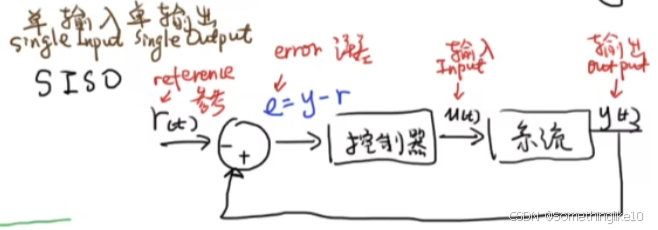
衡量系统性能优劣可以用误差的积累值 $\int_{0}^{t} e^2 dt$ （越小，代表误差越小，收敛越快）和输入的积累值 $\int_{0}^{t} u^2 dt$ （越小，代表控制耗能越少，越节约）来衡量。

由此，我们可以定义代价函数：

$J=\int_{0}^{\infty} qe^2+ru^2 dt$

函数中的q，r分别表示一个增益系数，如果q大，表示希望误差变得更小，收敛更快；r大，表示更注重输入累积，更注重节能。

接下来，我们把其推广到多输入多输出系统（MIMO），使用状态空间描述为：（这里我们假设前馈矩阵为0）

$\dot{X}=AX+BU$ 也就是 $dx/dt = AX + BU$

$Y=CX$

这里x是系统的状态变量，Y是系统的输出量，U为系统的输入量

此时，衡量系统表现优劣就要引入二次型的知识，我们定义：

$J=\int_{0}^{\infty}E^TQE+U^TRUdt$

我们来举一个简单的例子：

$\begin{pmatrix} \dot{x_1} \\ \dot{x_2} \end{pmatrix} =A\begin{pmatrix}x_1 \\ x_2 \end{pmatrix} +B\begin{pmatrix} u_1 \\ u_2 \end{pmatrix}$

为了简化系统，假设输出等于状态变脸

$\begin{pmatrix} y_1 \\y_2 \end{pmatrix} =\begin{pmatrix}x_1 \\ x_2 \end{pmatrix}$

我们假定期望输入是0，那么：

$E =\begin{pmatrix}y_1-r_1 \\ y_2-r_2 \end{pmatrix}=\begin{pmatrix}x_1 \\ x_2 \end{pmatrix}$

$U=\begin{pmatrix}u_1 \\ u_2 \end{pmatrix}$

$E^TQE=\begin{pmatrix}x_1&x_2\end{pmatrix}\begin{pmatrix}q_1&0\\ 0&q_2\end{pmatrix}\begin{pmatrix}x_1 \\ x_2 \end{pmatrix}=q_1x_1^2+q_2x_2^2$

$U^TRU=\begin{pmatrix}u_1&u_2\end{pmatrix}\begin{pmatrix}r_1&0\\ 0&r_2\end{pmatrix}\begin{pmatrix}u_1 \\ u_2 \end{pmatrix}=r_1u_1^2+r_2u_2^2$

这里 E是误差量，Q，R为调节矩阵，q1,q2,r1,r2为权重参数

这里如果只关心x1的追踪情况，就可以将q1设置为一个非常大的数，而将q2设置为一个非常小的数。如果更关心输入（考虑耗能），就可以提高r1以及r2的值如果更关心跟踪性，就可以提高q1，q2的值

也就是说，我们可以通过调节代价函数J的参数，来对系统的最优化提出条件，来趋近于当前条件下的最优控制

三.mpc 模型预测控制的基本概念

通过模型来预测系统在某一个时间段内的表现来进行优化控制

在k时刻，我们可以测量或估计出系统的当前状态y(k)，再通过计算得到的u(k),u(k+1),u(k+2)...u(k+j)得到系统未来状态的估计值y(k+1),y(k+2)...y(k+j)；我们将预测估计的部分称为预测区间（Predictive Horizon）,将控制估计的部分称为控制区间（Control Horizon）

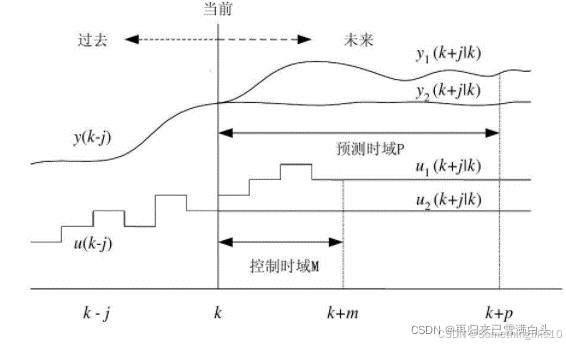
总的步骤：

step1: 估计/测量读取当前系统状态量

step2：基于uk uk+1 ........ uk+n 来进行最优化

离散系统的代价函数可以参考

$J=\sum_{k}^{j-1}E_k^TQE_k+u_k^TRu_k+E_N^TFE_N$ 这里的EN为最终点误差 Terminal Cost 在预测区间最后时刻计算误差的代价函数，对这个代价函数进行最优化

step3：

通过上面的计算，我们可以得到 uk uk+1 uk+3 等控制区间的控制量，但是我们在实际实行输入量时，只输入本时刻计算的uk ,在每一个时间单位都进行预测（求解最优化问题），我们将这样的方案称为滚动优化控制（Receding Horizon Control）。

四.最优化建模

对于mpc而言，有很多中不同方法对其进行最优化，这里介绍较为常用的二次规划（Quadratic Programming）

在一般的离散系统中，形式可以表示为

$x(k+1)=Ax(k)+Bu(k)$

我们定义： $\small u(k|k)$ 是k时刻预测的输入值，而 $\small x(k|k)$ 是k时刻预测的状态值，我们设：

$X_k=\begin{pmatrix}x(k|k) \\ x(k+1|k) \\ x(k+2|k)\\ ...\\ x(k+N|k)\end{pmatrix}$

$U_k=\begin{pmatrix}u(k|k) \\ u(k+1|k) \\ u(k+2|k)\\ ...\\ u(k+N-1|k)\end{pmatrix}$

对于期望输入为0，输出向量等于状态向量的离散系统：

$x(k+1)=Ax(k)+Bu(k)$

$y(k)=x(k)$

$e(k)=y(k)-r(k)=y(k)=x(k)$

我们可以得到代价函数：

$\small J=\sum_{i=0}^{N-1}(x(k+i|k)^TQx(k+i|k)+u(k+i|k)^TRu(k+i|k))+x(k+N)^TFx(k+N)$

其中，我们需要求解的是系统的输入u(k)，这就需要我们把状态项x(k)给消除掉，处理这个事情需要利用系统的状态方程，首先有

$x(k|k)=x(k)$

我们可以通过传感器或者状态估计得到系统当前的状态值，这相当于系统的一个初值，由初值和状态方程可以得到其他项为：

$x(k+1|k)=Ax(k|k)+Bu(k|k)=Ax(k)+Bu(k|k)$

$......$

$x(k+N|k)=A^Nx(k)+A^{N-1}Bu(k|k)+...+Bu(k+N-1|k)$

我们把它简单整理一下，有：

$X_k=\begin{pmatrix}I\\ A\\ A^2\\ ...\\ A^N\end{pmatrix}x(k)+\begin{pmatrix}0&0&...&0\\ B&0&...&0\\ AB&B&...&0\\ ...&...&...&...\\ A^{N-1}B&A^{N-2}B&...&B\end{pmatrix}U_k$

我们再令：

$M=\begin{pmatrix}I\\ A\\ A^2\\ ...\\ A^N\end{pmatrix}$

$C=\begin{pmatrix}0&0&...&0\\ B&0&...&0\\ AB&B&...&0\\ ...&...&...&...\\ A^{N-1}B&A^{N-2}B&...&B\end{pmatrix}$

我们就得到了最简单的形式：

Xk=Mx(k)+CUkXk=Mx(k)+CUk

$\small J=\sum_{i=0}^{N-1}(x(k+i|k)^TQx(k+i|k)+u(k+i|k)^TRu(k+i|k)+x(k+N)^TFx(k+N))\\ =\begin{pmatrix}x(k|k) \\ x(k+1|k) \\ x(k+2|k)\\ ...\\ x(k+N|k)\end{pmatrix}\begin{pmatrix}Q&&&&\\&Q&&&\\&&Q&&\\...&...&...&...&...\\&&&&F\end{pmatrix}\begin{pmatrix}x(k|k) \\ x(k+1|k) \\ x(k+2|k)\\ ...\\ x(k+N|k)\end{pmatrix}^T+U_k^T\begin{pmatrix}R&&&&\\&R&&&\\&&R&&\\...&...&...&...&...\\&&&&R\end{pmatrix}U_k\\$

即：

$J=X_k^T\overline{Q}X_k+U_k^T\overline{R}U_k$

上式还可根据之前推导的公式继续化简，

$\small J=X_k^T\overline{Q}X_k+U_k^T\overline{R}U_k=(x(k)^TM^T+U_k^TC^T)\overline{Q}(Mx(k)+CU_k)+U_k^T\overline{R}U_k\\ \\=x(k)^TM^T\overline{Q}Mx(k)+U_k^TC^T\overline{Q}Mx(k)+x(k)^TM^T\overline{Q}CU_k+U_k^TC^T\overline{Q}CU_k+U_k^T\overline{R}U_k$