自动驾驶-车辆运动学模型

原创已于 2025-08-06 10:02:02 修改 · 2.2k 阅读

42 ·

CC 4.0 BY-SA版权

文章标签：

#自动驾驶 #人工智能 #机器学习

于 2024-12-19 09:17:04 首次发布

文章目录

1、车辆运动学模型
2、一阶转向延迟的车辆运动学模型
参考文献：

1、车辆运动学模型

车辆运动学模型是描述车辆位置、速度和加速度等运动状态的模型，主要关注车辆的位置、速度、前轮转角等的关系，而不考虑任何力的影响。一般考虑运动学模型时，将车辆模型简化成单车模型 (bicycle model) 。

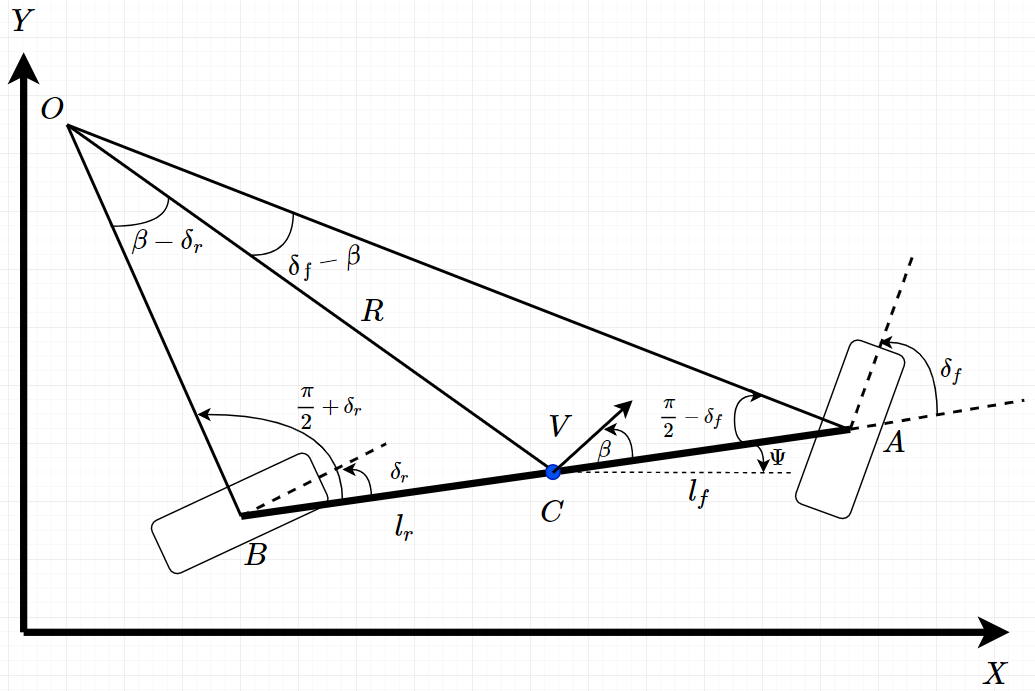
在这里插入图片描述

自行车模型(Bicycle Model)的相关假设条件包括:

不考虑车辆在垂直方向(Z轴方向)的运动，即假设车辆的运动是一个二维平面(X, Y)上的运动。
假设车辆左右侧轮胎在任意时刻都拥有相同的转向角度和转速；车辆左右两个轮胎的运动可以合并为一个轮胎来描述。
假设车辆行驶速度变化缓慢，忽略前后轴载荷的转移。
假设车身和悬架系统都是刚性系统。

单车模型中的符号和定义如下：

$A$ ：前轮中心点； $B$ ：后轮中心点；（左右轮都合并为单个轮子）
$C$ ：车辆重心点；
$\delta _{f}$ ：前轮转向角； $\delta _{r}$ ：后轮转向角；
${l}_{f}$ ：前轮中心点到车辆重心点的距离； ${l}_{r}$ ：后轮中心点到车辆重心点的距离；
$L$ ：车辆轴距， $L={l}_{f}+{l}_{r}$ ；
$V$ ：车辆重心的速度；
$\beta$ ：滑移角，车辆重心速度方向与车辆纵向轴的夹角；
$O$ ：车辆的瞬时旋转中心；
$R$ ：车辆的轨迹半径；
$\Psi$ ：车辆的航向角；

假设速度矢量 $V$ 的方向在 $A$ 点和 $B$ 点的方向与转向角的方向相同，换句话说，在 $A$ 点的速度矢量与车辆纵轴的夹角为 $\delta _{f}$ ，同样 $B$ 点的速度矢量与车辆纵轴的夹角为 $\delta _{r}$ ，也就是说前后轮的滑移角都为 $0$ 。该条件假设成立前提的是车辆速度很低 ( $< 5 m / s$ )，此时轮胎产生的横向力很小，可以忽略。

车辆运动模型基于单车模型推导，推导过程不考虑车辆受到的横向力，故该模型只适用于车辆速度很低的情形。

1.1 运动方程推导

姿态信息 (偏航角)

三角形 $OC A$ 根据正弦定理可得：
$\begin{aligned} \frac{\sin\left ( \delta _{f}-\beta \right )}{{l}_{f}}=\frac{\sin\left ( \frac{\pi }{2}- \delta _{f} \right )}{R} \end{aligned}\tag{1}$
三角形 $OCB$ 根据正弦定理可得：
$\begin{aligned} \frac{\sin\left ( \beta - \delta _{r} \right )}{{l}_{r}}=\frac{\sin\left ( \frac{\pi }{2}+ \delta _{r} \right )}{R} \end{aligned}\tag{2}$
对等式 $(1) 、 (2)$ 分别运用和差定理得：
$\begin{aligned} \frac{\sin \delta _{f} \cos \beta -\cos \delta _{f}\sin \beta }{{l}_{f}}=\frac{ \cos \delta _{f}}{R} \end{aligned}\tag{3}$
$\begin{aligned} \frac{\sin\beta \cos\delta _{r} -\cos\beta \sin \delta _{r} }{{l}_{r}}=\frac{ \cos \delta _{r}}{R} \end{aligned}\tag{4}$
等式 $(3) 、 (4)$ 两边分别同乘 $\frac{{l}_{f}}{\cos \delta _{f}}$ 、 $\frac{{l}_{r}}{\cos \delta _{r}}$ 得：
$\begin{aligned} \tan \delta _{f} \cos \beta -\sin \beta =\frac{{l}_{f}}{R} \end{aligned}\tag{5}$
$\begin{aligned} \sin \beta - \tan \delta _{r} \cos \beta =\frac{{l}_{r}}{R} \end{aligned}\tag{6}$
对等式 $(5) 、 (6)$ 相加得：
$\begin{aligned} \left(\tan \delta _{f} - \tan \delta _{r}\right) \cos \beta=\frac{{l}_{f}+{l}_{r}}{R} \end{aligned}\tag{7}$
根据假设条件，在车辆速度很低时，车辆航向角的变化率 ( $\dot{\Psi}$ ) 可近似等于车辆的角速度 ( $\omega$ )，根据车辆的角速度公式 $\omega = \frac{V}{R}$ ，可得
$\begin{aligned} \dot{\Psi}= \frac{V}{R} \end{aligned}\tag{8}$
将等式(7)带入等式(8)中，消除 $R$ 项得：
$\begin{aligned} \dot{\Psi}= \frac{V\cos \beta}{{l}_{f}+{l}_{r}}\left(\tan \delta _{f} - \tan \delta _{r}\right) \end{aligned}\tag{9}$
等式(9)中共有三个输入变量： $\delta _{f}、\delta _{r}、V$ 。

位置信息

$\begin{aligned} \dot{X} =V\cos \left ( \beta +\Psi \right ) \end{aligned}\tag{10}$
$\begin{aligned} \dot{Y} =V\sin \left ( \beta +\Psi \right ) \end{aligned}\tag{11}$

滑移角 $\beta$ 推导

等式 $(5) 、 (6)$ 两边分别同乘 ${l}_{r}$ 、 ${l}_{f}$ 得：
$\begin{aligned} {l}_{r}\tan \delta _{f} \cos \beta - {l}_{r}\sin \beta =\frac{{l}_{f} \ast {l}_{r}}{R} \end{aligned}\tag{12}$
$\begin{aligned} {l}_{f}\sin \beta - {l}_{f}\tan \delta _{r} \cos \beta =\frac{{l}_{f} \ast {l}_{r}}{R} \end{aligned}\tag{13}$
等式 (12)、(13) 相减得：
$\begin{aligned} \cos \beta \left ( {l}_{f}\tan \delta _{r}+{l}_{r}\tan \delta _{f} \right ) =\left ( {l}_{f} + {l}_{r} \right ) \sin \beta \end{aligned}\tag{14}$
等式 (14) 两端同乘 $\frac{1}{\left ( {l}_{f} + {l}_{r} \right ) \cos \beta}$ 得：
$\begin{aligned} \tan \beta =\frac{ {l}_{f}\tan \delta _{r}+{l}_{r}\tan \delta _{f} }{ {l}_{f} + {l}_{r} } \end{aligned}\tag{15}$
等式 (15) 取反三角函数得：
$\begin{aligned} \beta =\arctan \left (\frac{ {l}_{f}\tan \delta _{r}+{l}_{r}\tan \delta _{f} }{ {l}_{f} + {l}_{r} } \right) \end{aligned}\tag{16}$

微分方程形式

根据等式(9)、(10)、(11)、(16)，对于前轮转向系统， $\delta _{r}=0$ ，可得：
$\begin{aligned} \dot{X} =V\cos \left ( \beta +\Psi \right ) \\ \dot{Y} =V\sin \left ( \beta +\Psi \right ) \\ \dot{\Psi}= \frac{V\cos \beta\tan \delta _{f} }{L} \\ \beta =\arctan \frac{ {l}_{r}\tan \delta _{f} }{ L } \\ \end{aligned}$
当车辆重心点在后轴中心点时， $\beta \cong 0$ ，上述微分方程变为：
$\begin{aligned} \dot{X} =V\cos \Psi \\ \dot{Y} =V\sin \Psi \\ \dot{\Psi}= \frac{V\tan \delta _{f} }{L} \\ \end{aligned}$

1.2 补充-阿克曼转向几何

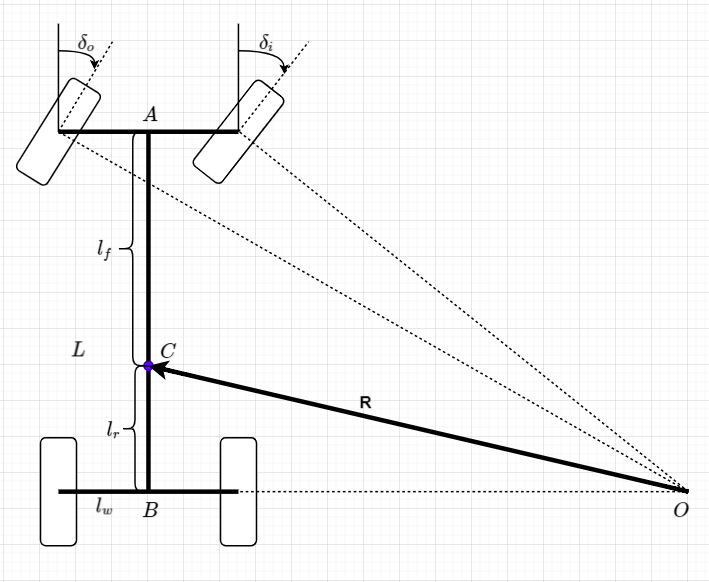
在这里插入图片描述
在单车模型中，假设转向时的左、右前轮偏角为同一角度，但实际两个角度并不完全相等。通常情况下，内侧轮胎转角更大，如上图所示。
上图中， ${l}_w$ 为车轴宽度； $\delta _{o}、\delta _{i}$ 分别表示车辆前轮外侧、内侧转角； $L = {l}_f+{l}_r$ 为车辆轴距，其值远远小于车辆的轨迹半径 $R$ ，滑移角 $\beta$ 接近于 $0$ 。
在车辆后轴为固定轴的情况下， $\delta _{r}=0$ ，等式(9)可以近似为：
$\begin{aligned} \dot{\Psi}= \frac{V\tan \delta _{f} }{L} \end{aligned}\tag{17}$
由于 $\delta _{f}$ 很小，故 $\tan\delta _{f}\approx\delta _{f}$ ，根据等式(8)、(17)可得：
$\begin{aligned} \frac{\dot{\Psi}}{V}\approx \frac{\delta _{f} }{L}=\frac{1}{R} \end{aligned}\tag{18}$
不区分车辆前后轴时，等效转向角为：
$\begin{aligned} \delta= \frac{L}{R} \end{aligned}\tag{19}$
由于内外轮转弯半径不同，根据等式 (19)，车辆外轮转角、内轮转角分别为：
$\begin{aligned} \delta_o= \frac{L}{R+\frac{{l}_w}{2}} \end{aligned}\tag{20}$
$\begin{aligned} \delta_i= \frac{L}{R-\frac{{l}_w}{2}} \end{aligned}\tag{21}$
车辆前轮平均转向角为：
$\begin{aligned} \delta= \frac{\delta_o+\delta_i}{2}= \frac{L}{R-\frac{{l}_w^{2}}{4R}} \end{aligned}\tag{22}$
由于 ${l}_w$ 远远小于 $R$ ，故 $\frac{{l}_w^{2}}{4R}\approx0$ ，等式(22)可近似为：
$\begin{aligned} \delta= \frac{L}{R} \end{aligned}\tag{23}$
车辆内外轮转角之差 $\Delta\delta$ 为：
$\begin{aligned} \Delta\delta= \delta_i-\delta_o= \frac{L\cdot {l}_w}{R^{2}-\frac{ {l}_w^{2}}{4}}\cong \frac{L}{R^{2}}{l}_w=\delta^{2}\frac{{l}_w}{L} \end{aligned}\tag{24}$
根据等式 (24) 可知，前轮内外转向角的差值 $\Delta\delta$ 与平均转向角 $\delta$ 的二次方成正比，所以前轮转向角越大，内外轮的转向角误差就越大。

2、一阶转向延迟的车辆运动学模型

采用以车辆后轴中心为原点的运动学模型
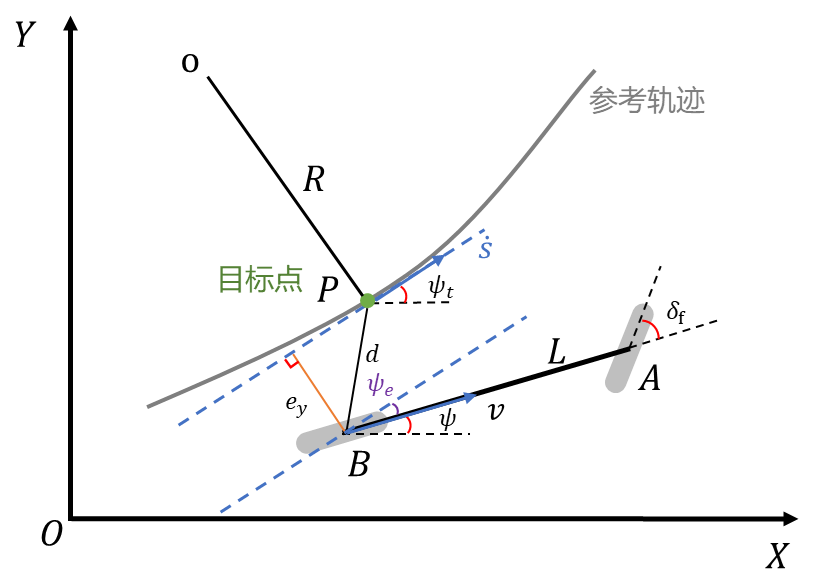
在这里插入图片描述

图中的部分符号和定义如下：
$A 、 B$ ：车辆前轴、后轴中心点；
$P$ ：规划路径中距后轴中心最近的点；
$L$ ：车辆轴距；
$v$ ：车辆后轴中心处的速度；
$\dot s$ ：目标点处的速度；
$\psi$ ：车辆航向角；
$\psi_t$ ： $P$ 点处的航向角；
$\delta_f$ ：车辆的前轮转角；
$\psi_e$ ： $P$ 点处航向角与车辆航向角之间的偏差；
$e_y$ ：前轴中线点到 $P$ 点切线方向的偏差；
$d$ ：后轴中心点到目标点的距离；

其中：
$\begin{aligned} e_y &= d \cdot \sin(\psi_t) \\ \psi_e &= \psi - \psi_t \\ \end{aligned}$
进一步推导可得：
$\begin{aligned} \dot{e}_y &= v \cdot \sin(\psi_e) \\ \dot{\psi}_e &= \frac{v \cdot \tan(\delta_f)}{L} \\ \end{aligned}$
此处在计算 $\dot{\psi}_e$ 时进行了简化，假定 $\dot{\psi}_t=0$ 。

车辆转向一阶延误方程如下：
$\begin{aligned} \tau \cdot \dot{\delta}_f + \delta_f = \delta_d \end{aligned}$
其中， $\delta_d$ 为目标前轮转角， $\tau$ 为转向延迟时间。
上式变化可得：
$\begin{aligned} \dot{\delta}_f = \frac{\delta_d- \delta_f}{\tau} \\ \end{aligned}$
设置状态变量和控制变量如下：
$\begin{aligned} \mathrm{x} &= [e_y, \psi_e, \delta_f]^T \\ \mathrm{u} &= [\delta_d] \end{aligned}$
状态方程如下：
$\begin{aligned} \dot{e}_y &= v \cdot \sin(\psi_e) \\ \dot{\psi}_e &= \frac{v \cdot \tan(\delta_f)}{L} \\ \dot{\delta}_f &= \frac{\delta_d- \delta_f}{\tau} \end{aligned}$
将上述方程利用泰勒方程一阶线性化：
$\begin{aligned} \dot{\mathrm{x}} &= f(\mathrm{x}, \mathrm{u}) \\ \dot{\mathrm{x}} &=f(\mathrm{x_r}, \mathrm{u_r}) + f_\mathrm{x}(\mathrm{x}, \mathrm{u})(\mathrm{x} - \mathrm{x_r})+f_\mathrm{u}(\mathrm{x}, \mathrm{u})(\mathrm{u} - \mathrm{u_r}) \end{aligned}$
其中， $\mathrm{x_r}$ 为参考点处状态量， $\mathrm{u_r}$ 为参考点处控制量。
$\begin{aligned} f_\mathrm{x}(\mathrm{x}, \mathrm{u})& = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \frac{\partial f_1}{\partial x_3} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \frac{\partial f_2}{\partial x_3} \\ \frac{\partial f_3}{\partial x_1} & \frac{\partial f_3}{\partial x_2} & \frac{\partial f_3}{\partial x_3} \end{bmatrix} = \begin{bmatrix} 0 & v \cdot \cos(\psi_e) & 0 \\ 0 & 0 & \frac{v}{L \cdot \cos^{2}(\delta_f)}\\ 0 & 0 & -\frac{1}{\tau} \end{bmatrix} \\ f_\mathrm{u}(\mathrm{x}, \mathrm{u}) &= \begin{bmatrix} \frac{\partial f_1}{\partial u}\\ \frac{\partial f_2}{\partial u}\\ \frac{\partial f_3}{\partial u} \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ \frac{1}{\tau} \end{bmatrix} \end{aligned}$
设参考点处的状态变量和控制变量分别为 $\mathrm{x}_r = [0, 0, \delta_{f_r}]^T$ ， $\mathrm{u}_r = [\delta_{d_r}]$ 可得：
$\begin{aligned} \dot{\mathrm{x}} &= A \cdot \mathrm{x} + B \cdot \mathrm{u} + d\\ A &=\begin{bmatrix} 0 & v_r & 0 \\ 0 & 0 & \frac{v_r}{L \cdot \cos^2(\delta_{f_r})}\\ 0 & 0 & -\frac{1}{\tau} \end{bmatrix} \\ B &= \begin{bmatrix} 0\\ 0\\ \frac{1}{\tau} \end{bmatrix} \\ d &= \begin{bmatrix} 0 \\ -\frac{v_r \cdot \delta_{f_r}}{L \cdot \cos^2(\delta_{f_r})} \\ 0 \end{bmatrix} \\ \end{aligned}$
其中， $v_r$ 为参考点处的速度， $\delta_{f_r}$ 为参考点处的车辆前轮转角。
上式中 $d$ 若基于小角度假设，可以化简为0；但在autoware的运动学模型中， $d$ 为上述值。