2018-06-26 斐波那契数列的一系列恒等式和证明

因为我实在是太菜了，所以所有性质的证明基本上都是数学归纳法。然后这篇博文就变得异常地水。

不过斐波那契这种东西真的是有毒啊......

斐波那契数列的通项公式：

这个的证明很多书上面都有，比如高数书里面的无穷级数里面就会提到这个。（不是我不想写，主要是数学公式编辑器真的，第一次用不熟练啊哭哭）

恒等式一：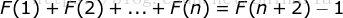

证明：

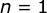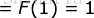当  时，左边  ，右边 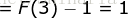 ，因此左边=右边，成立

假设当 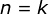 时结论成立，即有  。

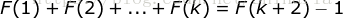当 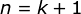 时，即证明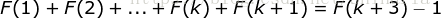 

右边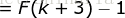 

  

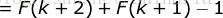
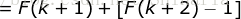
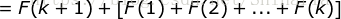  （代入 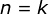时成立的结论）

= 左边，即当 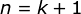 的时候结论也成立。

综上，当 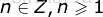 时结论都成立。

恒等式二：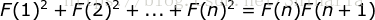

证明：

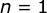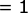当  时，左边  ，右边 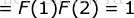 ，因此左边=右边，成立

假设当 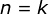 时结论成立，即有  。

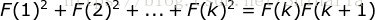当 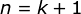 时，即证明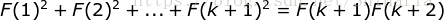 

右边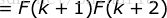 

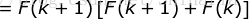
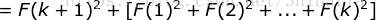
= 左边，即当 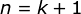 的时候结论也成立。

综上，当 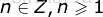 时结论都成立。

恒等式三：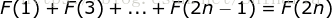

证明：

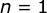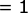当  时，左边  ，右边 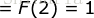 ，因此左边=右边，成立

假设当 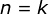 时结论成立，即有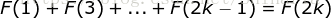 

当 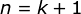 时，即证明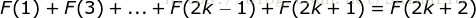 

右边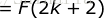 

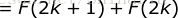
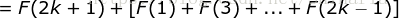
= 左边，即当 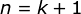 的时候结论也成立。

综上，当 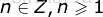 时结论都成立。

恒等式四：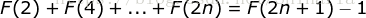

证明：

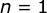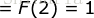当  时，左边  ，右边 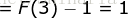 ，因此左边=右边，成立。

假设当 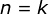 时结论成立，即有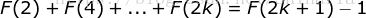 

当 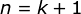 时，即证明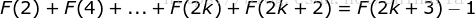 

右边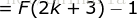 

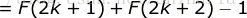
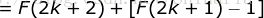
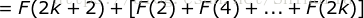
= 左边，即当 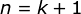 的时候结论也成立。

综上，当 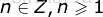 时结论都成立。

恒等式五：给定一个正整数n，任意正整数  都满足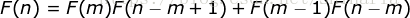  

证明：

当 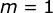 时，原式可以直接写成  ，显然成立。

假设当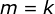 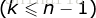  时结论成立，即有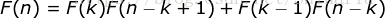

当 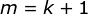 时，即证明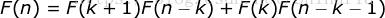 

已有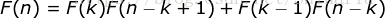

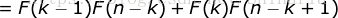
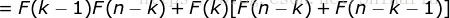
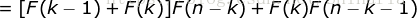
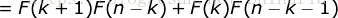
即当 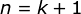 的时候结论也成立。

综上，当 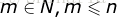 时结论都成立。