CF1041E Tree Reconstruction

最新推荐文章于 2024-01-30 13:52:23 发布

ShadyPi

最新推荐文章于 2024-01-30 13:52:23 发布

阅读量397

点赞数 2

CC 4.0 BY-SA版权

分类专栏： # 构造

本文链接：https://blog.youkuaiyun.com/ShadyPi/article/details/82762533

构造专栏收录该内容

5 篇文章

订阅专栏

本文解析了CodeForces竞赛E题，介绍了一种通过围绕最大节点构建图形的方法来解决树形结构重建的问题。该方法首先确保每条边连接的节点之一具有最大索引值，然后将具有相同最大节点索引的边串联起来形成链，并逐步构建出满足题目要求的树。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原题链接：http://codeforces.com/contest/1041/problem/E

Tree Reconstruction

Monocarp has drawn a tree (an undirected connected acyclic graph) and then has given each vertex an index. All indices are distinct numbers from $1$ to $n$ . For every edge $e$ of this tree, Monocarp has written two numbers: the maximum indices of the vertices of the two components formed if the edge $e$ (and only this edge) is erased from the tree.

Monocarp has given you a list of $n - 1$ pairs of numbers. He wants you to provide an example of a tree that will produce the said list if this tree exists. If such tree does not exist, say so.

Input

The first line contains one integer $n (2 \leq n \leq 1000)$ — the number of vertices in the tree.

Each of the next $n - 1$ lines contains two integers $a_i$ and $b_i$ each $1≤a_i<b_i≤n)$ — the maximal indices of vertices in the components formed if the $i$ -th edge is removed.

Output

If there is no such tree that can produce the given list of pairs, print “NO” (without quotes).

Otherwise print “YES” (without quotes) in the first line and the edges of the tree in the next $n - 1$ lines. Each of the last $n - 1$ lines should contain two integers $x_i$ and $y_i (1≤x_i,y_i≤n)$ — vertices connected by an edge.

Note: The numeration of edges doesn’t matter for this task. Your solution will be considered correct if your tree produces the same pairs as given in the input file (possibly reordered). That means that you can print the edges of the tree you reconstructed in any order.

Examples

input

4
3 4
1 4
3 4

output

YES
1 3
3 2
2 4

input

3
1 3
1 3

output

input

3
1 2
2 3

output

Note

Possible tree from the first example. Dotted lines show edges you need to remove to get appropriate pairs.

题解

每条边一定有一端的最大值为 $n$ ，所以我们就围着 $n$ 建菊花图就好了，左右两端最大值相同的边就串成一条链接在 $n$ 上，样例一构造如下：

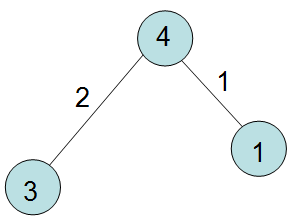
样例中两个 $3\ 4$ 作为一条链， $1\ 4$ 作为单独的一条链，然后中间的点直接贪心从大到小找没有作为端点的点作为中间的点，最后构图如下：

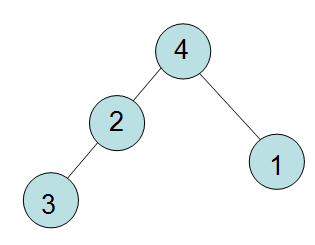
代码

#include<bits/stdc++.h>
using namespace std;
const int M=1005;
struct sd{int a,b;}ed[M];
int n,flag;
vector<int>cot[M];
vector<int>ans[M];
bool vis[M];
void in(){scanf("%d",&n);}
void ac()
{
	int a,b;
	for(int i=1;i<n;++i)
	{
		scanf("%d%d",&a,&b);
		if(i==1&&a==38)flag=1;
		if(a!=n&&b!=n)puts("NO"),exit(0);
		cot[a].push_back(i);cot[b].push_back(i);vis[a]=vis[b]=1;
	}
	for(int i=1;i<n;++i)
	{
		if(!cot[i].size())continue;
		ans[i].push_back(n);
		for(int j=i-1;j>=1;--j)
		{
			if(ans[i].size()==cot[i].size())break;
			if(!vis[j])ans[i].push_back(j),vis[j]=1;
		}
		if(ans[i].size()!=cot[i].size())puts("NO"),exit(0);
		ans[i].push_back(i);
	}
	puts("YES");
	for(int i=1;i<n;++i)if(ans[i].size())for(int j=0;j<cot[i].size();++j)ed[cot[i][j]]=(sd){ans[i][j],ans[i][j+1]};
	for(int i=1;i<n;++i)printf("%d %d\n",ed[i].a,ed[i].b);
}
int main(){in();ac();}