BZOJ3091 城市旅行-优快云博客

本文链接：https://blog.youkuaiyun.com/ShadyPi/article/details/81944102

本文针对城市旅行问题，提出了一种高效的解决方法。通过使用类似高速公路的统计方式，详细阐述了如何处理不同类型的输入操作，并给出了具体的实现代码。适用于1<=N<=50,000的数据规模。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原题链接：https://www.lydsy.com/JudgeOnline/problem.php?id=3091

城市旅行

Description

1(4).jpg

Input

2(3).jpg

Output

3(3).jpg

Sample Input

4 5
1 3 2 5
1 2
1 3
2 4
4 2 4
1 2 4
2 3 4
3 1 4 1
4 1 4

Sample Output

16/3
6/1

HINT

对于所有数据满足 1<=N<=50,000 1<=M<=50,000 1<=Ai<=10^6 1<=D<=100 1<=U,V<=N

题解

可以使用跟高速公路一样的方法来统计每个城市的贡献以及维护方式。

看到网上好多博客都是链到popoqqq大爷那儿的，我简单写一下。

除了最后一个操作，其他三个操作都是基本操作，那么就讲讲最后一个操作。

分母的话，枚举一下起点和终点，就能简单推出，为 $\binom{len+1}{2}$ 。

再考虑一波分子，先统计每个点会贡献多少次，显然，每个点被统计的次数为该点左端的起点数乘以右端的终点数，如下：

考虑如何合并子树信息：

合并前的两棵子树：

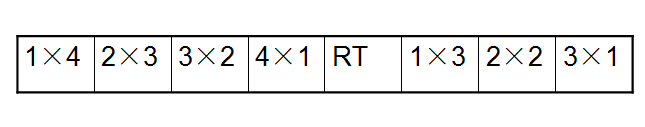
合并后的整条链：

观察系数如何变化，不难发现左子树的系数变化为 $1\times 4,2\times 4,3\times 4,4\times 4$ ，右子树的系数变化为 $5\times 3,5\times 2,5\times 1$ ，根的系数是 $5\times 4$ ，而 $4$ 是右子树的 $s i z + 1$ ， $5$ 是左子树 $s i z + 1$ 。

这样，我们要维护的就是 $le=1\times v_1+2\times v_2+\cdots+n\times v_n$ 和 $ri=n\times v_1+(n-1)\times v_2+\cdots+1\times v_n$ 和 $s i z$ 以及 $s u m$ ，这样答案就呼之欲出了：

$ans[v]=ans[ls]+le[ls]\times (siz[rs]+1)+ans[rs]+ri[rs]\times (siz[ls]+1)+val[v]\times(siz[ls]+1)\times(siz[rs]+1)$

另外，链上加对于 $a n s$ 的贡献是可以直接计算的，有公式：
$1\times n+2\times (n-1)+\cdots+n\times 1=\frac{n\times (n+1)\times(n+2)}{6}$

代码

~~来一发史诗级压行。~~

#include<bits/stdc++.h>
#define ll long long
#define ls son[v][0]
#define rs son[v][1]
using namespace std;
const int M=1e5+5;
int dad[M],son[M][2];
ll le[M],ri[M],sum[M],siz[M],tag[M],ans[M],val[M],n,m;
bool rev[M];
bool notroot(int v){return son[dad[v]][0]==v||son[dad[v]][1]==v;}
void up(int v){siz[v]=siz[ls]+siz[rs]+1,sum[v]=sum[ls]+sum[rs]+val[v],ans[v]=ans[ls]+ans[rs]+le[ls]*(siz[rs]+1)+ri[rs]*(siz[ls]+1)+val[v]*(siz[ls]+1)*(siz[rs]+1),le[v]=le[ls]+val[v]*(siz[ls]+1)+le[rs]+sum[rs]*(siz[ls]+1),ri[v]=ri[rs]+val[v]*(siz[rs]+1)+ri[ls]+sum[ls]*(siz[rs]+1);}
void turn(int v){swap(ls,rs),swap(le[v],ri[v]),rev[v]^=1;}
void add(int v,ll w){tag[v]+=w,sum[v]+=w*siz[v],val[v]+=w,ans[v]+=siz[v]*(siz[v]+1)*(siz[v]+2)/6*w,le[v]+=(siz[v]+1)*siz[v]/2*w,ri[v]+=(siz[v]+1)*siz[v]/2*w;}
void push(int v){if(rev[v]){if(ls)turn(ls);if(rs)turn(rs);rev[v]=0;}if(tag[v]){if(ls)add(ls,tag[v]);if(rs)add(rs,tag[v]);tag[v]=0;}}
void down(int v){if(notroot(v))down(dad[v]);push(v);}
void spin(int v){int f=dad[v],ff=dad[f],k=son[f][1]==v,w=son[v][!k];if(notroot(f))son[ff][son[ff][1]==f]=v;son[v][!k]=f,son[f][k]=w;if(w)dad[w]=f;dad[f]=v,dad[v]=ff;up(f);}
void splay(int v){down(v);for(int f,ff;notroot(v);spin(v)){f=dad[v],ff=dad[f];if(notroot(f))spin((son[f][0]==v)^(son[ff][0]==f)?v:f);}up(v);}
void access(int v){for(int f=0;v;v=dad[f=v])splay(v),rs=f,up(v);}
void beroot(int v){access(v),splay(v),turn(v);}
int root(int v){access(v),splay(v);while(ls)push(v),v=ls;return v;}
void split(int x,int y){beroot(x),access(y),splay(y);}
void link(int x,int y){beroot(x),dad[x]=y;}
void in(){int a,b;scanf("%d%d",&n,&m);for(int i=1;i<=n;++i)scanf("%lld",&val[i]),sum[i]=ans[i]=le[i]=ri[i]=val[i],siz[i]=1;for(int i=1;i<n;++i)scanf("%d%d",&a,&b),link(a,b);}
void ac()
{
	int op,a,b,c;ll u,d,g;
	for(int i=1;i<=m;++i)
	{
		scanf("%d%d%d",&op,&a,&b);
		if(op==1){split(a,b);if(dad[a]==b&&!son[a][1])dad[a]=son[b][0]=0;}
		else if(op==2){beroot(a);if(root(b)!=a)link(a,b);}
		else if(op==3){scanf("%d",&c);split(a,b);if(root(b)==a)add(b,c);}
		else{split(a,b);if(root(b)!=a){puts("-1");continue;}d=siz[b]*(siz[b]+1)/2;g=__gcd(d,ans[b]);printf("%lld/%lld\n",ans[b]/g,d/g);}
	}
}
int main(){in();ac();}