[2018.04.23 T3] 最大值

暂无链接

最大值

【题目描述】

Shy 有 n 个发电站。每个发电站有一个 level（可正可负的整数），i 号发电站的 level要在 l[i],r[i]之间（包含），Level x 会带来 fi(x)的发电量。

Shy 还有 m 个限制。限制是这样的形式，x[u]≤x[v]+d，表示 u 的 level 小于等于 v 的level 加 d（d 是整数）。

请问最大发电量是多少。

【输入】

第一行两个整数 n，m 表示发电站的数目和限制的数目；

接下来 n 行，每行三个整数 ai,bi,ci 表示 fi,fi(x)=ai*x*x+bi*x+ci；

接下来 n 行每行两个整数 l[i],r[i]；

接下来 m 行，每行三个整数 u，v，d，表示 x[u]≤x[v]+d。

【输出】

一个正整数表示答案。

【输入样例】

5 8
1 -8 20
2 -4 0
-1 10 -10
0 1 0
0 -1 1
1 9
1 4
0 10
3 11
7 9
2 1 3
1 2 3
2 3 3
3 2 3
3 4 3
4 3 3
4 5 3
5 4 3

【输出样例】

46

【提示】

【数据规模】

对于 30%的数据，1≤n≤3；

对于 100%的数据，1≤n≤50,0≤m≤100,|ai|≤10,|bi|≤1000,|ci|≤1000, -100≤|li|≤|ri|≤100，1≤u，v≤n，u≠v，|di|≤200。

题解

算是借这道题体会到了网络流的神奇之处，我以前打的都是板子题。。。

这道题可以使用最小割模型，我们将所有发电站的取值范围串起来，边权为$ax^2+bx+c$记作$F(x)$，割掉一条边就相当于选取了这个值，以样例中的前两条边为例，连边如下：

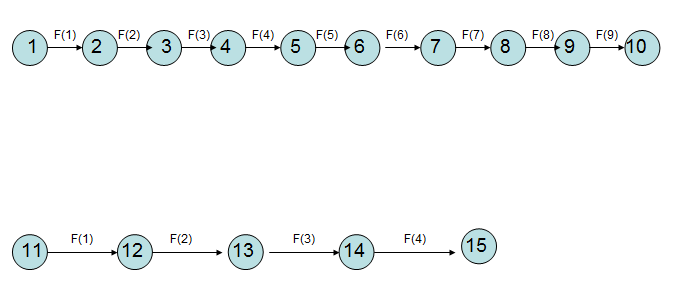
那么最主要的问题在于如何处理限制，对于一个$x[a]\le x[b]+c$，我们需要使割掉了$a$的某个值过后必须割掉比它大$c$的边，且只有仅割掉那条边后为最小割。那么我们可以建图如下：

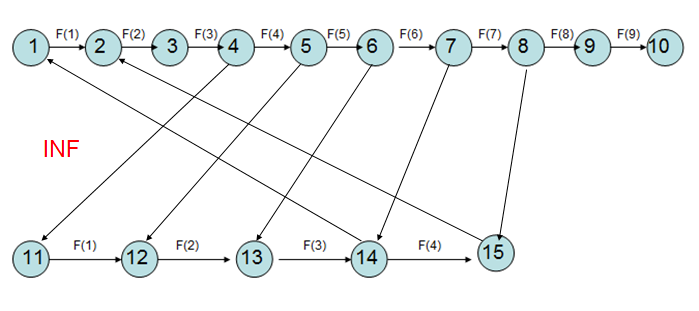
这个图是如何完成上述功能的呢？

例如，对于限制$x[1]\le x[2]+3$，当我们选择割掉1号发电站$F(6)$的边时，我们不能选择割掉2号发电站$F(2)$及以下的边，因为这样仍存在通路，迫使我们割掉其他的边：

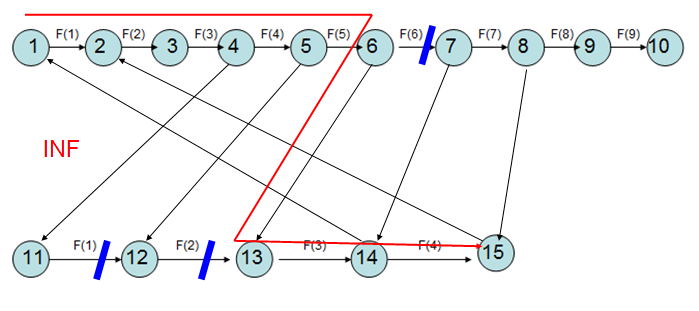
在上图中，割掉$F(1)，F(2)$就是无效的，必须割掉其他的边，而我们求的又是最小割所以我们根本不会割掉$F(1)，F(2)$，中间的边权值又是$INF$根本割不掉，所以最终我们会去割$F(3)$或$F(4)$，这样，我们就成功完成了上述限制。

这个图里面还会有负权的情况，我们只需要在连边时给边权加上一个极大值，因为我们知道我们会割掉$n$条边，我们只需要在输出答案时减回来就行（具体见代码）。

建完图以后连一个超级源点、汇点，跑最小割（最大流）即可$\mathcal{AC}$。

另外，这道题强制加当前弧优化，不然只有$90$分。

代码

#include<bits/stdc++.h>
#define F(i,x) f[i].a*x*x+f[i].b*x+f[i].c
#define R register int
#define I inline
using namespace std;
const int M=1e5+5,N=105,P=19260817,inf=0x3f3f3f3f;
struct edge{int to,fl;};
struct sd{int a,b,c;};
sd f[N];
edge ed[M];
vector<int>mmp[M];
queue<int>dui;
int n,m,id,le[N],ri[N],lb[M],rb[M],lay[M],itr[M],r,fu;
char c;
I int read()
{
    r=0,fu=1;c=getchar();
    while(!isdigit(c)){if(c=='-')fu=-1;c=getchar();}
    while(isdigit(c))r=(r<<1)+(r<<3)+c-'0',c=getchar();
    return r*fu;
}
I void add(int f,int t,int val)
{
    mmp[f].push_back(id);
    ed[id++]=(edge){t,val==inf?inf:P-val};
    mmp[t].push_back(id);
    ed[id++]=(edge){f,0};
}
I bool bfs(int s,int e)
{
    memset(itr,0,sizeof(itr));
    memset(lay,0,sizeof(lay));
    lay[s]=1;dui.push(s);
    R i,f,fl,to,hh;
    while(!dui.empty())
    {
        f=dui.front();dui.pop();
        for(i=mmp[f].size()-1;i>=0;--i)
        {
            hh=mmp[f][i];
            fl=ed[hh].fl;to=ed[hh].to;
            if(lay[to]||!fl)continue;
            lay[to]=lay[f]+1;
            dui.push(to);
        }
    }
    return lay[e];
}
int dfs(int s,int e,int minn)
{
    if(s==e||!minn)return minn;
    int ans=0,tmp,to,fl,hh,siz=mmp[s].size()-1;
    for(int i=itr[s];i<=siz;++i)
    {
        hh=mmp[s][i];
        fl=ed[hh].fl;to=ed[hh].to;
        if(lay[to]!=lay[s]+1||!fl)continue;
        tmp=dfs(to,e,min(fl,minn-ans));
        if(!tmp)continue;
        ed[hh].fl-=tmp;
        ed[hh^1].fl+=tmp;
        ans+=tmp;itr[s]=i;
        if(minn==tmp)break;
    }
    return ans;
}
void in()
{
    R i,j,a,b,c;
    n=read();m=read();
    for(i=1;i<=n;++i)
    f[i].a=read(),f[i].b=read(),f[i].c=read();c=0;
    for(i=1;i<=n;++i)
    {
        le[i]=++c;
        lb[i]=read();rb[i]=read();
        for(j=lb[i];j<=rb[i];++j)
        add(c,c+1,F(i,j)),c++;
        ri[i]=c;
    }
    int x,y,f,t;
    for(i=1;i<=m;++i)
    {
        a=read();b=read();c=read();
        x=lb[a];
        for(j=le[a];j<=ri[a];++j,++x)
        {
            t=x-c;
            if(lb[b]<=t&&t<=rb[b]+1)
            add(j,le[b]+t-lb[b],inf);
        }
    }
    for(i=1;i<=n;++i)
    add(0,le[i],inf),add(ri[i],1e5,inf);
}
void ac()
{
    int ans=0;
    while(bfs(0,1e5))
    ans+=dfs(0,1e5,inf);
    printf("%d",n*P-ans);
}
int main()
{
    in();ac();
    return 0;
}