BZOJ1597 [Usaco2008 Mar] 土地购买

最新推荐文章于 2024-07-12 23:11:17 发布

原创最新推荐文章于 2024-07-12 23:11:17 发布 · 236 阅读

1 ·

CC 4.0 BY-SA版权

动态规划同时被 2 个专栏收录

100 篇文章

订阅专栏

斜率优化

8 篇文章

订阅专栏

本文介绍了一个关于土地购买的算法问题，通过动态规划和斜率优化的方法解决了如何分组购买土地以达到最小总费用的问题。

原题链接：http://www.lydsy.com/JudgeOnline/problem.php?id=1597

土地购买

Description

农夫John准备扩大他的农场,他正在考虑N (1 <= N <= 50,000) 块长方形的土地. 每块土地的长宽满足(1 <= 宽 <= 1,000,000; 1 <= 长<=1,000,000). 每块土地的价格是它的面积,但FJ可以同时购买多快土地. 这些土地的价格是它们最大的长乘以它们最大的宽, 但是土地的长宽不能交换. 如果FJ买一块3x5的地和一块5x3的地,则他需要付5x5=25. FJ希望买下所有的土地,但是他发现分组来买这些土地可以节省经费. 他需要你帮助他找到最小的经费.

Input

第1行: 一个数: N
第2..N+1行: 第i+1行包含两个数,分别为第i块土地的长和宽

Output

第一行: 最小的可行费用.

Sample Input

4
100 1
15 15
20 5
1 100
输入解释:

共有4块土地.

Sample Output

500

FJ分3组买这些土地:

第一组:100x1,

第二组1x100,

第三组20x5 和 15x15 plot.

每组的价格分别为100,100,300, 总共500.

题解

考虑用 $dp[i]$ 表示购买前 $i$ 块土地的最优方案，我们先按照其中一维进行排序，因为当某块土地的长和宽均小于另一块土地时，显然这块土地可以跟另一块土地搭配购买而不用花费任何费用，所以我们再 $O(n)$ 扫描一遍去重。

在剩下的土地中，就会出现这样一维单增一维单减的情况：

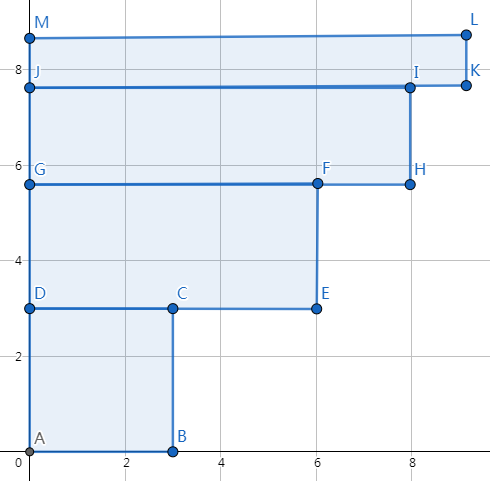
这样在考虑 $i$ 是否与 $j$ $(j<i)$ 搭配购买的时候，最大的宽必定是 $i$ 的，最大的长必定是 $j$ 的。

所以，我们就可以得到状态转移方程如下：

d p [i] = m i n (d p [j] + l a n d [i] . a \times l a n d [j + 1] . b) (j < i)

$dp[i]=min(dp[j]+land[i].a\times land[j+1].b)(j<i)$

接下来，讨论 $k<j<i$ 时， $dp[k]$ 优于 $dp[j]$ 的情况：

dp[k]+land[i].a×land[k+1].b<dp[j]+land[i].a×land[j+1].b d p [ k ] + l a n d [ i ] . a × l a n d [ k + 1 ] . b < d p [ j ] + l a n d [ i ] . a × l a n d [ j + 1 ] . b $dp[k]+land[i].a\times land[k+1].b<dp[j]+land[i].a\times land[j+1].b$

dp[k]−dp[j]<land[i].a(land[j+1].b−land[k+1].b) d p [ k ] − d p [ j ] < l a n d [ i ] . a ( l a n d [ j + 1 ] . b − l a n d [ k + 1 ] . b ) $dp[k]-dp[j]<land[i].a(land[j+1].b-land[k+1].b)$

dp[k]−dp[j]land[j+1].b−land[k+1].b>land[i].a d p [ k ] − d p [ j ] l a n d [ j + 1 ] . b − l a n d [ k + 1 ] . b > l a n d [ i ] . a $\frac{dp[k]-dp[j]}{land[j+1].b-land[k+1].b}>land[i].a$

由于 $land[i].a$ 是个单增的常量，而 $\frac{dp[k]-dp[j]}{land[j+1].b-land[k+1].b}$ 又近似于斜率形式，所以我们可以使用斜率优化。

为了维护斜率单增，我们需要使用单调队列来维护这样一个下凸包，将不符合单调性的点从队列中删去：

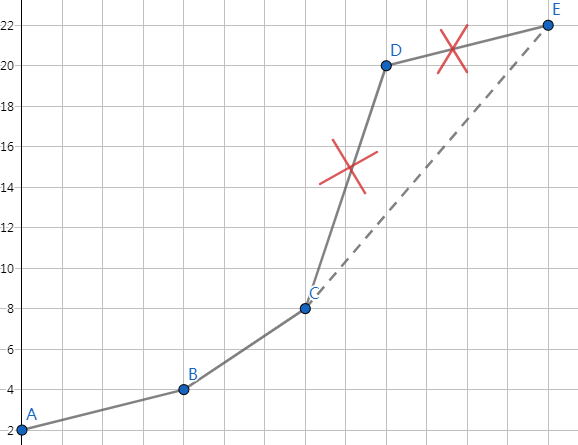
求斜率按照上面推出的公式即可，剩下的就是基础优先队列操作。

代码

#include<bits/stdc++.h>
#define ll long long
#define db double
using namespace std;
const int M=5e4+5;
struct sd{ll a,b;};
sd land[M];
bool operator <(sd a,sd b){return a.a==b.a?a.b<b.b:a.a<b.a;}
int n,que[M];
ll dp[M];
db slop(int a,int b)
{return (dp[b]-dp[a])/(land[a+1].b-land[b+1].b);}
void in()
{
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
    scanf("%d%d",&land[i].a,&land[i].b);
}
void ac()
{
    sort(land+1,land+1+n);
    int cot=0;
    for(int i=1;i<=n;++i)
    {
        while(cot>0&&land[i].b>=land[cot].b)--cot;
        land[++cot]=land[i];
    }
    int le=0,ri=0;
    for(int i=1;i<=cot;++i)
    {
        while(le<ri&&slop(que[le],que[le+1])<land[i].a)le++;
        dp[i]=dp[que[le]]+land[i].a*land[que[le]+1].b;
        while(le<ri&&slop(que[ri],i)<slop(que[ri-1],que[ri]))ri--;
        que[++ri]=i;
    }
    printf("%lld",dp[cot]);
}
int main()
{
    in();ac();
    return 0;
}