POJ1654 Area

原题链接：http://poj.org/problem?id=1654
博主的中文题面：
https://www.luogu.org/problemnew/show/T23040  

Area

Description

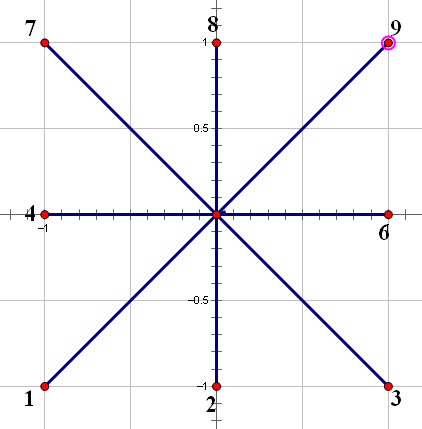
You are going to compute the area of a special kind of polygon. One vertex of the polygon is the origin of the orthogonal coordinate system. From this vertex, you may go step by step to the following vertexes of the polygon until back to the initial vertex. For each step you may go North, West, South or East with step length of 1 unit, or go Northwest, Northeast, Southwest or Southeast with step length of square root of 2.

For example, this is a legal polygon to be computed and its area is 2.5:

Input

The first line of input is an integer t (1 <= t <= 20), the number of the test polygons. Each of the following lines contains a string composed of digits 1-9 describing how the polygon is formed by walking from the origin. Here 8, 2, 6 and 4 represent North, South, East and West, while 9, 7, 3 and 1 denote Northeast, Northwest, Southeast and Southwest respectively. Number 5 only appears at the end of the sequence indicating the stop of walking. You may assume that the input polygon is valid which means that the endpoint is always the start point and the sides of the polygon are not cross to each other.Each line may contain up to 1000000 digits.

Output

For each polygon, print its area on a single line.

Sample Input

4
5
825
6725
6244865

Sample Output

0
0
0.5
2

题解

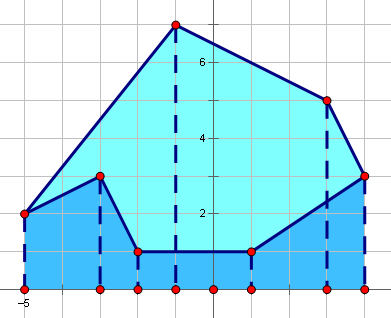
求多边形面积的入门水题，只需要每次计算相邻两点向x轴做垂线所形成的梯形面积（两点与原点连接形成的三角形也可以），由于计算出的面积自带正负，所以累加起来刚好是要求解的多边形面积。

细节

大家可能注意到，当x轴穿过多边形时，上面的结论是错误的，所以我们需要手动将x轴向下平移，这样是不影响结果的。

代码

#include<cstdio>
#include<cstring>
#include<cmath>
#define db double
using namespace std;
struct pt{long long x,y;};
const int M=1e6+5;
const int mod=1e4;
char step[M];
pt p1,p2;
long long area()
{
    if(p1.x==p2.x) return 0;
    return 1ll*(p1.y+p2.y+2*mod)*(p1.x-p2.x)/2;
}
void change(int x)
{
    switch(x)
    {
        case 1:{p2.x-=10;p2.y-=10;break;}
        case 2:{p2.y-=10;break;}
        case 3:{p2.x+=10;p2.y-=10;break;}
        case 4:{p2.x-=10;break;}
        case 6:{p2.x+=10;break;}
        case 7:{p2.x-=10;p2.y+=10;break;}
        case 8:{p2.y+=10;break;}
        case 9:{p2.x+=10;p2.y+=10;break;}
    }
}
void ac()
{
    long long ans=0;
    char p;
    scanf("%s",step);
    int len=strlen(step);
    p1.x=0;p1.y=0;
    p2.x=0;p2.y=0;
    for(int i=0;i<len;++i)
    {
        change(step[i]-'0');
        ans+=area();
        p1=p2;
    }
    ans=ans>0?ans:-ans;
    if(ans%100)printf("%lld.5\n",ans/100);
    else printf("%lld\n",ans/100);
}
int main()
{
    int T;
    scanf("%d",&T);
    for(int i=1;i<=T;++i)
    {
        ac();
    }
    return 0;
}