指数加权平均与其偏差消除_加权平均偏差-优快云博客

本文链接：https://blog.youkuaiyun.com/ShadyPi/article/details/122779725

指数加权平均

对于一个呈序列形式的数据集，一种统计并获得连续曲线的方法是指数加权平均。具体来讲，对于一个数据序列
$\theta_1,\theta_2,\cdots,\theta_m$
如果直接把这些点相连，得到的曲线会包含大量噪声，杂乱而无规律：
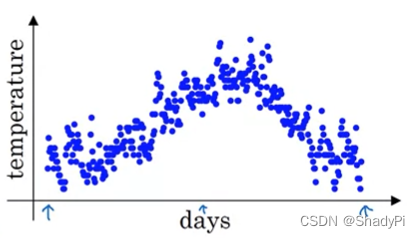
在这里插入图片描述
所以我们重新计算一下每个点的值，令
$v_0=0\\ v_1=\beta v_0+(1-\beta)\theta_1\\ \cdots\\ v_i=\beta v_{i-1}+(1-\beta)\theta_i\\ \cdots\\ v_m=\beta v_{m-1}+(1-\beta)\theta_m\\$
通过该平均方法，我们实际上是对 $1∼i1\sim i$ 的数据进行了加权平均，且权重从 $i$ 到 $1$ 呈指数递减，越靠近当前索引所占的权重越高。一个经验的估计是 $v_i$ 大概代表着前 $11−β\frac{1}{1-\beta}$ 个数据求平均，因为超过该范围的样本所占的权重已经比较小了。

参数 $β\beta$ 影响的就是之前的样本所占权重的衰减速率， $β\beta$ 越接近1，样本权重衰减就越慢，我们囊括的样本就越多，此时曲线会比较平滑，但不能及时反映出当前点产生的效应，通常会比较滞后。而 $KaTeX parse error: Undefined control sequence: \bata at position 1: \̲b̲a̲t̲a̲$ 越接近0，样本权重衰减就越快，曲线就会波动更剧烈，但是对当前数据非常敏感，反应很及时。

下图为 $β=0.9\beta=0.9$ （红色）和 $β=0.98\beta=0.98$ （绿色）时我们得到的曲线：
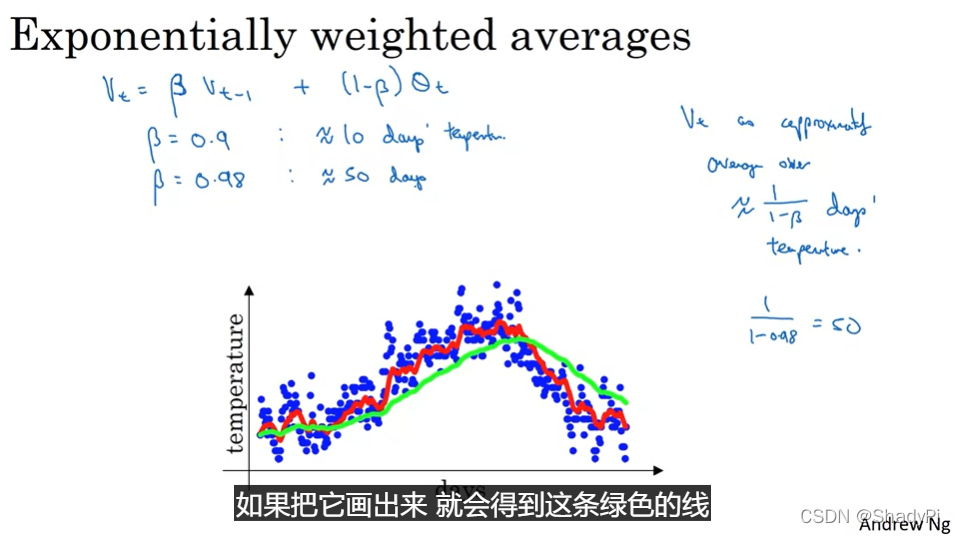
在这里插入图片描述

偏差消除

在实际应用中，我们得到的曲线其实和上图的曲线还有一点偏差，如果 $β=0.98\beta=0.98$ ，我们实际得出的应该是紫色线：
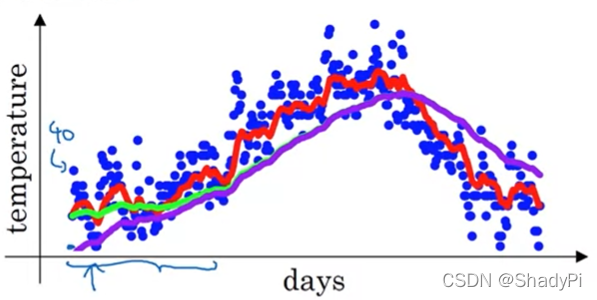
在这里插入图片描述
这是因为在指数加权平均的前期，我们的初始值 $v_0=0$ 还占据了很大的权重，使得曲线的前端都被拉低了，直到曲线的中后程， $v_0$ 的权重衰减的足够低，紫色线才逐渐与绿色线重合。

想要避免这种情况，可以在之前的运算中再加上一项，得到
$v_i=\frac{\beta v_{i-1}+(1-\beta)\theta_i}{1-\beta^i}$
因为初始项 $v_0=0$ 在 $v_i$ 中所占的权重就是 $βi\beta^i$ ，所以除以 $1−βi1-\beta^i$ 就可以排除掉 $v_0$ 带来的影响，得到一个合理的曲线。