机器学习：无监督异常检测算法

总感觉不像机器学习算法。。。像个概率论的高级计算器。

应用场景

异常检测问题指，给定数据集，假定他们都是正常or异常的，当出现一个新样本时，判断该新样本是正常还是异常。通常应用于异常样本极少，且异常原因繁多的情况，在这种情况下，我们没法用监督算法训练出一个模型来进行分类，于是我们更倾向于利用大量正常样本进行无监督训练。

特征值选取

选取一些好的特征值可以让算法事半功倍，在所有特征值中，我们最青睐的是分布看起来就很遵循正态分布的特征值，这一点可以通过绘制直方图（使用hist函数）来观察。如果特征值不太符合正态分布，尽管我们可能依然会得到一个不错的结果，但是加上一些变换将其变为正态分布会使得算法表现得更加优秀。

同时，当算法的检测结果不如人意的时候，我们可以调出判断出错的异常样本，仔细观察它跟别的正常样本有何不同，把最能体现其不同的量作为新的特征值加入算法。

多元正态分布

吴恩达讲的好像都是基于中心极限定理，把特征值的单个分布或者联合分布都看作正态分布，因此就需要用到多元正态分布，尤其是把矩阵用在里面。

众所周知，一元的正态分布p.d.f.是这样的：
$$f(x|\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left[-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right]$$
替换成多元以后，$x$变成了$n\times 1$向量$\vec{x}$，均值也变成$n\times 1$向量$\vec{\mu }$，重要的是这个方差，要变成协方差矩阵$\Sigma$，${\Sigma }_{ij}$就表示$\overrightarrow{x_i}$和$\overrightarrow{x_j}$的协方差。一通操作以后，得到p.d.f：
$$f(\vec{x}|\vec{\mu },\Sigma )=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}\exp \left[-\frac{1}{2}(\vec{x}-\vec{\mu }{)}^T{\Sigma }^{-1}(\vec{x}-\vec{\mu })\right]$$其中$|\Sigma |$表示协方差矩阵$\Sigma$的行列式。

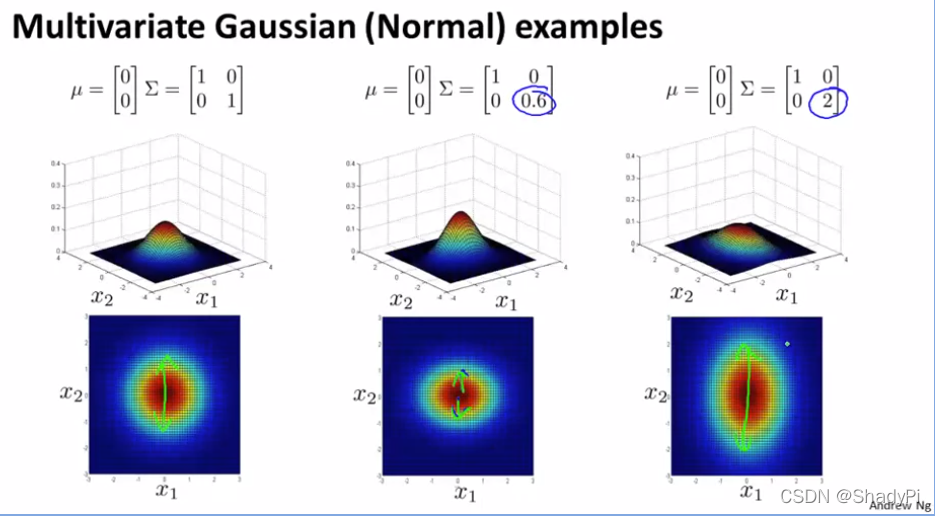
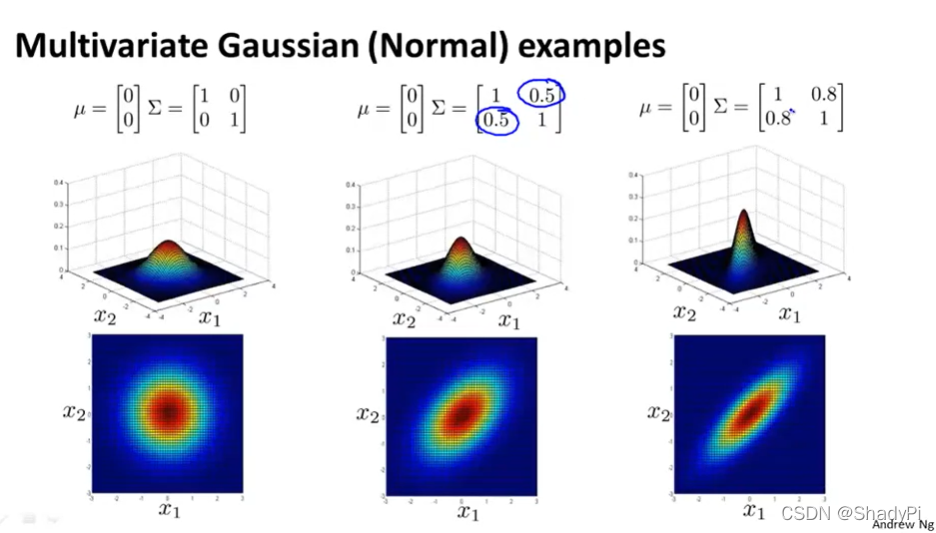
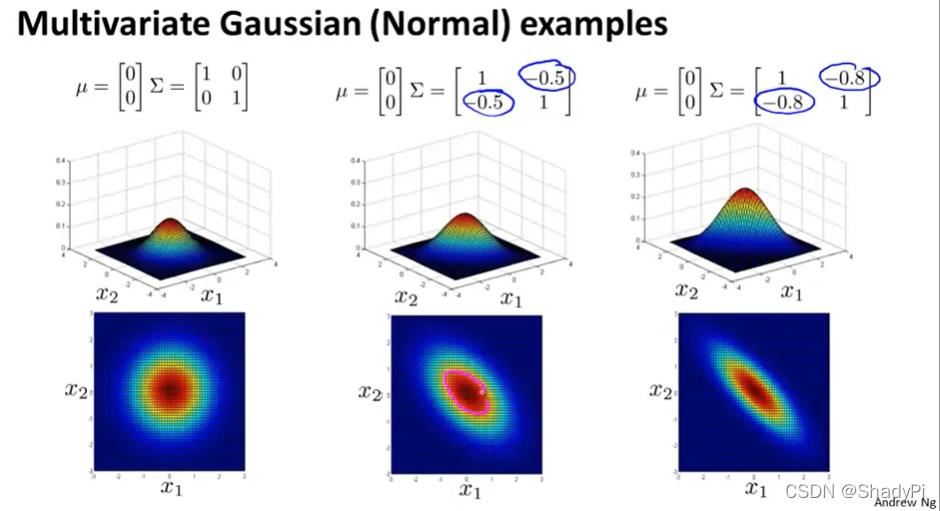
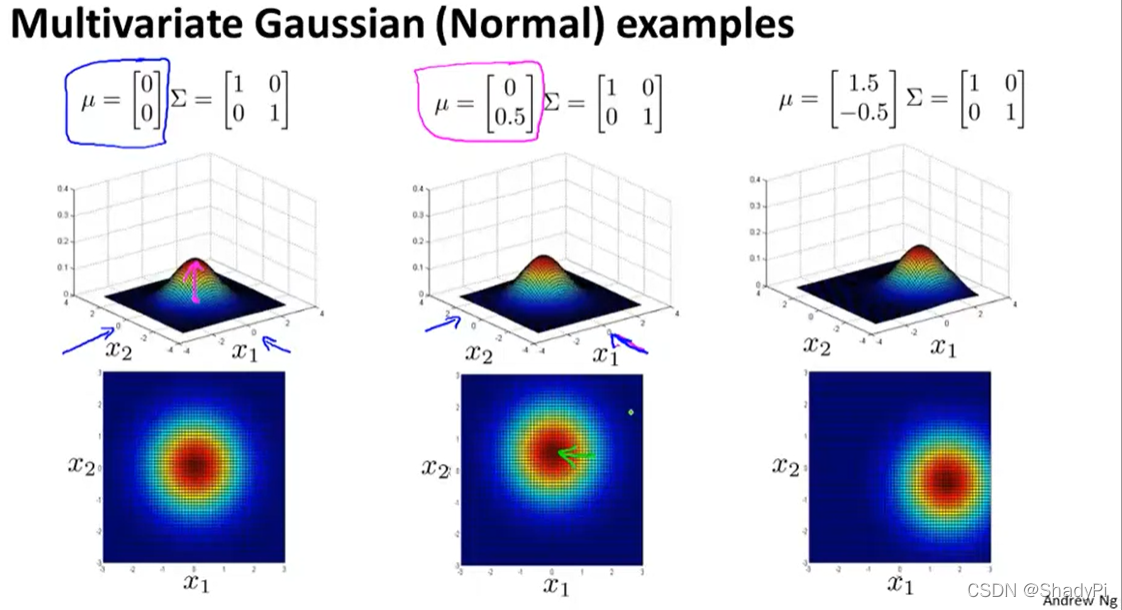
为了更直观地体会$\vec{\mu }$和$\Sigma$的作用，可以参考下面的图像：




同样采用MLE来估计多元正态分布的参数：
$$\begin{gathered} \vec{\mu }=\frac{1}{m}\sum _{i=1}^m{x}^{(i)} \\ \Sigma =\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\vec{\mu })(x^{(i)}-\vec{\mu }{)}^T \end{gathered}$$
这样，当我们向求好参数的模型里输入样本时，若正态分布函数值太小（$<\epsilon$）就认为其是异常点。

当特征值之间有相关性（即某两个特征值协方差不为0）时，使用多元正态分布检测异常正确性更高。如果没有相关性，直接用
$$f(\vec{x}|\vec{\mu },\Sigma )=\prod _{i=1}^{n}f(x_1|{\mu }_1,{\sigma }_1^2)$$是等价的。或者构造新的特征值添加进去，这在$n$很大时非常有效，因为此时多元正态分布的矩阵运算会非常缓慢，尤其是若$m<n$或者有线性相关的特征值，协方差矩阵将不可逆。而在$m>>n$时，多元正态分布比较有效，而且它可以自动捕捉特征值之间的相关性。