首先,使用:=定义一些要用到的常量,:

之后,用Given表示后续给出的是已知信息,列出微分方程:
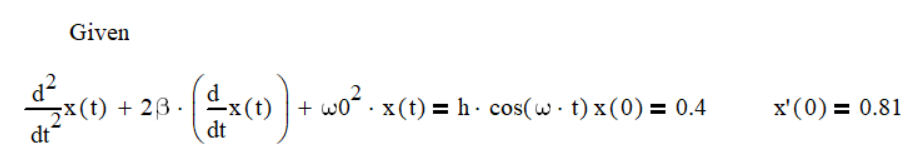
需要注意的是,这里的等号都是布尔等号(加粗的等号)。
再用Odesolve求解,就能得到x(t)x(t)x(t)了,可以在图中形象地展示受迫振动位移与时间的关系:
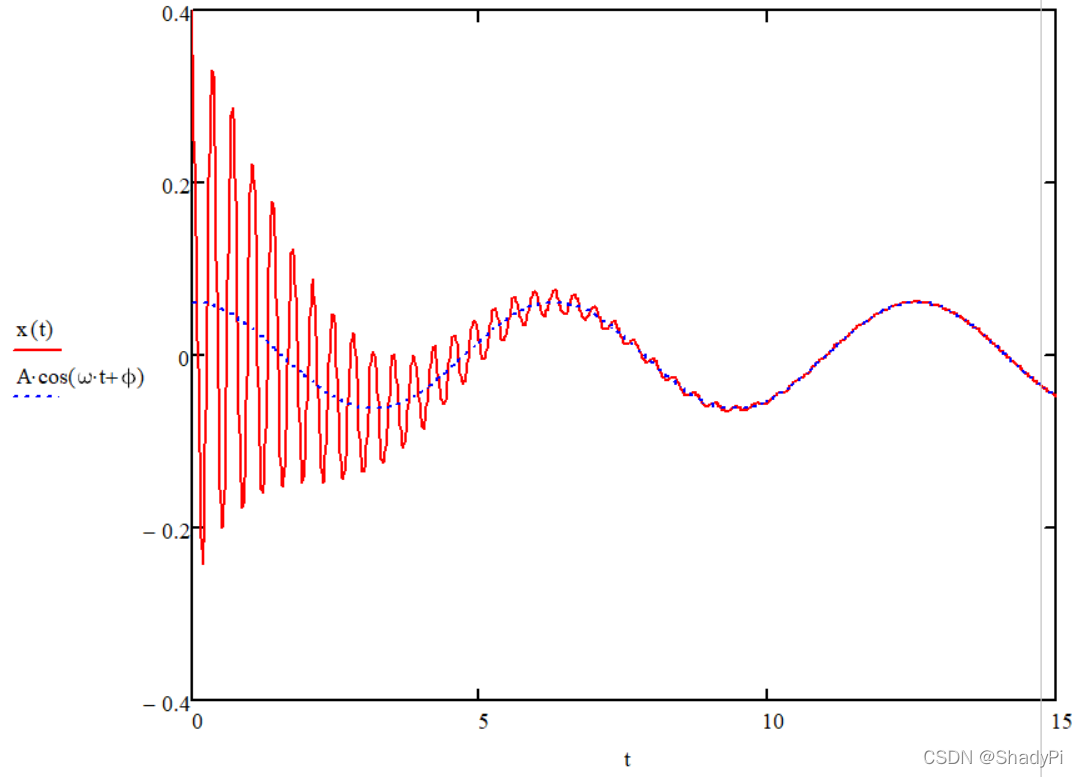
红色实线为所求x(t),蓝色虚线为该受迫振动的稳态解,其中的常量A和\phi定义如下:
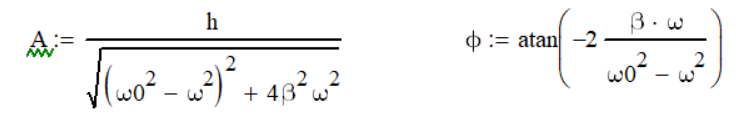
 本文首先定义了所需的常量,并利用Given表示法给出了微分方程。通过使用Odesolve求解器,得到了受迫振动的位移随时间变化的表达式x(t),并展示了其与稳态解之间的关系。
本文首先定义了所需的常量,并利用Given表示法给出了微分方程。通过使用Odesolve求解器,得到了受迫振动的位移随时间变化的表达式x(t),并展示了其与稳态解之间的关系。
首先,使用:=定义一些要用到的常量,:

之后,用Given表示后续给出的是已知信息,列出微分方程:
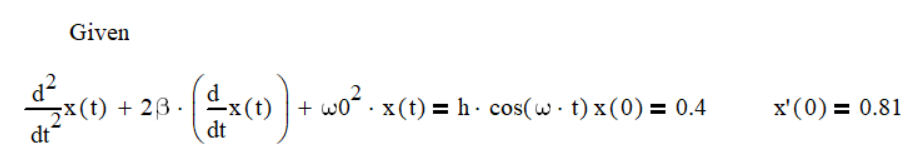
需要注意的是,这里的等号都是布尔等号(加粗的等号)。
再用Odesolve求解,就能得到x(t)x(t)x(t)了,可以在图中形象地展示受迫振动位移与时间的关系:

红色实线为所求x(t),蓝色虚线为该受迫振动的稳态解,其中的常量A和\phi定义如下:
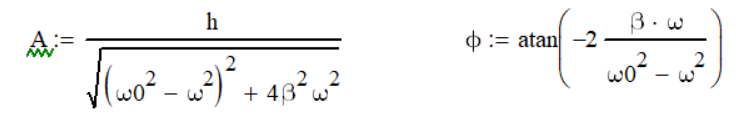
 4576
4576
 1382
1382
 1万+
1万+
 4200
4200