正态分布(normal distribution)又称Gauss分布(Gauss distribution ),是以均数为中心,中间频数分布多,两侧逐渐减少的对称分布,由于频率的总和等于100%或1,故横轴上曲线下的面积等于100%或1。
正态分布曲线的数学函数表达式:

X为连续随机变量,μ为X值的总体均数,σ2 为总体方差,记为X~N(μ,σ2)
(1) 正态分布以均数μ 为中心,左右对称;
(2) 正态曲线(normal curve)在横轴上方,且均数所在处最高,X离μ 越远,f(x)越小,逐渐接近0,但不会等于0,故正态曲线永远不与横轴相交;
(3)正态分布有两个参数,即均数与标准差(m与s)
(4)正态分布的面积分布有一定的规律性,总面积=1;
正态分布的参数
总体均数μ是位置参数:描述正态分布的集中趋势位置。
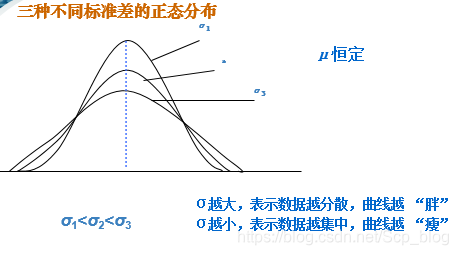
总体标准差σ是变异度参数:描述正态分布离散趋势,越小,分布越集中,曲线形状越“瘦高”;反之越“矮胖”。

标准正态分布(标准正态分布的曲线是唯一的。)

正态分布综述:
1.正态分布是一种很重要的连续型分布,不少的医学现象服从正态分布或近似正态分布,或经变量变换转换为正态分布,可按正态分布规律来处理。它也是许多统计方法的理论基础。
2.正态分布的特征:
(1)曲线在横轴上方,均数处最高
(2)以均数为中心,左右对称
(3)确定正态分布的两个参数是均数μ和标准差σ
3.正态分布常要转换为标准正态分布(N(0,1))使用
4.正态曲线下面积的分布有一定规律。
理论上μ±1σ,μ±1.96σ和μ±2.58σ区间的面积(观察单位数)各占总面积的(总观察单位数)的68.27%,95%和99%,可用来估计医学参考值范围和质量控制等方面。





















 3146
3146

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








