动态规划-最长上升子序列

题目描述

给出一个由 n(n≤5000) 个不超过 10^6106 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。

最长上升子序列是指，从原序列中按顺序取出一些数字排在一起，这些数字是逐渐增大的。

输入格式

第一行，一个整数 n，表示序列长度。

第二行有 n 个整数，表示这个序列。

输出格式

一个整数表示答案。

输入输出样例

输入 

6
1 2 4 1 3 4

输出  

4

遇到动态规划的题目,首先就得画表格

按照题目的意思画一个表格

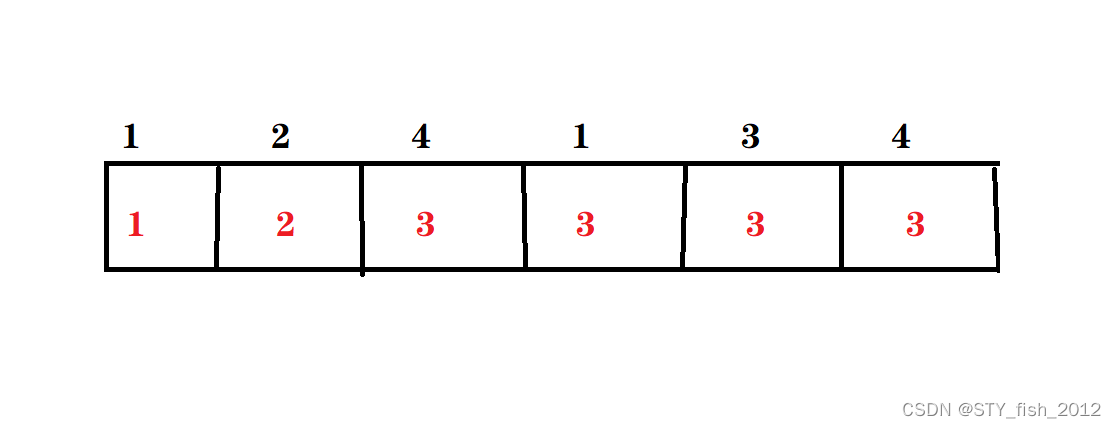
然后就用表格来推状态转移方程

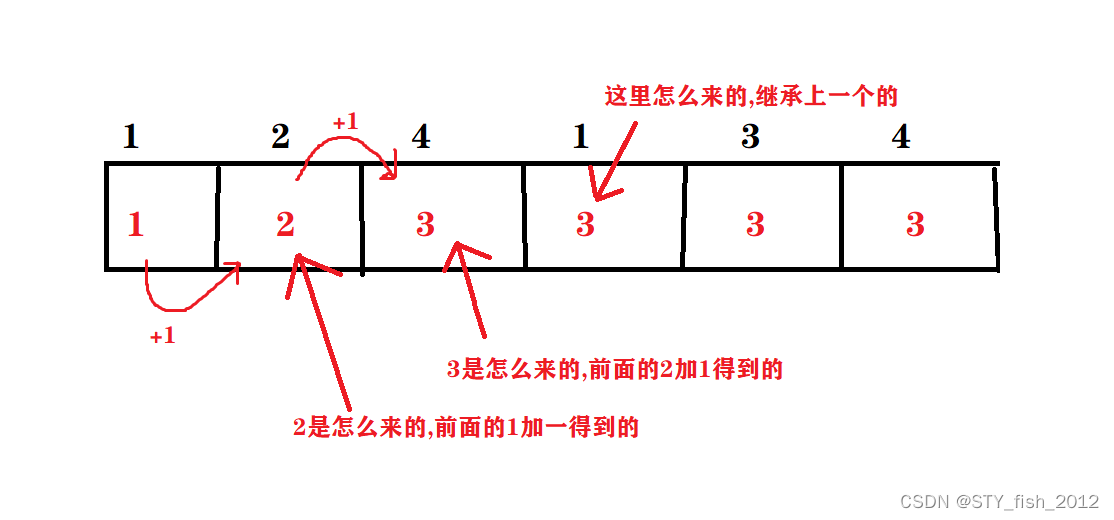
由此,可以推出大致的状态转移方程:

如果比前面的数大,就+1

if(a[i]>a[j])f[i]=max(f[j]+1,f[i]);

代码如下:

#include<bits/stdc++.h>
using namespace std;
int a[5001]={};
int n;
int f[5001]={};
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)
		for(int j=0;j<i;j++)
			if(a[i]>a[j])
				f[i]=max(f[i],f[j]+1);
	int mx=0;
	for(int i=1;i<=n;i++)mx=max(f[i],mx);
	cout<<mx;
	return 0;
}