动态规划-最长上升子序列 (LIS)

最新推荐文章于 2020-04-29 01:35:03 发布

三猪

最新推荐文章于 2020-04-29 01:35:03 发布

阅读量390

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构文章标签：动态规划 LIS

本文链接：https://blog.youkuaiyun.com/weixin_39739342/article/details/88025411

数据结构专栏收录该内容

7 篇文章

订阅专栏

本文通过一个具体实例，详细介绍了如何运用动态规划的思想来求解最长上升子序列问题。通过逐步分解问题，从最简单的子问题开始，逐步构建到复杂的大问题，最终找到整个序列的最长上升子序列。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

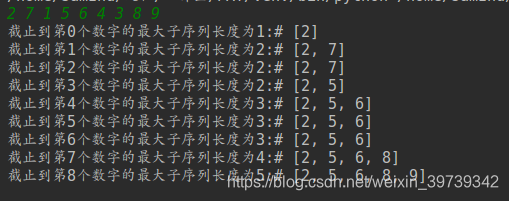
举个例子:求 2 7 1 5 6 4 3 8 9 的最长上升子序列.

动态规划思想:

大问题转化为多个小问题解决,在求最长上升子序列这个问题上,大问题是第i个数的最长上升子序列,小问题是第0到i-1的最长上升子序列,例如上面的例子:

[2] 的最长子序列为 [2]
[2,7] 的最长子序列为 [2,7]
    由于2<7 所以最长子序列等于2的最长子序列+7
[2,7,1] 的最长子序列为 [2,7]
    由于1<2且1<7,所以只能变成一个值的子序列,即[1],但以为序列长度1小于之前出现过的子序列最长,所以等同于之前最长的子序列
同理....

def toint(li):
    for i in range(len(li)):
        li[i]=int(li[i])

a=input()
a=a.split(' ')
toint(a)
vl=[0 for i in range(len(a))]   #存储第i个数字之前的最大子序列长度
result=[[] for i in range(len(a))]  #存储第i个数字之前的最大子序列集

for i in range(len(a)):
    max_num=0
    max_ind=i
    for j in range(i):
        if a[j]<a[i] and vl[j]>max_num:
            #如果第i个数字之前存在比该数字数值更小的数,并寻找符合条件的数中已知的最大的子序列长度最大的数+1,得到第i个数的最大子序列
            max_num=vl[j]
            max_ind=j
    vl[i]=max_num+1
    result[i]=result[max_ind].copy()
    result[i].append(a[i])

key=list(range(len(vl)))
key.reverse()
num=len(vl)
for i in range(num):
    sine=num-1-i
    for j in key[i+1:]:
        if len(result[j])>len(result[sine]):
            result[sine].clear()
            result[sine]=result[j].copy()
            vl[sine]=vl[j]

for i in range(len(result)):
    print('截止到第%d个数字的最大子序列长度为%d:# '%(i,vl[i]),end='')
    print(result[i])