高精度加法

题目描述

高精度加法，相当于 a+b problem，不用考虑负数。

输入格式

分两行输入。a,b \leq 10^{500}a,b≤10500。

输出格式

输出只有一行，代表 a+ba+b 的值。

输入输出样例

输入 1

1
1

输出 1

2

输入 2

1001
9099

输出 2

10100

说明/提示

20% 的测试数据，0≤a,b≤10^9；

40% 的测试数据，0≤a,b≤10^18。

10的18次方肯定是超出了long long的数据范围了,所以说,这道题就要用到高精度

高精度,就是用字符串来存储数,遍历字符串来进行运算

就用这道题来举例

加法,我们就得用字符串来模拟加法竖式

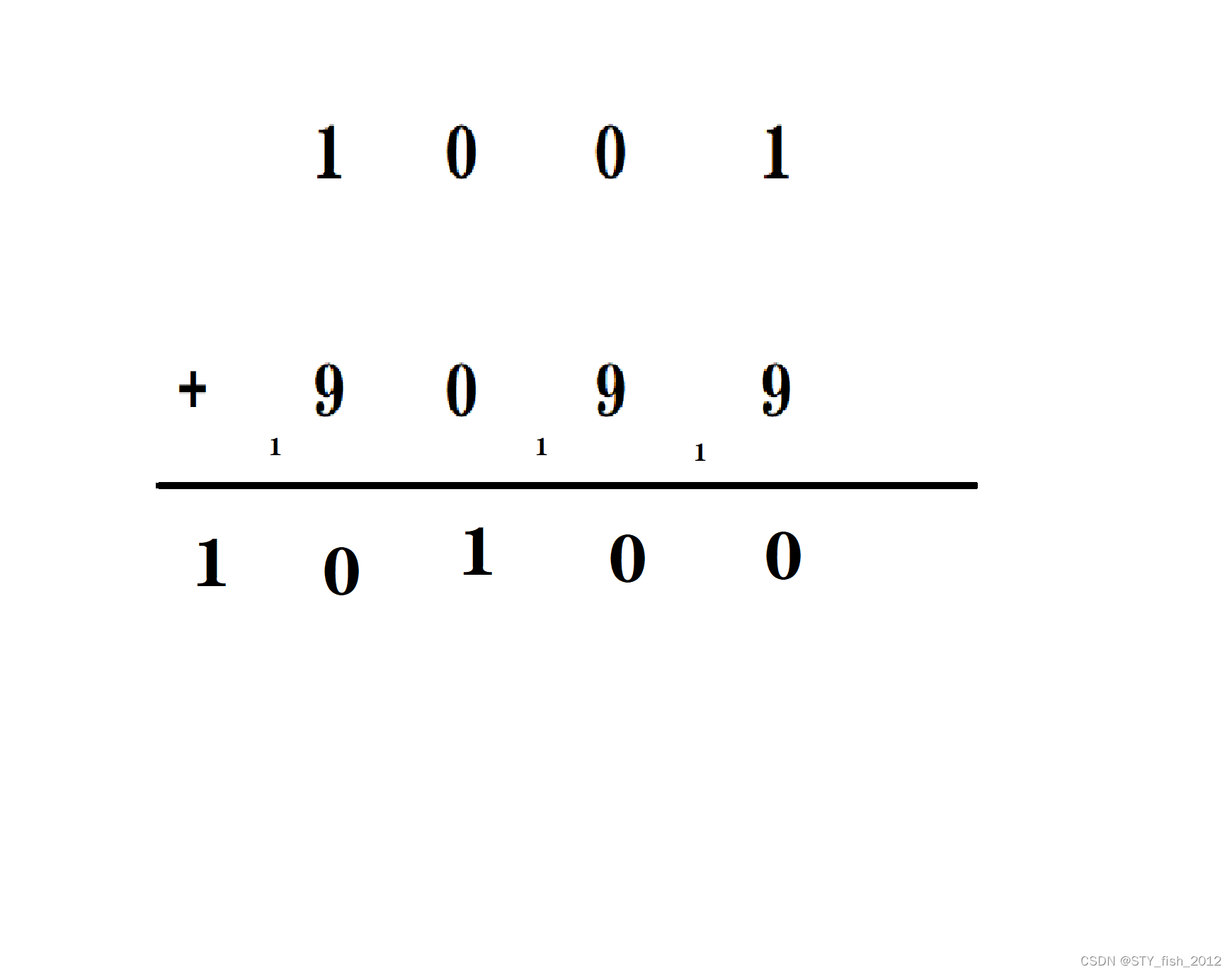
这道题的总体思路是:

输入字符串sa,sb,将字符串里面的每个数存入数组,用数组进行运算

由于加法是从低位到高位进行运算,所以 存入数组是要倒序存放

string sa,sb;
int a[20],b[20];
cin>>sa>>sb;
int la=sa.length();
int lb=sb.length();
for(int i=0;i<la;i++)
	a[la-1-i]=sa[i]-'0';
for(int i=0;i<lb;i++)
	b[lb-1-i]=sb[i]-'0';

 接下来就是运算环节

先定义一个c数组,用来存储运算结果

接着,我们要遍历a,b两个数组,相同位的数相加

中间有非常重要的一步——进位

进位其实非常简单,只需要在当前位数字大于10的时候向下一位进一,将本位减10就行了

if(c[i]>=10){
	c[i]-=10;
	c[i+1]=1;
}

最后输出是要注意:要将c数组倒序输出,以为是把两个数反过来算的

代码如下:

#include<bits/stdc++.h>
using namespace std;
string sa,sb;
int a[1001],b[1001],c[1002];
int main(){
	cin>>sa>>sb;
	int la=sa.length();
	int lb=sb.length();
	for(int i=0;i<la;i++)
		a[la-1-i]=sa[i]-'0';
	for(int i=0;i<lb;i++)
		b[lb-1-i]=sb[i]-'0';
	int lc=max(la,lb);
	for(int i=0;i<lc;i++){
		c[i]=a[i]+b[i]+c[i];
		if(c[i]>=10){
			c[i]-=10;
			c[i+1]=1;
		}
	}
	if(c[lc])lc++;
	for(int i=lc-1;i>=0;i--)cout<<c[i];
 	return 0;
}