【详解】前缀和与差分、树上差分

【例】给定一个n个数的序列为：$a_1,a_2,a_3,...,a_n$，现在询问m次$a_i,a_{i+1},...,a_j$的和。（$1\le n,m\le 10000$）

解决方法：
最直接的方法就是暴力枚举，对于每次询问，使用for(k=i~j)即可计算出答案，时间复杂度为O(N)，m次询问，总时间复杂度为O(MN)。
有没有更快的方法呢？
求解区间和，有一个常用的方法——前缀和。

---

一、前缀和

有一个数组a：a[1]、a[2]、…、a[n]。
前缀和表示数组a某个下标之前所有数的和。

$sum[i]={\sum }_{t=1}^{i}a[t]$

例如：$sum[5]=a[1]+a[2]+a[3]+a[4]+a[5]$
$sum[10]=a[1]+...+a[10]$
当需要求解区间$a[i]+a[i+1]+...+a[j]$时，使用前缀和可以在O(1)的时间求得：
$SUM$ { $a[i]+a[i+1]+..a[j]$ } = $sum[i]-sum[j-1]$
注意，是**$j-1$**。

前缀和是一种预处理的手段，可以极大的降低查询区间和的时间复杂度。

---

二、二维前缀和

有一个二维数组$a[1][1]a[n][m]$，询问矩阵左下角$a[x_1][y_1]$到右上角$a[x_2][y_2]$的和。

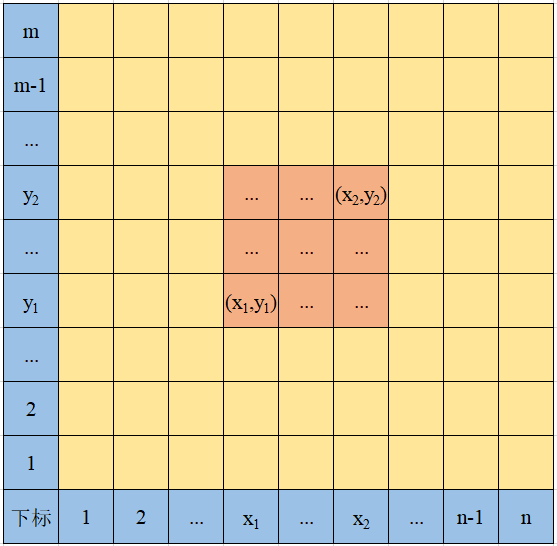
我们仍然可以使用前缀和的方法，但是现在前缀和为$sum[i][j]$，表示矩阵左下角$a[1][1]$到右上角$a[i][j]$的和。
求解矩阵左下角$a[x_1][y_1]$到右上角$a[x_2][y_2]$的和，可以观察下图：

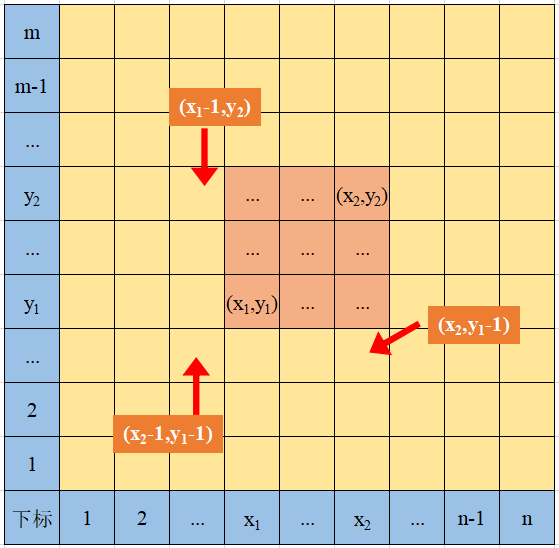
SUM{a[x1][y1] a[x2][y2]}=sum[x2][y2]−sum[x2][y1−1]−sum[x1−1][y2]+sum[x1−1][y1−1]SUM\{a[x_1][y_1] ~ a[x_2][y_2]\}= sum[x_2][y_2] - sum[x_2][y_1-1] - sum[x_1-1][y_2] + sum[x_1-1][y_1-1]SUM{a[x1​][y1​] a[x2​][y2​]}=sum[x2​][y2​]−sum[x2​][y1​−1]−sum[x1​−1][y2​]+sum[x1​−1][y1​−1]

---

三、前缀和局限

可以发现前缀和的使用会预先处理，对于每次询问，可以直接进行调用，在O(1)的时间求得区间和。
但是，如果中途对序列中的元素进行修改，会影响整个前缀和，此时，将不再适用了。而对于这种区间修改，单点修改，可以使用差分。

---

四、差分

差分表示相邻元素的差。
预处理：
$P[i]=A[i]-A[i-1]，i>1$
$P[1]=A[1]，i=1$

差分适用于区间的修改。
现在对区间[x,y]中所有数同时增加一个数Z。实际上，对于差分序列，只有两个端点改变：
$P[x]+=Z，P[y+1]-=Z。$
因为对于中间的数，同时增加，同时减少，差值不变。
差分把对一个区间的操作转化为左、右两个端点的操作，区间修改的时间复杂度为O(1)。

求解修改序列的A[i]：

A[1]=P[1]
A[2]=P[1]+P[2]
A[3]=P[1]+P[2]+P[3]
…
A[n]=P[1]+P[2]+…+P[n]
因此，修改序列的A[i] = 前缀和P[i]。
可以发现，差分序列P的前缀和序列就是原序列A，前缀和序列S的差分序列也是原序列A，所以前缀和与差分是一对互逆运算。

（扩展）
加法和减法，乘法与除法，异或与异或都是一对互逆运算。
乘法与除法：
前缀积：S[i]=A[1] * … * A[i]，A[i]=S[i]/S[i-1]
P[i]=A[i]/A[i-1]（i>1），P[1]=A[1]（i=1）
A[i]=前缀积P[i]

异或与异或：
前缀异或：S[i]=A[1]^A[2]…^{A[i]，A[i]=S[i]}S[i-1]
P[i]=A[i]^A[i-1]（i>1），P[1]=A[1]（i=1）
A[i]=前缀异或P[i]

因此前缀和与差分不光适用于加法和减法，还适用于乘法与除法，异或与异或。

五、典型例题

【FZOJ 2956】【USACO 2016 JAN】Subsequences Summing to Sevens

【题目描述】
给你n个数，分别是a[1],a[2],…,a[n]。求一个最长的区间[x,y]，使得区间中的数(a[x],a[x+1],a[x+2],…,a[y-1],a[y])的和能被7整除。输出区间长度。若没有符合要求的区间，输出0。
【输入格式】
第一行一个数n，接下来为n个数，每个数在0~1000000范围内，1 $\le$ n $\le$ 50000
【输出格式】
输出最大区间长度
【样例输入】
7
3
5
1
6
2
14
10
【样例输出】
5

【分析】
暴力的方式肯定会超时，我们对求解的问题进行分析一下：
（a[x],a[x+1],a[x+2],…,a[y-1],a[y]）% 7=0
那么可以得到：
（（a[1],a[2],a[3],…,a[y-1],a[y]）-（a[1],a[2],…,a[x-2],a[x-1]））% 7=0
所以有：
（a[1],a[2],a[3],…,a[y-1],a[y]）%7 -（a[1],a[2],…,a[x-2],a[x-1]）%7=0
即：
（a[1],a[2],a[3],…,a[y-1],a[y]）%7 =（a[1],a[2],…,a[x-2],a[x-1]）%7
仔细观察，其实就是前缀和：
sum(y)%7=sum(x-1)%7
因此可以得到结论，如果两个前缀和sum(x)和sum(y)能被7整除，则区间[x-1,y]能被7整除。
题目要求最大区间，即求解出前缀和，找出左端第一个整除7的和右端第一个整除7的，就是最大区间。

---

扩展：树上差分

树有这样两个性质：
（1）树上任意两个点的路径唯一。
（2）任何子节点的父亲节点唯一.(可以认为根节点是没有父亲的，或者用0代替)
树上差分可以处理路径修改。

1.点差分

点差分可以统计每个点经过的次数。
$tmp[i]$：表示经过点$i$和$i$的祖先结点的次数。
因此，一个点的经过次数：
$tmp[i]=sum(tmp[v])，v为子节点。$
可以递归求解。

有如下这样一棵树，现在从结点D到结点H：

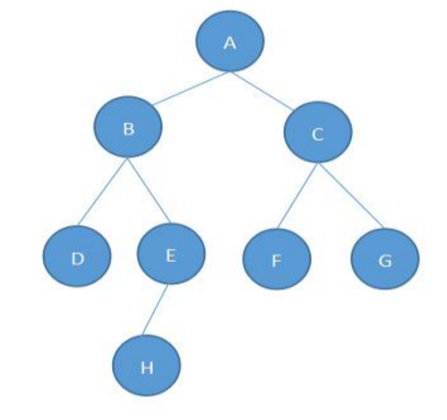
路径D>B->E->H-经过次数都增加1。在这里只需要修改4个结点：

tmp[D]+ +;
tmp[H]+ +;
tmp[B]- -;
tmp[A]- -;

结点D和结点H的增加效果会施加给公共祖先结点$B$，结点$B$只需要增加$1$，但是结点$D$和结点$H$分别给结点$B$施加了1次增加效果，共施加了2次，所有$tmp[B]$需要减$1$，$B$以上的结点不需要增加，所以$tmp[A]$减1，将$tmp[B]$上传的增加效果抵消掉。

因此，如果修改路径$x$->$y$，则：

tmp[x]++;
tmp[y]++;
tmp[lca(x,y)]- -;
tmp[f[lca(x,y)][0]]- -;//（f[u][i]表示u向上走2^i步到达的结点，f[u][0]为lca的父亲结点）

求所有点的经过次数，使用递归求解。

void dfs(int u,int father)
{
	for(int i=first[u];i!=-1;i=nex[i])
	{
		int v=to[i];
		if(v==father) continue;
		dfs(v,u);
		tmp[u]+=tmp[v];
	}
}

2.边差分

边差分统计每条边经过的次数。

$tmp[i]$：表示的是$i$到其父亲的边的次数和到根结点路径上的边的次数。
如上图，如果从结点D到结点H：

tmp[D]++;
tmp[H]++;
tmp[B]-=2;

结点$B$到父亲的边未经过，而$D$和$H$分别给了$1$次增加效果，所以减2抵消增加效果。
因此，如果修改路径$x->y$，只需要 ：

tmp[x]++;
tmp[y]++;
tmp[lca(x,y)]-=2;

3.练习

【JLOI 2014】松鼠的新家（点差分）
【POJ 3417】暗的连锁（边差分）