小X的矩阵

题目描述

小X最近迷上了矩阵，他定义了一个对于一种特殊矩阵的特征函数G。对于N*N的矩阵A，A的所有元素均为0或1，则G(A)等于所有A[i][j]*A[j][i]的和对2取余之后的结果。举一个例子：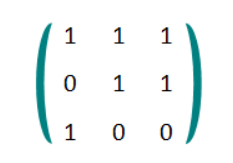

对于上图这个33矩阵A，G(A)=(11+10+11+01+11+10+11+ 01+00) mod 2=0
当然询问一个矩阵的G值实在是太简单了。小X在给出一个N*N矩阵的同时将给你Q个操作，操作描述如下：
操作1：形如一个整数1和一个整数x，表示将第x行的元素全部“翻转”。
操作2：形如一个整数2和一个整数x，表示将第x列的元素全部“翻转”。
操作3：形如一个整数3，表示询问当前矩阵的特征值G。
“翻转”的定义为将1变成0，将0变成1。

输入

第1行：两个正整数N，Q。 N表示矩阵的行数(列数)，Q表示询问的个数。
接下来N行：一个N*N的矩阵A，0<=A[i][j]<=1。
接下来Q行：Q个操作。

输出

一行若干个数，中间没有空格，分别表示每个操作的结果（操作1和操作2不需要输出）。

输入样例

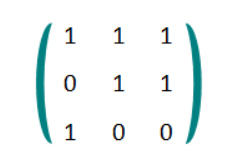
3 12
1 1 1
0 1 1
1 0 0
3
2 3
3
2 2
2 2
1 3
3
3
1 2
2 1
1 1
3

输出样例

01001

思路

非常简单

题目规定了$Ans=(i,j)\ast (j,i)+\dots \dots$
因为$1<=i<=n$且$1<=j<=n$
可以得知$(i,j)\ast (j,i)$加了两次
所以可以直接变成$\ast 2$
假设$(i,j)=0$或$(j,i)=0$那么$(i,j)\ast (j,i)\ast 2$%$2=0$
如果$(i,j)=(j,i)=1$那么$(i,j)\ast (j,i)\ast 2$%$2=0$
所以有些计算是没有用的
但是正方形对角线不收影响
$(i,i)\ast (i,i)\ast 2$
如果是$1$就$1$
如果是$0$就$0$
然后翻转的时候
无论是行还是列
都只能改变对角线上的一个数
所以只要有翻转时
直接$Ans=(Ans+1)$%$2$

#include<iostream>
#include<cstdio>
using namespace std;
int Operation,Ans,k,n,m;
int Matrix[1025][1025];
void Sum()
{
	Ans=0;
	for(int i=1;i<=n;++i)//只算对角线上的
		Ans=(Ans+Matrix[i][i])%2;
	return;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i)
		for(int j=1;j<=n;++j)
			scanf("%d",&Matrix[i][j]);
	Sum();//先算出一开始的
	for(int i=1;i<=m;++i)
	{
		scanf("%d",&Operation);
		switch (Operation)
		{
			case 1:{scanf("%d",&k);Ans=(Ans+1)%2;break;}
			case 2:{scanf("%d",&k);Ans=(Ans+1)%2;break;}//见上
			case 3:{printf("%d",Ans);break;}
		}
	}
	return 0;
}