矩阵的投影、线性拟合与最小二乘法

概要：投影矩阵

        

      如果一个b向量进行矩阵运算  Pb  , 那么向量b就会投影要A的列空间的最近点。

       

目录

一、矩阵的四大基础子空间

二、投影矩阵

三、最小二乘法

---

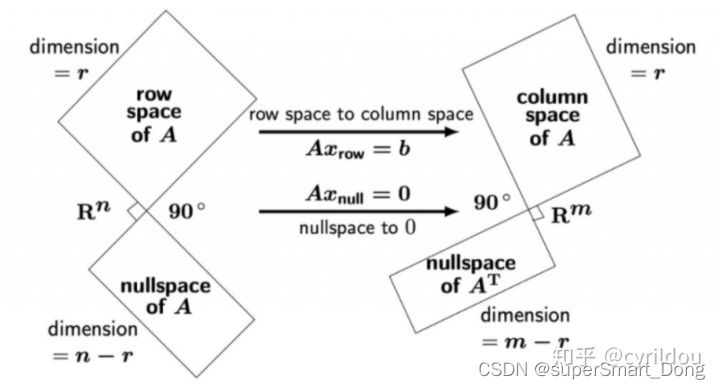
一、矩阵的四大基础子空间

        一个矩阵有4个子空间。分别是行空间、零空间、列空间和左零空间(A转置的零空间).所谓A矩阵的行空间就是矩阵的行向量的线性组合，它与零空间正交(即向量垂直，内积为0)。A矩阵的列空间就是矩阵列向量的线性组合，它与左零空间正交。

对于一个初等矩阵E，如果满足 EA=B,那么B的每个行向量都是A行向量的线性组合,A的行向量也是B行向量的线性组合，即A和B的行空间是一样的，并且Ax=0 与 Bx=0的解也是相同的,即A与B的零空间相同。同理，如果AE=B那么A与B有相同的列空间和左零空间。

 零空间该如何求出来的，最简单的就是化成最简式

例如 存在一个初等矩阵E，化成最简式EA=R， 

A，R拥有相同的行空间，即每行都是 (1,2,3)与(4,5,6)的线性组合，同时也是(1,0,-1)与(0,1,2)的线性组合。