题目描述
定义f(x)f(x)f(x)为xxx的约数个数,xxx为正整数。
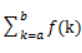
=f(a)+f(a+1)+……+f(b)=f(a)+f(a+1)+……+f(b)=f(a)+f(a+1)+……+f(b),即aaa,bbb之间每个数的约数的总和。
输入
一行两个正整数aaa、bbb,以一个空格隔开。
输出
一行一个整数,即答案。
输入样例
2 6
输出样例
13
说明
【数据范围】
对于505050%的数据,1≤a≤b≤10001≤a≤b≤10001≤a≤b≤1000;
对于100100100%的数据,1≤a≤b≤10,000,0001≤a≤b≤10,000,0001≤a≤b≤10,000,000。
思路
本题采用前缀和思想
求出mmm和n−1n-1n−1的因数和
因为是前缀和,nnn也要算进去,所以是n−1n-1n−1
然后m−nm-nm−n就行了
#include<iostream>
#include<cstdio>
using namespace std;
int n,m,x,y;
int main()
{
scanf("%d %d",&n,&m);
n--;
for(int i=1;i<=n;++i)
x+=n/i;
for(int i=1;i<=m;++i)
y+=m/i;
printf("%d",y-x);
return 0;
}







 本文介绍了一种计算两个正整数间所有数的约数总和的算法,利用前缀和思想,通过计算两个边界值的约数和并相减得到结果。适用于数据范围内的快速求解。
本文介绍了一种计算两个正整数间所有数的约数总和的算法,利用前缀和思想,通过计算两个边界值的约数和并相减得到结果。适用于数据范围内的快速求解。
















 456
456

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








