【SHTSC2013】超级跳马(矩阵快速幂)

最新推荐文章于 2021-06-23 07:18:19 发布

原创最新推荐文章于 2021-06-23 07:18:19 发布 · 293 阅读

1 ·

CC 4.0 BY-SA版权

c++ 同时被 3 个专栏收录

372 篇文章

订阅专栏

jzoj比赛

206 篇文章

订阅专栏

动态规划

119 篇文章

订阅专栏

本文深入探讨了棋盘上特定跳跃路径的计数问题，通过矩阵快速幂算法优化求解，针对不同数据规模提出90分及100分解决方案，适用于竞赛编程中的动态规划与图论挑战。

Description
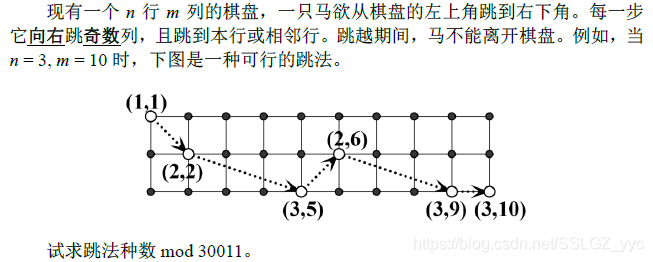
在这里插入图片描述

Input
仅有一行，包含两个正整数n, m，表示棋盘的规模。

Output
仅有一行，包含一个整数，即跳法种数mod 30011。

Sample Input
3 5

Sample Output
10

Data Constraint
对于10%的数据，1 ≤ n ≤ 10，2 ≤ m ≤ 10；
对于50%的数据，1 ≤ n ≤ 10，2 ≤ m ≤ 10^5；
对于80%的数据，1 ≤ n ≤ 10，2 ≤ m ≤ 10^9；
对于100%的数据，1 ≤ n ≤ 50，2 ≤ m ≤ 10^9。

.
.
.
.
.
分析
90分：
做一个3*n的矩阵，前n列表示距离下一行为奇数的每一列的答案的和，中间n列代表偶数的，最后n列代表最后一列的答案
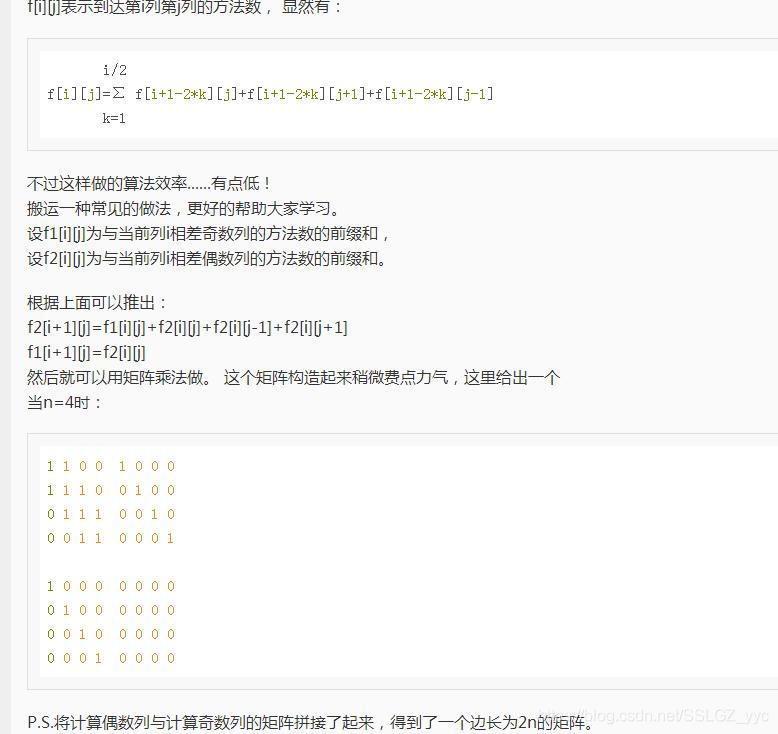
在这里插入图片描述

100分：
换一种构图
在这里插入图片描述

.
.
.
.
.
程序(90分)：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int n,m,ansjz[155][155],jz[155][155],t[155][155],mo=30011;

void jzksm(int a[155][155],int b[155][155])
{
    memset(t,0,sizeof(t));
    for (int i=1;i<=3*n;i++)
        for (int j=1;j<=3*n;j++)
			for (int k=1;k<=3*n;k++)
				t[i][j]=(t[i][j]+(a[i][k]*b[k][j]%mo))%mo;
				
	for (int i=1;i<=3*n;i++)
    	for (int j=1;j<=3*n;j++)
			a[i][j]=t[i][j];
}

void work()
{
	for (int i=1;i<=n;i++)
	{
        jz[2*n+i][i]=1;
        if (i-1>=1)
		{
            jz[i-1][n+i]=1;
			jz[n+i-1][n+i]=1;
        }
		jz[i][n+i]=1;
		jz[n+i][n+i]=1;
		jz[i][2*n+i]=1;
		jz[n+i][2*n+i]=1;
        if (i+1<=n)
		{
            jz[i+1][n+i]=1;
            jz[n+i+1][n+i]=1;
        }
    }
    ansjz[1][n+1]=1;
}

int main()
{
	scanf("%d%d",&n,&m);
	if (m==1)
	{
		if (n==1) cout<<1; else cout<<0;
		return 0;
	}
    work();
    m--;
    while (m!=0)
	{
        if (m&1) jzksm(ansjz,jz);
        m>>=1;
        jzksm(jz,jz);
    }
    printf("%d",ansjz[1][2*n]);
    return 0;
}

.
.
.
.
.
.
程序(100分)：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int n,m,mo=30011,t[200][200],b[200][200],a[200][200],jz[200][200];

void jzksm(int a1[200][200],int b1[200][200])
{
    memset(t,0,sizeof(t));
    for (int i=1;i<=2*n;i++)
        for (int j=1;j<=2*n;j++)
            for (int k=1;k<=2*n;k++)
                t[i][j]=(t[i][j]+a1[i][k]*b1[k][j])%mo;
    for (int i=1;i<=2*n;i++)
        for (int j=1;j<=2*n;j++)
            a1[i][j]=t[i][j];
}

void work()
{
    for (int i=1;i<=n;i++)
    {
    	if (i+1<=n) jz[i+1][i]=jz[i][i+1]=1;
    	jz[i][i]=jz[i+n][i]=jz[i][i+n]=1;
	}
    
    for (int i=1;i<=2*n;i++)
        for (int j=1;j<=2*n;j++)
            a[i][j]=b[i][j]=jz[i][j];
    
    memset(t,0,sizeof(t));
    m-=3;
}

int main()
{
    scanf("%d%d",&n,&m);
    if (m==1)
	{
		if (n==1) cout<<1; else cout<<0;
		return 0;
	}
	work();
    while (m!=0)
    {
        if (m&1) jzksm(b,jz);
        m>>=1;
        jzksm(jz,jz);
	}
    jzksm(a,b);
    printf("%d",((long long)a[1][n]-b[1][2*n]+mo)%mo);
    return 0;
}