AHP与FAHP：权重决策的双生花，SPSSAU智能分析全解析

在复杂的决策分析中，如何科学地确定各指标权重一直是研究者面临的挑战。层次分析法(AHP)及其模糊扩展(FAHP)作为两种经典的权重计算方法，在学术研究和商业分析中广泛应用。本文将深入解析这两种方法的原理、流程及应用，帮助读者全面理解权重分析的精髓。

一、AHP层次分析法：清晰的层次决策框架

1.1 AHP分析流程全解析

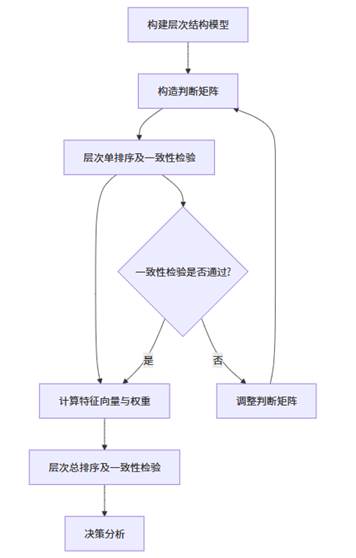
AHP层次分析法的核心在于将复杂问题分解为多个层次和因素，通过两两比较的方式确定各因素的相对重要性。上图清晰地展示了AHP分析的完整流程：从构建层次结构开始，到构造判断矩阵，接着进行一致性检验确保逻辑合理性，最后计算权重并进行决策分析。整个过程环环相扣，确保权重计算的科学性和可靠性。

1.2 AHP核心表格解析

（1）判断矩阵

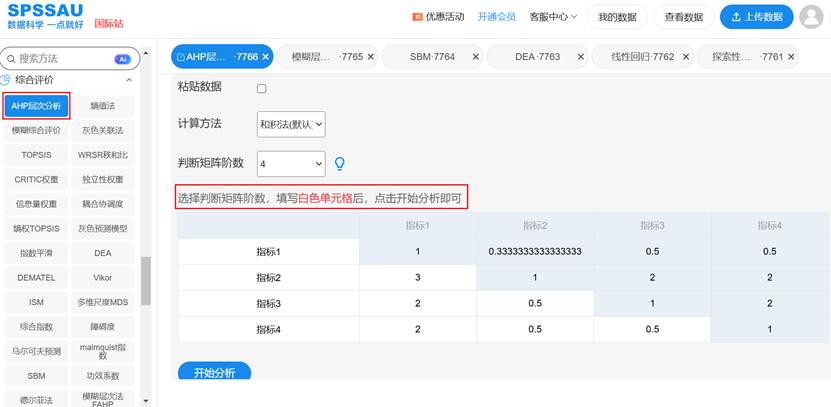
判断矩阵是AHP分析的基础，它体现了决策者对各项指标相对重要性的专业判断。该矩阵具有三个重要特性：对角线元素均为1（指标与自身比较重要性相等）、矩阵互为倒数对称（若A对B的重要性为x，则B对A的重要性为1/x）、数值大小反映相对重要性程度。SPSSAU分析时选择计算方法（和积法或方根法）、选择判断矩阵阶数、填写白色单元格，点击开始分析按钮即可，操作示例如下：

（2）层次分析结果表

呈现了AHP分析的核心产出。特征向量表征了各指标在系统中的相对影响力，权重值则将这种影响力转化为百分比形式，使得各指标重要性一目了然。最大特征值是判断矩阵的一个重要数学特征，为后续的一致性检验提供基础。

（3）一致性检验

是确保判断矩阵逻辑合理性的关键步骤。CI值衡量判断矩阵偏离一致性的程度，RI值为随机一致性指标，CR值（CI/RI）则是最终的检验标准。当CR值小于0.1时，认为判断矩阵具有满意的一致性，权重计算结果可信。SPSSAU直接给出一致性检验结果。

二、FAHP模糊层次法：处理不确定性决策的利器

2.1 FAHP分析流程详解

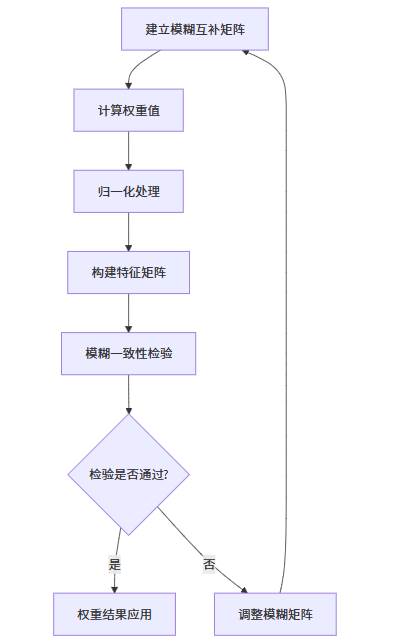
FAHP在传统AHP基础上引入模糊数学理论，更好地处理人类判断中的不确定性和模糊性。上图展示了FAHP的分析流程：从构建模糊互补矩阵出发，通过数学变换计算初始权重，经过归一化处理后得到最终权重，同时构建特征矩阵并进行模糊一致性检验，确保结果的合理性。

2.2 FAHP核心表格解析

（1）模糊互补矩阵

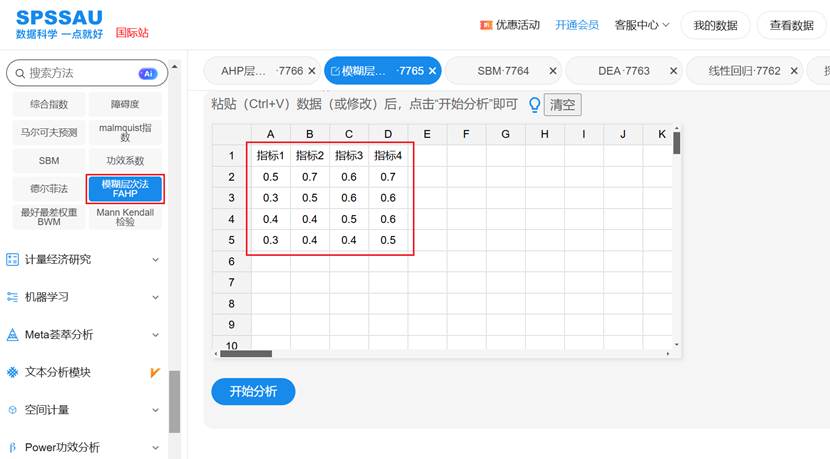
模糊互补矩阵是FAHP分析的起点，采用0.1-0.9标度表示指标间的相对重要程度。与AHP的判断矩阵不同，模糊互补矩阵的对角线元素均为0.5，表示指标与自身同等重要；对称位置的两个值之和恒为1，体现了模糊判断的互补特性。SPSSAU进行模糊层次分析法操作示例如下：

（2）数据标度表格

提供了模糊判断的量化标准。从0.5的"同等重要"到0.9的"极端重要"，构成了一个完整的模糊判断尺度。值得注意的是，0.1-0.4标度作为反比较标度，体现了模糊判断的非对称性。

（3）FAHP权重结果表

展示了模糊层次分析的最终产出。权重值反映各指标在模糊环境下的相对重要性，归一化处理确保所有权重之和为100%，便于实际应用中的解释和比较。

（4）特征矩阵

是FAHP一致性检验的基础，通过权重值计算得出，其元素表示两指标权重之比经特定数学变换后的结果。这个矩阵为模糊一致性检验提供了数学基础。

（5）一致性校验表

是FAHP分析的质量控制环节。与AHP类似，FAHP也需要通过一致性检验来确保判断的合理性，CR值小于0.1是通用的通过标准。

三、AHP与FAHP：方法对比与选择指南

3.1 判断矩阵与模糊矩阵的核心差异

AHP的判断矩阵和FAHP的模糊矩阵虽然都用于表示指标间相对重要性，但在理论基础和表现形式上存在本质区别：

AHP判断矩阵建立在精确数学基础上，要求决策者能够给出明确的数值判断，如1/3、1/5等，体现了"非此即彼"的精确思维。而FAHP模糊矩阵则建立在模糊数学基础上，允许决策者使用0.6、0.7等模糊值表达判断，更符合人类思维中的"亦此亦彼"特性。

在一致性检验方面，AHP采用特征根法进行精确的一致性检验，而FAHP的模糊一致性检验则基于模糊数学理论，对模糊判断的一致性进行评估。

3.2 方法选择的情景分析

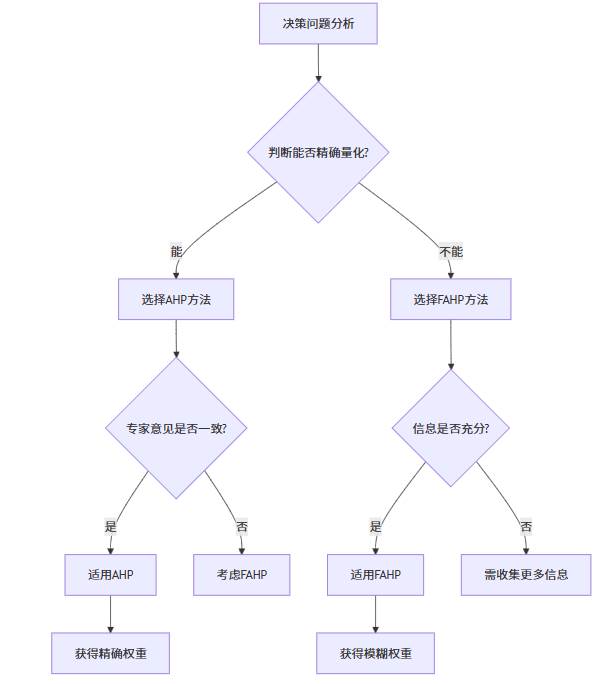
选择AHP还是FAHP取决于决策问题的特性和可用信息的质量。当决策环境稳定、指标关系明确、专家意见一致时，AHP能够提供精确的权重结果；当决策环境复杂、存在不确定性、专家判断具有模糊性时，FAHP则更为适合。

在实际应用中，两种方法并非互斥，而是可以相互补充。研究者可以同时使用两种方法进行分析，通过对比结果增强决策的稳健性。

结语

AHP和FAHP作为经典的权重分析方法，各自适用于不同的决策场景。AHP提供了精确的权重计算框架，适用于信息完备、判断明确的决策环境；FAHP则通过引入模糊数学，更好地处理了现实决策中的不确定性和模糊性。

SPSSAU智能分析平台的出现，使得这些复杂的分析方法变得简单易用，大大促进了权重分析方法在科研和实践中的推广应用。无论你是学术研究者还是商业分析师，掌握这些方法都将在复杂的决策环境中为你提供科学的分析工具和系统的思维方式。