一文讲透 DOE（实验设计）：析因设计、响应面分析与质量优化的系统方法

一、什么是 DOE（土壤为什么“试验设计”？）

在传统实验或调参过程中，我们常常习惯“一次只变一个参数”（One-Factor-At-a-Time, OFAT）：比如先改变温度，观察产出；再改变 pH，观察产出。这样直观，但存在重大局限：如果多个因素同时影响结果，且这些因素之间可能存在交互作用，OFAT 很容易漏掉这些复杂关系。

而 DOE 提供了一种更系统、更高效、更有统计效力的方法。简言之，DOE 是一种通过有计划地设计、执行和分析实验，以最优（或至少高效）地揭示多个输入因素（因子、Factor）如何共同影响一个或多个输出变量（响应、Response）的方法。

• 因子（Factor）：你认为可能影响结果的输入变量／条件（如温度、时间、材料类型、浓度……）
• 水平（Level）：每个因子可能取的设定值或状态（例如温度：25℃ / 35℃，材料：A / B / C）
• 响应（Response）：你关注的输出／结果指标（如产量、纯度、缺陷率、硬度、效率……）

通过设计合理的实验组合（即多个因子的多个水平的组合），DOE 能以远比 OFAT 更少的实验次数，获取关于主效应、交互效应，或非线性（如二次）效应的重要信息。

此外，正确构造的 DOE 可显著降低实验成本、节省时间、提升分析的可靠性和结论的可信度。

二、DOE 的主要类型及其适用场景

基于不同目的和复杂性，DOE 不仅有一种形式，反而是一套涵盖多种设计思想的“工具箱”。下面是最常见、最实用的几类设计。

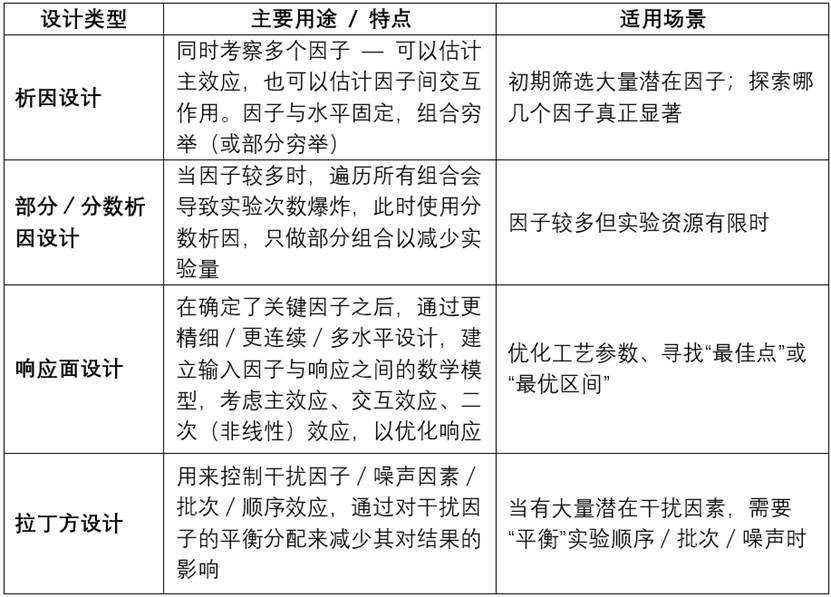
在这一分类体系中：

• 析因设计适合“因子筛选”，尤其是主效应 + 交互效应分析。
• 响应面设计适合“参数优化”场合，可建立可预测模型（线性、带交互、含二次项）并找到最优设定。
• 拉丁方或类似设计则用于“控制噪声／干扰因子” — 保障实验结果的稳健性。

为什么选择不同设计？

• 若你只是想快速筛出哪些因素“可能重要” → 析因／分数析因；
• 若你已经缩减到少数关键因子，需要“调优参数以达到最优” → 响应面设计；
• 若你关注批次／顺序／噪声／干扰因素的平衡 → 拉丁方或其他阻断／区组设计。

三、DOE 的标准流程（逻辑与步骤）

下面是一个典型的 DOE 实施流程 — 以“筛选 → 建模 → 优化”为主线。

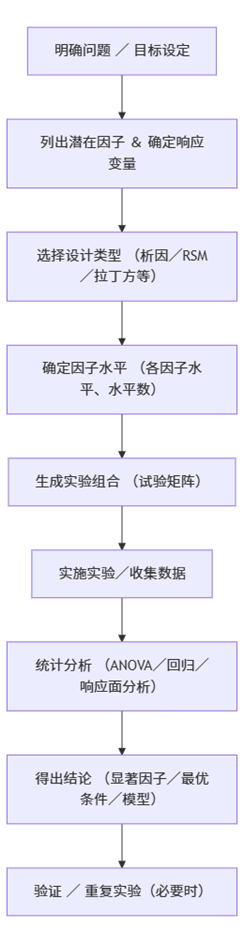
说明：

• A → B：先明确你希望解决的问题／优化的目标，比如“提高产量”、“降低缺陷率”、“优化硬度”等。然后罗列所有可能影响响应的因子（输入变量），以及你希望观察的输出（响应变量）。
• B → C → D → E：基于目标和因子数量，选择最合适的设计类型；然后为每个因子设定合理的水平数／水平值；最后生成一个实验矩阵（试验组合表格），这就是你将要实施的实验方案。
• E → F：严格按照实验矩阵执行实验／测试，并记录响应结果。
• F → G：用统计分析方法（例如方差分析 ANOVA、回归分析、响应面分析等）分析结果，判断哪些因子／交互／二次项对响应显著。
• G → H：根据分析结果，得出结论——哪些因子对响应重要？最佳条件／设定是什么？有没有需要进一步验证？
• H → I：通常需要对“最优条件”进行额外实验验证，确保模型和结果可靠／稳定。

这样一个流程框架，使 DOE 不再是“随便试试”，而成为一个严谨、可重复、可解释、可优化的科学实验过程。

三、为什么越来越多人选择用 “软件 + DOE”

虽然理论上 DOE 可手工设计／编排／分析，但对于实际工程／工艺／质量管理／产品开发来说，手工极易出错、费时费力。另一方面，使用合适的软件工具，则可以大大加速设计、分析和决策过程。

正是在这种背景下，SPSSAU 推出了它的 “质量控制”模块 中的 DOE 实验设计功能。对于工程师、质量管理人员、产品开发者、工艺设计师、科研人员来说，这意味着：

• 更方便快捷生成试验矩阵：不用手动列表、组合；软件能自动按照你设定的因子、水平、设计类型（析因、响应面、拉丁方等）生成试验表格。
• 自动统计分析 + 可视化支持：实验完成后，SPSSAU 可协助进行统计分析（如方差分析 ANOVA、响应面分析、显著性检验等），并输出表格／图形结果，方便你直观理解因素对响应的影响。
• 适用多种常见 DOE 设计：包括 2-水平全析因、部分析因、PB 设计（Plackett-Burman）、以及响应面设计（如 Box–Behnken design, Central Composite Design）等。
• 节省时间与减少人为错误：尤其当因子较多、水平复杂、数据量大时，用软件设计与分析比人工／Excel 高效且稳健得多。

因此，如果你有意提升产品或流程质量、优化参数、做工艺改进／优化，SPSSAU 的 DOE 是一个非常现实、可落地的工具选项 — 它把统计学与质量工程之间的“桥梁”搭起来，让非统计专业背景的人也能相对轻松地开展 DOE 实验。

四、一个较完整的 DOE 应用示例

假设你在一个制造过程中，希望优化“产品硬度”这一指标（Response），你怀疑以下三个因素可能相关：

• 原材料配比 A:B 的比例（Factor 1）
• 混合时间（Factor 2）
• 烘烤温度（Factor 3）

你设定每个因子为两个水平：

• 原材料配比：50:50 / 60:40
• 混合时间：10 min / 20 min
• 烘烤温度：180℃ / 200℃

目标是确定：这些因子／组合是否显著影响硬度，以及是否存在交互效应。

这种情况下，你可以使用 2-水平全析因设计（Full Factorial 2³ = 8 组实验）。

执行这 8 组实验（若资源允许，可以重复多次／每组重复若干次以提高统计效能），并记录每组的硬度测量值。然后通过软件进行 ANOVA 分析：

• 看哪些主效应（配比、时间、温度）显著；
• 是否有交互效应（例如配比 × 温度，或时间 × 温度）；
• 最终判断：哪种组合／设定最优？是否存在稳定的“最优条件”？

如果你发现配比与温度有强烈交互作用，而烘烤温度对硬度敏感，则可能指导你选择 60:40／200℃，或进行更进一步的响应面设计，以微调参数取得最好硬度 + 成本／效率平衡。

用 SPSSAU 做这样的实验设计 + 分析，只需在「质量控制 → DOE 实验设计」模块定义三个因子与两个水平，然后选择 2-水平全析因／析因设计，SPSSAU操作页面示例如下：

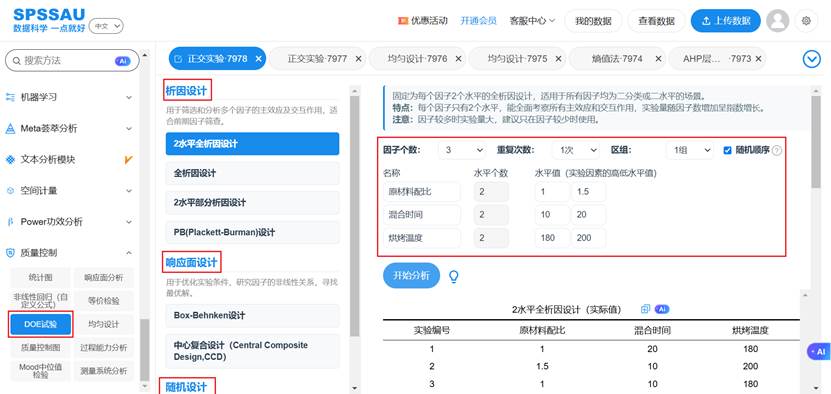
SPSSAU给出分析结果如下：

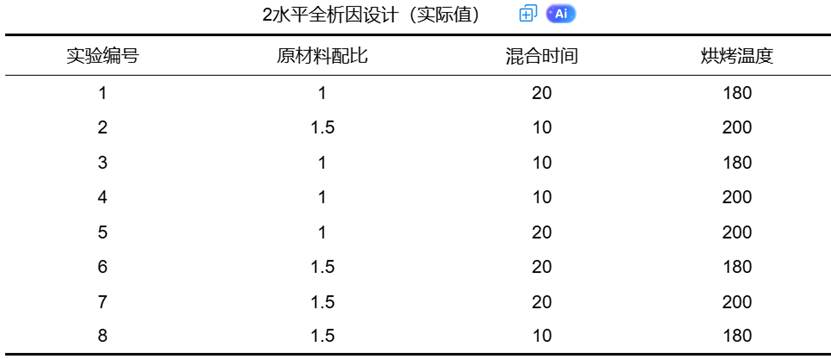
五、DOE 优点、限制与注意事项

1、优点

• 高效 —— 相较 OFAT，DOE 能在更少实验次数下获取更多信息，尤其是对交互／复合效应的识别。
• 系统性强 —— 全面考虑多个因子、多个水平，不只是“随手试试”。
• 结果可靠、可重复、可统计推断 —— 通过设计 + 随机化 + 重复 + 统计分析，结论更具说服力与稳健性。
• 适应复杂系统 / 多因素环境 —— 特别适合产品开发、工艺优化、质量工程、制造／材料研究等复杂场景。

2、限制与必须注意的地方

• 设计／分析复杂 —— 对于非统计背景的人，一开始可能不容易理解交互效应、二次项、响应面模型、假设检验等概念。
• 实验资源要求 —— 全析因设计随着因子数／水平数指数增长，实验次数可能爆炸，耗费时间与资源。
• 模型假设与可解释性 —— 响应面模型往往假设响应是平滑、连续的；若系统非常非线性、杂讯大，模型可能不稳或不适用。
• 对“干扰因素 / 随机误差 /批次效应”等敏感 —— 如果不加控制（随机化 / 均衡 /重复 /阻断），结果可能偏差。

因此，选择合适的设计类型，并严格按照统计原则执行、分析，是保证 DOE 有效与可靠的关键。

六、为什么将 DOE 与 SPSSAU 结合，是现代质量／工艺／产品研发的趋势

在现代制造／产品研发／工艺优化中，我们往往面对多个潜在影响因素（原料、温度、时间、顺序、批次、混合方式……），这些因素相互交互、共同决定最终产品质量或指标。在这种多维、多因素、多变量的环境里，DOE 是理想的方法论。

但传统 DOE 的“人工 + 纸上 + Excel + 手工分析 + 手画图 + 推断”模式，对资源、统计基础要求高，且流程繁琐，容易出错、不便重复或共享。

借助像 SPSSAU 这样的现代统计／数据分析软件，可以让“高阶统计方法”“工业／产品实践”与“质量工程／过程控制”之间产生桥梁，显著降低门槛 —— 让更多非专职统计学背景的人，也能用上 DOE，从而提升质量、降低实验成本、加快优化速度。

这对个人／中小团队／传统制造／快速迭代产品研发／质量管理都有现实价值：不需要采购复杂、昂贵的商业统计软件，也不需要雇专职统计分析人员，就可以做系统、规范、可控的实验设计。

因此，把 DOE + SPSSAU 模块纳入你的质量控制／工艺优化／产品研发流程，是一种值得推荐的“现代实践方式”。

七、总结

DOE 是一种系统化、统计学驱动的实验设计方法 —— 能高效、可靠地揭示多个输入因子对输出响应的影响，尤其适合复杂、多维、多因素场景。

DOE 并不只有一种形式，而是包含析因设计、响应面设计、拉丁方设计等多种设计方案，应根据研究目的（筛选、优化、噪声控制等）选择最合适的一种。

一个标准的 DOE 流程包括：明确目标 → 选择因子 & 响应 → 设计实验矩阵 → 执行实验 → 收集数据 → 统计分析 → 得出结论 → 验证 / 重复。

使用专业统计／数据分析软件（如 SPSSAU 的“质量控制 / DOE 设计模块”）能够极大降低 DOE 的门槛和工作量，将其从“统计学家的工具”转化为“工程师／研发／质量管理者易上手、实用的手段”。

对于产品质量优化、工艺调优、流程改进、成本控制、新产品开发等实际问题，DOE + 软件工具组合，是一种兼顾效率、成本、统计效力和可重复性的现代化方案。