一键理解线性回归：从统计原理到自动化分析实践

最新推荐文章于 2025-12-09 19:50:25 发布

原创最新推荐文章于 2025-12-09 19:50:25 发布 · 619 阅读

CC 4.0 BY-SA版权

文章标签：

在数据分析中，线性回归（Linear Regression）是最基础也是最常用的模型之一。它不仅用于揭示变量之间的线性关系，也构成了众多高级模型（如逻辑回归、结构方程、机器学习回归模型）的理论基础。然而，对很多研究者或数据分析师而言，线性回归的完整过程涉及多个环节——从数据预处理、模型拟合、诊断检验，到模型解释。

本文将系统梳理线性回归分析的核心逻辑与指标体系，并展示如何在 SPSSAU 统计平台中高效完成这一系列分析。

一、线性回归分析的基本流程

线性回归的目标是通过自变量集 X₁, X₂, ..., Xₖ 来预测或解释因变量 Y。

分析流程通常包括以下几个阶段：

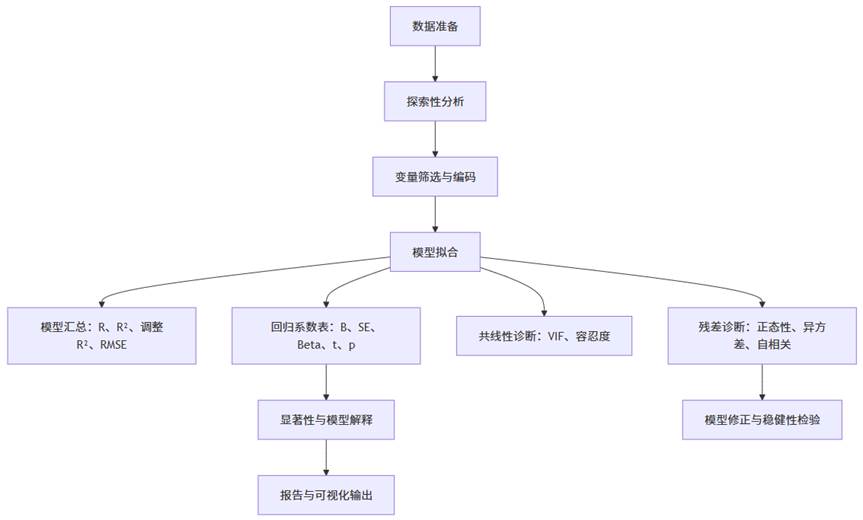
在 SPSSAU 等自动化分析平台中，上述步骤已被整合为可视化流程，一键即可生成模型结果与诊断图表。

二、模型拟合指标：解释模型的整体表现

模型拟合指标用于衡量模型对因变量变异的解释能力。核心包括：

指标	理论含义	解释重点
R / R²	自变量集对因变量变异的解释比例。	越高代表模型解释力越强。
调整 R²	考虑自变量个数后的 R² 校正值。	便于不同模型间比较。
RMSE	残差平方和均值的平方根。	衡量模型的预测误差大小。
AIC / BIC	综合考虑拟合度与复杂度的信息准则。	用于模型选择与优化。

R / R²：自变量集对因变量变异的解释比例，越高代表模型解释力越强。
调整 R²：考虑自变量个数后的 R² 校正值，便于不同模型间比较。
RMSE：残差平方和均值的平方根，衡量预测误差。
AIC / BIC：综合考虑拟合度与复杂度的信息准则，用于模型选择。

三、回归系数与显著性：理解变量的作用方向与强度

每个自变量的回归系数（Coefficient）反映其与因变量之间的线性关系。

指标	理论意义	分析要点
B（非标准化系数）	当自变量增加一个单位时，因变量平均变化的量。	用于实际解释（保留原始量纲）。
Beta（标准化系数）	以标准差为单位的系数。	比较不同自变量的相对影响力。
标准误（SE）	系数估计的不确定性。	与 t 值配合判断显著性。
t 值 / p 值	检验系数是否显著不同于 0。	p < 0.05 通常视为显著。
置信区间（95% CI）	系数估计的可信范围。	反映估计的稳定性。

B（非标准化系数）：当自变量增加一个单位时，因变量平均变化的量。
Beta（标准化系数）：以标准差为单位的系数，用于比较不同变量的相对影响力。
标准误（SE）：系数估计的不确定性。
t 值 / p 值：检验系数是否显著不同于 0。
置信区间（CI）：系数估计的可信范围。

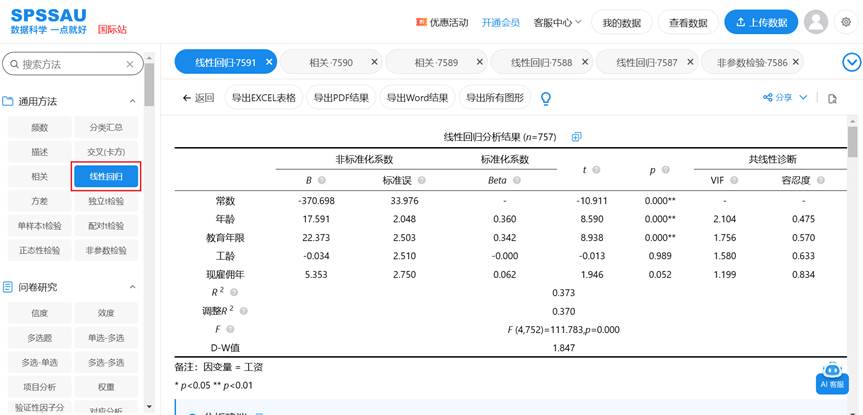
SPSSAU 的报告中会以表格形式呈现这些结果，并自动标注显著性水平（如 p<0.05），便于科研汇报与论文撰写。SPSSAU分析结果页面示例如下图：

四、共线性与残差诊断：模型质量的“体检报告”

好的回归模型不仅要“解释得好”，还要“结构合理”。这就需要对共线性、多重假设和残差行为进行诊断。

指标	理论意义
VIF（方差膨胀因子）	表示共线性导致系数方差膨胀的倍数。VIF>10 通常认为共线性较严重。
容忍度（Tolerance）	1/VIF，表示独立信息量的比例。

共线性（Collinearity）：当自变量之间高度相关时，会导致估计不稳定。

VIF（方差膨胀因子）用于衡量共线性程度；
容忍度（Tolerance）= 1/VIF。

残差检验（Residual Diagnostics）：

线性回归假设残差具有独立、同方差、近似正态的特性。

正态性检验、异方差检验、Durbin–Watson 值都是常用诊断手段。

检验	含义	常见处理方式
正态性检验	检查残差分布形态。	若偏离可使用变换。
异方差检验	检查残差方差是否随预测值变化。	若存在可使用稳健标准误。
Durbin–Watson (D-W)	检验残差自相关性。	若存在序列相关可用自回归模型。

五、从诊断到修正：模型优化的决策路径

当诊断结果显示模型存在问题时，需要根据问题类型采取不同策略：

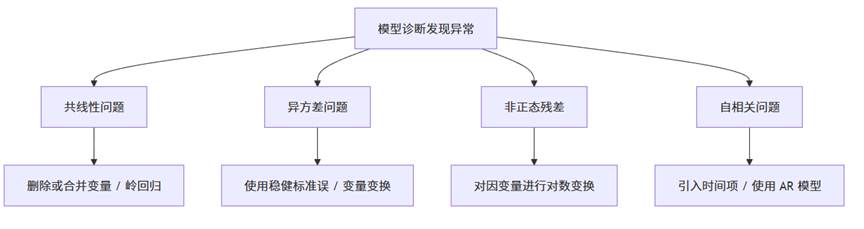
共线性问题 → 删除或合并变量 / 岭回归/lasso回归/主成分回归等。
异方差问题 → 使用稳健标准误 / 变量变换。
非正态残差 → 对因变量进行对数变换。
自相关问题 → 引入时间项或使用自回归模型。

SPSSAU 提供相应的工具选项，例如切换岭回归、自动稳健标准误计算等，使模型优化更高效。但无论使用哪种软件，统计判断始终是核心：模型改进必须遵循理论逻辑与数据特征。

六、可视化与结果呈现

线性回归结果可通过图形直观呈现：

- 回归拟合图（带置信区间的散点回归线）；

- 残差散点图（检测异方差）；

- QQ 图（检验正态性）；

可使用SPSSAU 【可视化】模块生成可视化图形，并支持一键导出 Word 或 PDF 文件，方便科研汇报或课程教学使用。

七、结语：线性回归的思维逻辑

线性回归不仅是一种统计工具，更是一种思维方式。它强调变量之间的线性关系、控制条件与因果推理。通过科学的模型构建与诊断过程，我们可以从数据中提取可靠的结论。无论使用何种分析平台，核心都是一致的：“从理论出发，以数据为证，建立模型，验证假设。”SPSSAU 让这一过程更高效、更可视化，让研究者能把更多精力放在问题思考而非技术操作上。