T检验与方差分析在差异性研究中如何选择？

作为一名科研工作者、数据分析师或者正在为毕业论文奋战的学子，你是否曾在面对两组或多组数据时，感到过一丝迷茫：我到底该用T检验还是方差分析？这两个名字如雷贯耳的工具，看似简单，却在选择上让无数人栽过跟头。

选错了，轻则被审稿人或导师质疑，重则得出完全错误的结论。本文将为你彻底厘清T检验与方差分析的来龙去脉，提供一个清晰、可操作的决策框架，让你在面对差异性研究时，总能做出自信而准确的选择。

一、 T检验与方差分析的核心定义

在深入探讨选择策略之前，我们必须先理解这两个工具的本质。

1. T检验

T检验，顾名思义，其核心是构建一个服从t分布的统计量（t值），用于比较两组数据的平均数是否存在显著差异。你可以把它想象成一场精准的“单挑”或“双人对决”。

它主要解决以下两类问题：

• 单样本T检验：你的样本数据平均值，是否与某个已知的总体平均值存在显著差异？例如，你改进了一种生产工艺，想知道新工艺生产出的产品平均重量（样本均值）是否等于标准重量（总体均值）。
• 独立样本T检验：这是最常见的形式。比较两个独立的、没有关联的组的平均值。例如，比较男性和女性的工资收入；比较A/B测试中，对照组和实验组的用户转化率。
• 配对样本T检验：比较同一组对象在两种不同条件下的差异。例如，比较同一批患者服药前和服药后的血压值；比较同一批学生在参加培训前和培训后的考试成绩。

T检验的核心思想是，通过计算两组均值的差，并考虑数据的变异程度（标准差）和样本量，最终得到一个概率值（p值）。如果这个p值小于我们设定的显著性水平（通常为0.05），我们就认为这两组的均值差异不太可能仅仅是由于随机误差造成的，即存在“统计学上的显著差异”。SPSSAU【通用方法】模块提供三类t检验：

2. 方差分析

方差分析，简称ANOVA，它的使命是同时比较三个或三个以上组的平均值是否存在至少一组与其他组不同。它就像一场“团体擂台赛”，先看整个赛场有没有人出来挑战，再决定是否需要一对一单挑。

它的基本原理非常巧妙：将数据的总变异分解为两部分。

• 组间变异：由于不同处理（组别）不同造成的变异。例如，不同施肥方案（组别）对作物产量（观测值）的影响。
• 组内变异：同一组内部，由于随机误差造成的变异。例如，同一施肥方案下，不同地块作物产量的自然波动。

方差分析通过比较“组间变异”与“组内变异”的大小来计算一个F统计量。如果组间变异显著大于组内变异，说明不同组别造成的差异远大于随机波动，我们就认为至少有两个组的平均值是不同的。

这里有一个至关重要的点：方差分析的结果如果显著，只告诉你“至少有两组是不同的”，但它不告诉你具体是哪两组不同。 要找出具体的差异，你需要进行“事后检验”。

二、何时用T检验？何时用方差分析？

现在，我们来到最关键的部分。选择的标准可以归结为以下三个核心问题：

1. 你要比较几组数据？
   • 只有两组 -> 首选T检验。因为它更直接、统计功效更高。
   • 三组或以上 -> 必须使用方差分析。
2. 如果只有两组，它们的关系是怎样的？
   • 两组数据完全独立（如男/女，A/B测试） -> 独立样本T检验。
   • 两组数据是配对或相关的（如前后测量，配对样本） -> 配对样本T检验。
3. 如果是多组（方差分析），你的数据满足前提假设吗？

这第三个问题，是许多初学者忽略的“魔鬼细节”。无论是T检验还是方差分析，其结论的可靠性都建立在数据满足一定前提条件的基础上。

共同的前提假设：

• 正态性：各组数据应近似服从正态分布。当样本量较大时（如每组>30），根据中心极限定理，这一要求可以适当放宽。正态性检验方法有很多种，例如Kolmogorov-Smirnov检验、Shapiro-Wilk检验、Jarque-Bera检验、Anderson-darling检验。也可以使用直方图、P-P图或Q-Q图进行近似正态性检验。
• 方差齐性：各组的方差应大致相等。对于独立样本T检验和方差分析，方差齐性是一个硬性要求，如果不能满足，可能需要使用非参数检验或Welch‘s ANOVA等校正方法。

SPSSAU【方差】分析时可选择【方差齐检验】如下图：

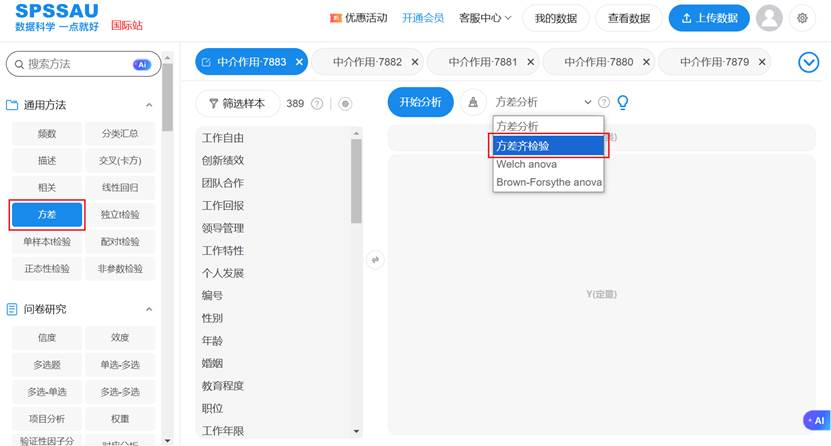
一个经典的错误： 用多次T检验代替方差分析。
比如，你有A、B、C三组数据。如果你想着“我用A比B，A比C，B比C，做三次T检验不就行了？”，那就大错特错了！

这样做会急剧放大“第一类错误”（假阳性）的概率。每次T检验我们允许有5%的概率犯错。但三次独立的检验都不犯错的概率是 (0.95)³ ≈ 0.857，这意味着至少犯一次错的概率飙升到了14.3%！方差分析通过一次整体的检验，完美地控制了这种错误率。